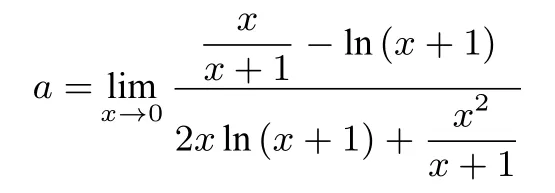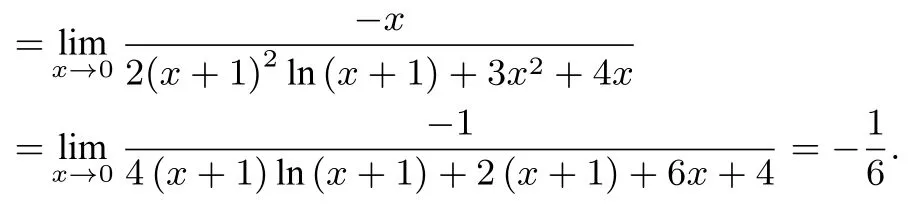已知函数的极值点求参数的取值范围问题的求解策略
2021-06-08广东省中山市中山纪念中学528454李文东
广东省中山市中山纪念中学(528454) 李文东
已知x=x0为函数f(x)的极值点,且f′(x0)=0,求函数f(x)中的参数a的取值范围问题是最近几年全国和各省市高考的热点问题,也是难点问题.比如2016年高考山东卷文科第20 题,2018年高考北京卷第19 题以及2018年全国III 卷的导数压轴题都对此问题进行考查,尤其是全国卷的压轴题,求解难度非常大,以至于部分教师对标准答案颇感费解.经笔者研究,针对此类问题给出常见的求解策略.
策略一:分类讨论,考虑函数的单调性
例1(2018年高考北京卷第19 题) 设函数f(x) =[ax2−(3a+1)x+3a+2]ex.
(Ⅰ)若曲线y=f(x)在点(2,f(2))处的切线斜率为0,求a;
(Ⅱ)若f(x)在x=1 处取得极小值,求a的取值范围.
解(Ⅰ)略.(Ⅱ)f′(x)=(ax −1)(x −1)ex.
(1)当a= 0 时,令f′(x) = (1−x)ex,由f′(x) = 0 得x=1.显然f(x)在(−∞,1)上递增,在(1,+∞)上递减,所以f(x)在x=1 处取得极大值,不合题意.
(2)当a>0 时,令f′(x)=0 得x1=,x2=1.
①当x1=x2,即a=1 时,f′(x)=(x −1)2ex≤0,所以f(x)在R 上单调递增,所以f(x)无极值,不合题意.
②当x1>x2,即0 x (−∞,1)1(1, 1 a)1 a (1 a,+∞)f′(x)+0−0+f(x)↗极大值↘极小值↗ 所以f(x)在x=1 处取得极大值,不合题意. ③当x1 x (−∞, 1 a)1 a (1 a,1)1(1,+∞)f′(x)+0−0+f(x)↗极大值↘极小值↗ 所以f(x)在x=1 处取得极小值,即a>1 满足题意. (3) 当a <0 时,令f′(x) = 0 得x1=,x2= 1.f′(x),f(x)如下表: x (−∞, 1 a)1 a (1 a,1)1(1,+∞)f′(x)−0+0−f(x)↘极小值↗极大值↘ 所以f(x)在x=1 处取得极大值,不合题意. 综上所述,a的取值范围为(1,+∞). 点评极值点问题其本质还是单调性问题,因此只需要分类讨论弄清楚函数的单调性即可,这是解决此类问题的一个基本方法.但是,含参函数单调性的讨论也是导数中的一个难点问题,因此利用分类讨论单调性来求解此类问题往往比较复杂. 例2若x=0 是函数的极大值点,求a的取值范围. 解 因为x= 0 是f(x) 的极大值点,则存在充分接近于0 的δ >0,使得当x ∈(−δ,0) 时,f′(x)>0,当x ∈(0,δ) 时,f′(x)<0.分 析f′(x) 的特点可知,当x ∈(−δ,0) 时,4a2x2−8ax+ 1−6a >0,当x ∈(0,δ)时,4a2x2−8ax+1−6a <0.显然a= 0 不符合要求; 当a ̸= 0 时,y= 4a2x2−8ax+1−6a为开口向上的二次函数,则此时它必然经过原点,于是1−6a=0,得,于是二次函数(x −12),显然x=0 为f(x)的极大值点.综上:a的取值范围为 点评利用极值点的定义,只需要考虑导函数在极值点附近的符号(局部性质),求导后观察分析导函数在极值点附近的符号来确定参数的取值范围. 例3(2018年高考全国III 卷第21 题) 已知函数f(x)=(2+x+ax2)ln(x+1)−2x. (1) 若a= 0,证明:当−1< x <0 时,f(x)<0; 当x>0 时,f(x)>0; (2)若x=0 是f(x)的极大值点,求a. 解(1) 略. (2)f′(x) = (1+2ax)ln(x+1) +−2,则f′(0) = 0,f′′(x) = 2aln(x+1) +则f′′(0) = 0,f′′′(x) =由f′′′(x)=0 得a= 下证:当a=时,x= 0 是f(x) 的极大值点.当可知f′′(x)在(−1,0)单调递增,在(0,+∞)单调递减,进而有f′′(x)≤f′′(0)=0,从而f′(x)在(−1,+∞)单调递减,于是当x ∈(−1,0)时,f′(x)> f′(0) = 0,当x ∈(0,+∞)时,f′(x)< f′(0) = 0,从而f(x)在(−1,0)单调递增,在(0,+∞)单调递减,所以x=0 是f(x)的极大值点.综上:a= 点评极值点的第三充分判别法:已知函数f(x) 在x=x0处各阶导数都存在,若f′(x0) =f′′(x0) =···=f(n−1)(x0) = 0,f(n)(x0)̸= 0,则当n为偶数时,x0是f(x)的极值点(f(n)(x0)>0 为极小值点,f(n)(x0)<0 为极大值点);当n为奇数时,x0不是f(x)的极值点.此种解法借助了高等数学中的结论,已超出了中学数学的知识范畴. 例4题目同例3. 解由题意:x=0 是f(x)的极大值点,则存在充分接近于0 的δ >0,使得当x ∈(−δ,0)时,f′(x)>0,当x ∈(0,δ)时,f′(x)<0,由于对任意的x ∈(−1,+∞),都有2xln(x+1) ≤0,于是有2xln(x+1)+≤0,分离参数后有: ①当x ∈(0,δ)时,a <②当x ∈(−δ,0)时,a >考虑到极值为函数f(x)在x= 0 处附近的性质,让δ →0 并根据洛必达法则有: 评注此题难度极高,以至于中学教师对标准答案也颇感费解,例3 中我们用极值点第三充分判别法解决,但是需要用到较多的高等数学知识,这里的解法相对比较简单,不过也需要用到洛必达法则,对于相关知识点需要给学生补充! 经笔者研究,发现此类问题大部分都可以用分离参数的方法快速统一解决.其一般模式如下: 以x=x0为函数f(x)的极小值点为例,且设f′(x0) =0.根据极小值点的定义可知:存在充分接近于0 的δ >0,使得当x ∈(x0−δ,x0)时,f′(x)<0;当x ∈(x0,x0+δ)时,f′(x)>0.假设f′(x)经过变形后得到:当x ∈(x0−δ,x0)时,a·g(x) (1) 若当x ∈(x0−δ,x0)∪(x0,x0+δ) 时,有g(x)>0(或g(x)<0),则 当x ∈(x0−δ,x0) 时,a <(或a >而 当x ∈(x0,x0+δ) 时a >( 或a <由于δ充分小,故此时实数a的取值范围为:a= (2)若当x ∈(x0−δ,x0)时,有g(x)>0(或g(x)<0),则而当x ∈(x0,x0+δ) 时,g(x)<0(或g(x)>0),则a <由于δ充分小,于是此时实数a的取值范围为:a< 例5(2016年高考山东卷文科第20 题) 设f(x) =xlnx −ax2+(2a −1)x,a ∈R. (1)令g(x)=f′(x),求g(x)的单调区间; (2)已知f(x)在x= 1 处取得极大值,求实数a取值范围. 解(1) 略.(2)f′(x) = lnx −2ax+ 2a,函数f(x)在x= 1 处取得极大值,存在充分接近于0 的数δ >0,使得 当x ∈(1−δ,1) 时,f′(x)>0,当x ∈(1,1+δ)时,f′(x)<0.分离参数后可得:当x ∈(1−δ,1) 时,; 当x ∈(1,1+δ) 时,2a >,从 而即实数a的取值范围为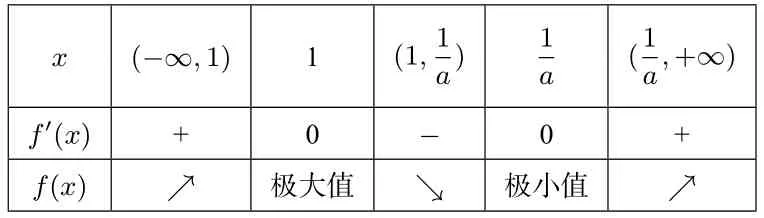


策略二:利用极值点的定义

策略三:利用极值点的第三充分判别法
策略四:分离参数