一道三角形周长最值高考试题的探究与方法应用
2021-06-08北京市第十二中学高中部100071
北京市第十二中学高中部(100071) 赵 毅 刘 刚
1 试题
题目(2020年高考全国Ⅱ卷理科第17 题)∆ABC中,sin2A −sin2B −sin2C=sinBsinC.
(1)求A;
(2)若BC=3,求∆ABC周长的最大值.
试题考查了正(余)弦定理、三角函数的两角和与差公式、三角函数的性质、均值不等式等知识,考查了数学运算、逻辑推理等核心素养,检验了学生分析问题与解决问题的能力,体现了在知识交汇处命题的特点.试题构思巧妙,解法多样,给考生提供了施展才能的舞台,为今后的复习备考指明了方向.
2 解法探究
(1)的解法1因为sin2A −sin2B −sin2C=sinBsinC,
(1)的解法2由sin2A−sin2B −sin2C=sinBsinC,结合正弦定理,得a2−b2−c2=bc,即b2+c2−a2=−bc.由余弦定理,得cosA=因为0< A < π,所以A=
点评在解三角形中,求角问题通常要转化为求这个角的一个函数值.解法1 立足于角,通过三角恒等变换求解;解法2 先借助正弦定理将已知等式转化为边,然后运用余弦定理求解,两种方法各有特色,体现了转化的数学思想.
(2)的解法1由正弦定理,得所以所以
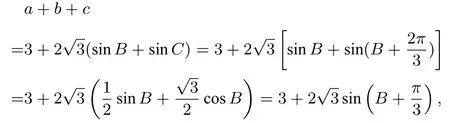
(2)的解法3如图1,延长BA至D,使得AD=AC,连接CD,则AB+AC=BD.由A=所以D=作∆BCD的外接圆O,因为BC= 3,所以点D在优弧上运动(不包括端点),当BD过圆心O时(此时A与O重合),BD最大(这是因为圆中弦为直径时弦长最长),所以(BD)max=故∆ABC周长的最大值为
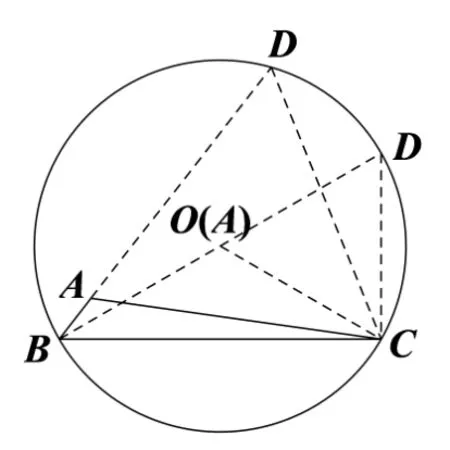
图1
点评解法1 先借助正弦定理,把边转化为三角函数,接下来根据诱导公式、两角和公式进一步转化为一个三角函数,最后借助三角函数的有界性求得最值;解法2 从边入手,根据均值不等式求得最值;解法3 通过添加辅助线,借助平面几何知识求解,体现了过程的简洁性与问题的本质.以上三种方法是处理解三角形中最值问题的常用方法,在应用时,应具体问题具体分析,灵活选用.
对本道试题进行一般化探究,得到:
性质在∆ABC中,角A、B、C的对边分别为a、b、c,记a=m,A=α,则
(1)∆ABC的周长有最大值为
(2)∆ABC的面积有最大值为
3 方法应用
策略一 借助三角函数的有界性
例1(2018年全国高中数学联赛江苏复赛)在∆ABC中,AB= 2AC,且其面积S∆ABC= 1,则BC的最小值是____.
解设∆ABC的内角A、B、C的对边分别为a、b、c,则c= 2b,S∆ABC== 1,所以b2=由余弦定理,得a2=b2+c2−2bccosA= (5−4 cosA)b2=即4 cosA+a2sinA= 5,所以=5(其中锐角φ满足sinφ=由此得解得当且仅当cosA=时等号成立,故BC的最小值是
例2(2013年全国高中数学联赛吉林预赛)已知a、b、c分别为∆ABC三个内角A、B、C的对边,bcosC+a −c=0.
(1)求证A、B、C成等差数列;(2)若b=求2a+c的最大值.
解(1)因为bcosC+−a −c= 0,由正弦定理得到sinBcosC+−sinA −sinC= 0,即sinBcosC+−sin(B+C)−sinC=0,由此得−cosBsinC −sinC=0.因为0
策略二 借助均值不等式
例3(第三十届“希望杯”高二年级一试)在锐角∆ABC中,cosA=则tanBtanC的最小值为____.
解由已知可得tanA=所以tan(B+C) =即
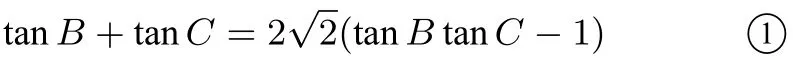
因为∆ABC为锐角三角形,所以tanB >0,tanC >0,所 以tanB+ tanC≤所以①变为两边平方,整理得2(tanBtanC)2−5 tanBtanC+2 ≤0,解得tanBtanC≤2,当且仅当tanB= tanC=时等号成立,故tanBtanC有最小值为2.
例4(2017年全国高中数学联赛一试) 在∆ABC中,M是边BC的中点,N是线段BM的中点.若∠A=∆ABC的面积为的最小值为____.
解由已知,得所以
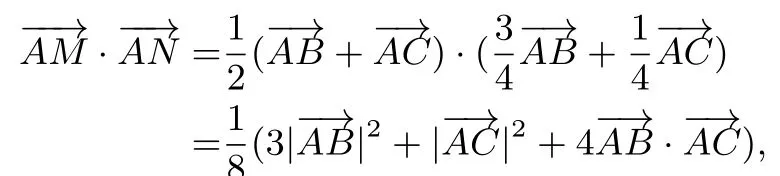
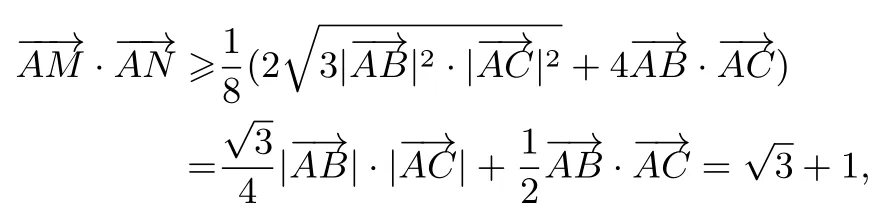
策略三 借助平面几何知识
例5(2018年北京市中学生数学竞赛)一个三角形的一边长为8,面积为12,则这个三角形的周长的最小值为____.
解如图2,在∆ABC中,设BC= 8,BC边上的高 为h,则×8× h= 12,解得h= 3.在BC的一侧作直线l//BC且与BC的距离为3,以l为对称轴作出点C的对称点C′,连接BC′,与l交于A′,则∆A′BC的周长是最小的.这是因为AB+AC=AB+AC′≤BC′=BA′+A′C′=BA′+A′C,此 时A′B=A′C.过A′作A′D⊥BC于D,则D是BC的中点,所以A′B2=BD2+A′D2=42+32=25,即A′C=A′B=5,因此∆ABC周长的最小值为5+5+8=18.
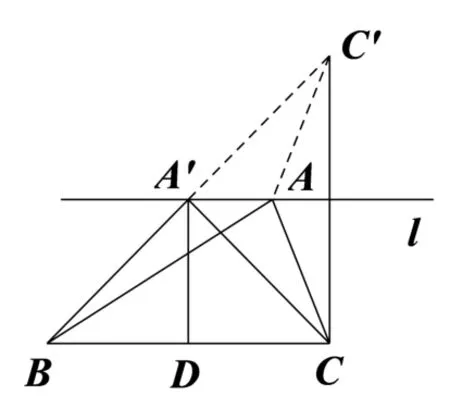
图2
例6在∆ABC中,角A、B、C的对边分别为a、b、c,已知sinA+sinB=求∆ABC面积的最大值.
解如图3,以线段AB的中点为原点,AB所在直线为x轴建立平面直角坐标系,由c= 2,不妨设A(−1,0),B(1,0).又sinA+ sinB=由正弦定理,得a+b=所以点C的轨迹是以A,B为焦点的椭圆(除与x轴交点),于是点C的轨迹方程为= 1(y ̸= 0),所以∆ABC的面积当且仅当点C在椭圆短轴的端点处时等号成立,故∆ABC面积的最大值为
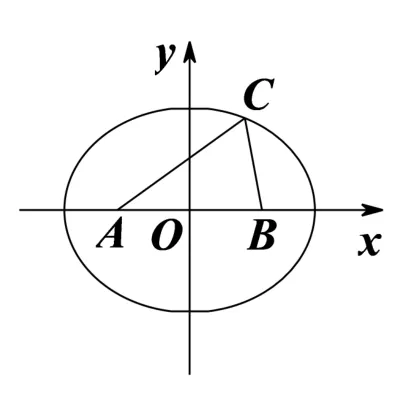
图3
