巧借定点求定值——2020年新高考全国Ⅰ卷第22题的探究

广东省佛山市乐从中学(528315) 林国红

高考试题是精心之作,每年的高考题在命题角度、题型、难度等方面都进行了充分考虑,是知识、能力和思想方法的载体,具有典型性、示范性和权威性.高考试题除了具有测试与选拔功能外,还具有良好的教学功能,要了解高考动向、把握高考脉搏,高考试题的研究是重要的路径.

下面笔者以2020年新高考全国Ⅰ卷(山东卷)第22 题为例,进行分析与解答,并拓展探究,追本溯源,供大家参考.

一、题目呈现与分析

题目已知椭圆C:=1(a>b>0)的离心率为且过点A(2,1).

(1)求C的方程;

(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值.

题目结构清晰,知识方面主要考查椭圆的标准方程和性质,圆锥曲线中的定点定值问题等;思想方面主要考查转化与化归,数形结合等思想.综合考查考生逻辑思维、推理论证及运算求解等方面的能力,试题的思维过程和运算过程体现了能力立意的思想,较好地体现了解析几何中核心内容和基本思想方法的考查.本题作为全卷的压轴题起到了把关作用,对于考生运用所学知识,寻找合理的解题策略以及推理论证和运算能力有较高的要求.

由于问题(1)较为简单,本文不作讨论,下面对问题(2)进行解答与探究.

二、解法探究

证法1设点M(x1,y1),N(x2,y2).当直线MN的斜率存在时,设其方程为y=kx+m,如图1.代入椭圆方程消去y并整理得(1+2k2)x2+4kmx+2m2−6=0.从而有

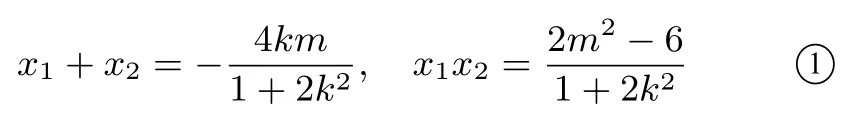
因为AM⊥AN,故=0,故(x1−2)(x2−2)+(y1−1)(y2−1)=0.根据y1=kx1+m,y2=kx2+m,代入整理可得

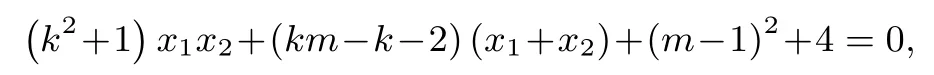
将①代入得到:

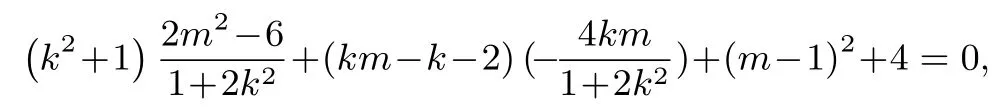
整理化简得(2k+3m+1)(2k+m −1) = 0,因为A(2,1) 不在直线MN上,故2k+m −1̸= 0.所以2k+3m+1 = 0,k ̸= 1,即m=于是MN的方程为所以直线MN过定点

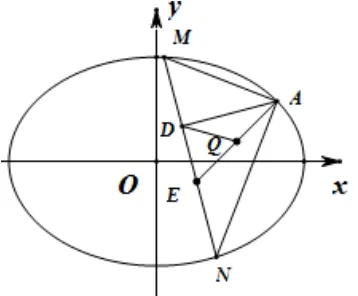
图1

当直线MN的斜率不存在时,可得N(x1,−y1),如图2.因为AM⊥AN,故=0,故(x1−2)(x1−2)+(y1−1)(−y1−1) = 0.结合= 1,可得8x1+ 4 = 0,解得x1= 2(舍),x1=此时直线MN过点由于AE为定值,且∆ADE为直角三角形,AE为斜边,所以AE的中点Q满足|QD|为定值,由于故由中点坐标公式可得所以存在点使得|DQ|为定值,定值为

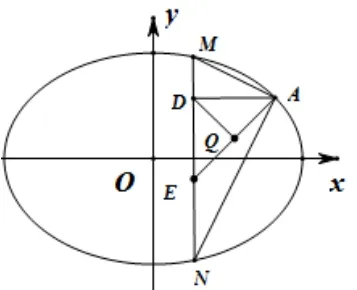
图2

评注(1) 本题的关键是证明出直线MN经过定点再由AD⊥MN,可得点D在以AE为直径的圆上,定点Q为该圆的圆心,|DQ|为该圆的半径,即|DQ|为定值.(2) 本证法的运算量虽不小,但方法是解析几何中的常用方法,这种通性通法在数学解题中有重要作用.所以在平时的教学中要注重一般性的解题规律和方法(即通性通法),要重视知识的生成过程,尽量创设问题情境引导学生探究知识,培养学生分析问题、解决问题的能力.

证法2设直线MN的方程为m(x −2)+n(y −1) =1,点M(x1,y1),N(x2,y2).由= 1,变形得=1,即(x −2)2+2(y −1)2+4[(x −2) + (y −1)] = 0.于是联立直线MN,齐次化得(x −2)2+2(y −1)2+4[(x −2)+(y −1)]×[m(x −2)+n(y −1)] = 0,化简得(2 + 4n)(y −1)2+ 4(m+n)(x −2)(y −1)+(1+4m)(x −2)2= 0,两边同时除以(x −2)2,得

又因kAM · kAN=−1,所以=−1,故n=,代入直线MN的方程为m(x −2)+n(y −1)=1,得m(x −y −1)−= 0.所以直线MN过定点由于AE为定值,且∆ADE为直角三角形,AE为斜边,所以AE的中点Q满足|QD|为定值,由于A(2,1),故由中点坐标公式可得所以存在点使得|DQ|为定值,定值为

评注与两直线斜率相关的定点、定值问题有较强的知识综合性,需要学生具备较高的思维能力与运算能力.齐次化法可以将此类问题统一处理,而且代数变形较为简单,运算量较少,解题过程更为简洁.

三、问题的提出

解答完本题后,思考:

问题1过椭圆C:= 1(a > b >0)上的定点A(x0,y0)作斜率为k1,k2的两条直线分别与椭圆C交于M,N两点,AD⊥MN,D为垂足.若k1k2=−1,是否存在定点Q,使得|DQ|为定值?

问题2在问题1 中,若k1k2=λ(λ为常数),是否存在定点Q,使得|DQ|为定值?

问题3在问题1 中,若k1+k2=µ(µ为常数),是否存在定点P,使得|DP|为定值?

四、借题探究 结论推广

通过探究,可得如下结论:

结论1过椭圆C:= 1(a > b >0)上的定点A(x0,y0)作斜率为k1,k2的两条直线分别与椭圆C交于M,N两点,AD⊥MN,D为垂足.

(1)若k1k2=则存在定点Q,使得|DQ|为定值.

(2)若k1+k2=µ(µ̸=0),则存在定点P,使得|DP|为定值.

证明设直线MN的方程为m(x −x0) +n(y −y0) = 1.由= 1,变 形得= 1,于是= 1,即a2(y −y0)2+[2b2x0(x −x0)+2a2y0(y −y0)]+b2(x −x0)2= 0.于是联立直线MN,齐次化得a2(y −y0)2+[2b2x0(x −x0)+2a2y0(y−y0)]·[m(x−x0)+n(y−y0)]+b2(x −x0)2=0,化简得(a2+2na2y0)(y −y0)2+(2ma2y0+2nb2x0)(x−x0)(y −y0)+(b2+2mb2x0)(x −x0)2=0,两边同时除以(x −x0)2,得b2+2mb2x0=0.于是

(1)当λ ̸=时,由k1k2==λ,即2mb2x0= 2na2y0λ+a2λ −b2,代入直线m(x −x0) +n(y −y0) = 1,整理得(2a2y0λx −2a2x0y0λ+2b2x0y −2b2x0y0)n+ (a2λ −b2)x −a2λx0−b2x0=0,由解得故直线MN过定点由于AD⊥MN,可得点D在以AE为直径的圆上,定点Q为该圆的圆心,|DQ|为该圆的半径,即|DQ|为定值.

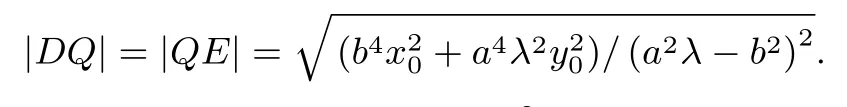
所 以,当k1k2=λ(λ ̸=) 时,则 存 在 定 点使得|DQ|为定值,定值为

(2)当µ̸=0 时,由k1+k2=即−2ma2y0= 2na2y0µ+a2µ+2nb2x0,代入直线m(x −x0)+n(y−y0)=1,整理得(2a2y0µx−2a2x0y0µ+2b2x0x−2b22a2y0y+2a2y20)n+a2µx −a2µx0+2a2y0=0,由解得故直线MN过定点E(x0−由于AD⊥MN,可得点D在以AE为直径的圆上,定点P为该圆的圆心,|DP|为该圆的半径,即|DP|为定值.

因为A(x0,y0),故由中点坐标公式可得且

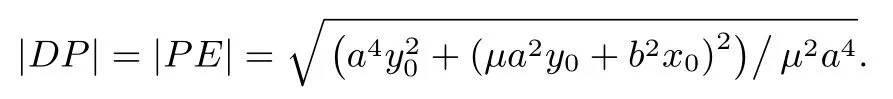
所以,当k1+k2=µ(µ ̸= 0) 时,则存在定点使得|DP|为定值,定 值 为

评注显然,当a2=6,b2=3,λ=−1,且椭圆上的定点为A(2,1)时,由结论1 可知直线MN过定点故存在点使得|DQ|为定值,定值为这正是高考题的情形.

五、拓展探究 类比性质

我们知道,抛物线,椭圆与双曲线都是圆锥曲线,很多时候三者之间有可类比的性质,这体现了圆锥曲线性质的内在统一的和谐美.那么双曲线与抛物线是不是也有类似于结论1 的性质呢? 经探究,得到如下结论:

结论2过双曲线C:= 1(a >0,b >0)上的定点A(x0,y0)作斜率为k1,k2的两条直线分别与双曲线C交于M,N两点,AD⊥MN,D为垂足.

(1)若k1k2=λ(λ ̸=则存在定点Q,使得|DQ|为定值.

(2)若k1+k2=µ(µ̸=0),则存在定点P,使得|DP|为定值.

只需把椭圆E:= 1(a > b >0)中的b2换成−b2,就可以类似地得到双曲线的结论,限于篇幅,这里只给出结论,详细的证明过程不再给出.

(1) 若k1k2=λ(λ ̸=则存在定点使 得|DQ|为定值,定值为

(2) 若k1+k2=µ(µ ̸= 0),则 存 在 定点使 得|DP|为 定 值,定 值 为

结论3过抛物线C:y2= 2px(p >0) 上的定点A(x0,y0)作斜率为k1,k2的两条直线分别与抛物线C交于M,N两点,AD⊥MN,D为垂足.

(1)若k1k2=λ(λ ̸=0),则存在定点Q,使得|DQ|为定值.

(2)若k1+k2=µ(µ̸=0),则存在定点P,使得|DP|为定值.

证明设直线MN的方程为m(x−x0)+n(y −y0)=1.由y2= 2px,变形得(y −y0+y0)2= 2p(x −x0+x0),于是(y −y0)2+2y0(y −y0)+y20= 2p(x −x0)+2px0,即(y −y0)2+2y0(y −y0)−2p(x −x0) = 0.于是联立直线MN,齐次化得

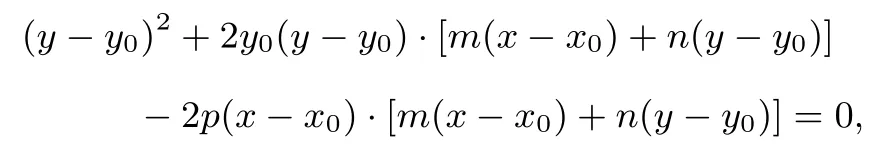
化简得(1+2ny0)(y −y0)2+(2my0−2pn)(x −x0)(y −y0)−2pm(x −x0)2=0,两边同时除以(x −x0)2,得

于是k1+k2=

(1) 当k1k2==λ时,显然λ ̸= 0.可得−2pm=λ+2nλy0,代入直线m(x −x0)+n(y −y0) = 1,整理得(2y0λx −2x0y0λ −2py+ 2py0)n+λx −λx0+2p= 0,由解得所以直线MN过定点由于AD⊥MN,可得点D在以AE为直径的圆上,定点Q为该圆的圆心,|DQ|为该圆的半径,即|DQ|为定值.

(2) 当µ ̸= 0 时,由k1+k2=µ,即−2my0= 2ny0µ −2pn+µ,代 入 直 线m(x −x0) +n(y −y0) = 1,整理得(2y0xµ −2px −2x0y0µ+2px0−2y0y+ 2y20)n+µx −µx0+ 2y0= 0,由解得故直线MN过定点

由于AD⊥MN,可得点D在以AE为直径的圆上,定点P为该圆的圆心,|DP|为该圆的半径,即|DP|为定值.因为A(x0,y0),E(x0−),故由中点坐标公式可得且|DP|=|AP|=所以,当k1+k2=µ(µ̸=0)时,则存在定点使得|DP|为定值,定值为

六、追本溯源

1.(2007年高考山东卷理科第21 题)已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C上的点到焦点距离的最大值为3,最小值为1.

(1)求椭圆C的标准方程;

(2)若直线l:y=kx+m与椭圆C相交于A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点,求证:直线l过定点,并求出该定点的坐标.

2.(2013年四川省高中数学联赛预赛第15 题) 已知B(0,1),P,Q为椭圆+y2= 1 上异于点B的任意两点,且BP⊥BQ.

(1)若点B在线段PQ上的射影为点M,求M的轨迹方程;

(2)求线段PQ的中垂线l在x轴上的截距的取值范围.

3.(2017年福建省高中数学联赛预赛第12 题)已知椭圆C:= 1(a > b >0) 过点P(−2,1),且离心率为过点P作两条互相垂直的直线分别交椭圆于A,B两点(A,B与点P不重合).求证:直线AB过定点,并求该定点的坐标.

可以看出2020年考题问题(2)的“母题”来源于上述高考题或竞赛题,高考题或是将母题进行适当的改编,或是赋于更丰富的知识而已.这说明命题专家很重视命题的传承和相互借鉴.所以在高考的备考中,适当加入高考真题的训练是必要的,特别是近几年的高考真题,另外还可以适当加入一些接近高考难度的高中数学联赛题的训练.

七、反思提升

圆锥曲线中的定点定值问题,是高考或竞赛的热点问题之一,这类问题在考查圆锥曲线基础知识和几何性质的同时,又能很好地考查学生的运算求解、推理论证等数学能力,以及分类讨论和转化与化归等数学思想的理解水平.在解题时要学会探索、归纳和总结,把同类型的问题归于一类,以不变应万变.

圆锥曲线具有很多统一或相似的性质,这些优美的性质深刻反映了数学独特的无穷魅力,值得我们去寻找、发现和欣赏.学数学离不开解题,但不能仅仅局限于老师讲题、学生做题,而是要借助题目,探索隐藏在题目背后的奥秘,将研究的问题引向深入,挖掘题目的真正内涵,能够找到解决这个问题与解决其它问题在思维上的共性.这样我们才能领会到试题命制的深刻背景,才能引领学生跳出题海,真正做到触类旁通,举一反三,从而达到做一题会一类,甚至会一片的目的,最终让学生在解题思路上产生质的变化,使思维得到发展.