基于三次样条插值的小波模极大值去噪算法

赵鸿图，刘 云

（河南理工大学 计算机科学与技术学院，河南 焦作454000）

0 引 言

目前，研究者们在模极大值理论基础上对信号去噪算法提出了许多新的思想和新的改进［1－4］。现主要采用的是传统模极大值直接重构算法和交替投影法，传统模极大值直接重构算法由于对各尺度上一些非模极大值点的小波系数［5，6］都置为零，损失了信号的信息，降低了算法的精度。即使此算法程序简单，去噪速度快，但是重构后的信号失真太大。1992年，Mallat提出了一种很逼近小波系数的精密的交替投影算法［7］，该算法保留了那些非模极大值的点，不会损失掉微弱的有用信号，保证了信号的完整性，经过反复的交替投影，的确达到了很高的精度，但是计算量太大，收敛速度太慢。在文献 ［8］中，韩民等提出了一种基于Hermite插值的小波模极大值重构信号的算法；在文献［9］中，刘跃华等提出了一种抛物线插值的重构算法。

本文在传统模极大值直接重构算法和交替投影法的基础上，提出了一种基于三次样条插值［10］的小波模极大值去噪算法，利用Adhoc算法［11］搜索信号产生的模极大值点，形成模极大值线。对于保留下来的模极大值点进行三次样条插值，得到信号的估计小波系数，进而用估计小波系数重构原始信号，达到滤波去噪的目的。该算法不但确保了信息的完整性，又保证了收敛速度的快捷性。

1 小波模极大值与李氏指数的关系

由于小波基并不是固定不变的，只要满足允许条件即可，其小波的表现形式也不是唯一的。设在尺度s 下，Wf（s，x）是卷积型小波变换，小波变换卷积形式表示为

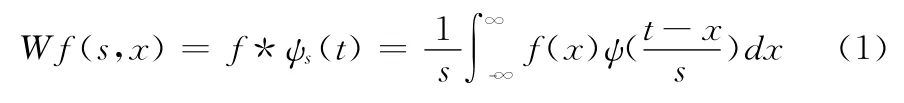
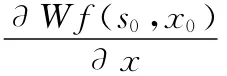
数学上，李氏 （Lipschitz）指数可以用来表示函数的局部正则性。在信号处理中，信号的奇异点表征信号在该处出现了突变或者间断，发生了奇异性改变。所以信号的奇异性包含信号的许多信息，通常采用Lipschitz指数来分析和研究信号突变点的奇异性，其定义如下

设函数f（x）在x0附近有

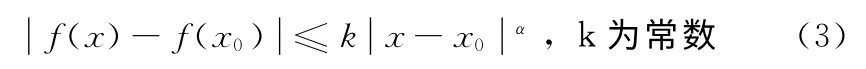
则称f（x）在x0处的李氏指数为α。α越大，该点的光滑度越高；α越小，该点的奇异性越大。当x 在区间［a，b］时，f（x）的小波变换满足

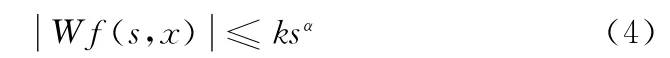
取s＝2j，对式 （4）两边取对数得

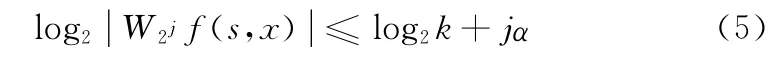
由式 （5）可知，小波模极大值与α有密切关系，若α＞0，f（x）在该点的小波模极大值与尺度j是正增长关系；若α＜0，f（x）在该点的小波模极大值与尺度j是负增长的关系；若α＝0，则该点处的小波模极大值不发生变化。

2 Adhoc算法

Adhoc算法就是通过大尺度上的模极大值点来找到小尺度的模极大值点，以形成模极大值线。本文采用Adhoc算法估计Lipschitz指数，进而获得模极大值线上要传播到下一尺度的模极大值点。虽然Adhoc算法不是最优算法，但是能够抑制模极大值漂移，可以解决错选模极大值传播点的问题，是一种简单有效的算法。Adhoc算法搜索传播点步骤如下：

（1）从最大尺度J开始，往小尺度方向搜索。设x0为尺度J上的一个模极大值点，其前后的2个模极大值点分别为x1和x2，x′1是x1的传播点，则x0在尺度J－1下对应的传播点区间L ＝（max（x1，x′1），x2）。

（2）在尺度j－1下，L 上与x0同符号的点（t1，t2，…，tn）中，若ti满足

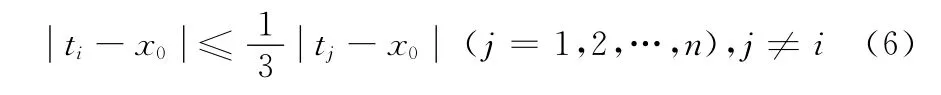
则ti为x0的传播点。

（3）若不存在这样的点，则在L上，如果满足

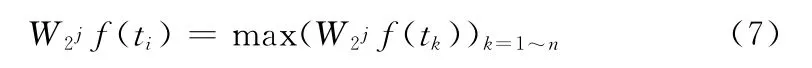
那么点ti为x0的传播点x′0。

（5）重复以上过程，直至尺度j＝2，将搜索的各尺度上的模极大值点xi，x′i，x″i…作为信号极大值线上的点给予保留。

3 基于三次样条插值的小波模极大值去噪算法

为了采用小波模极大值的思想重构信号，提高信号重构的精度，最重要的是找到一个函数使得函数的最大值与小波模极大值相一致。由于三次样条函数的中心对应模极大值点，函数的最大值与模极大值正好吻合，这样不仅解决了模极大值点由于分布稀疏或者稠密而引起的插值区间分布不均的问题，还保证了信号的光滑性，降低了信号的失真度。

3.1 基于三次样条插值的小波模极大值算法步骤

其算法步骤如下：

（1）对带噪信号进行离散二进小波变换，尺度j＝4；（2）求出各尺度上小波变换系数对应的模极大值点；

（3）对最大尺度J上的模极大值点进行阈值处理，如果模极大值点对应的幅值的绝对值小于阈值T，则剔除该极值点；否则予以保留。选取的阈值T 为

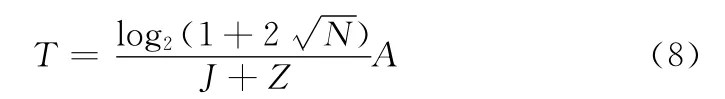
式中：N——噪声功率；J——所取的最大尺度；Z——常数，一般取Z＝2；A——最大模极大值点的幅度。

（4）从最大尺度J开始利用Adhoc算法向上搜索其对应的模极大值线，寻找下一尺度的传播点，直到j＝2，搜索到所有信号模极大值点为止；

（5）将各尺度保留下来的信号的模极大值点采用三次样条函数插值算法估计小波系数，进而重建信号，具体如下：

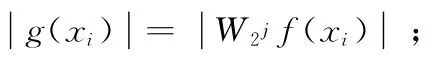
2）在信号区间［a，b］上插入n个模极大值点，a ＝x1＜x2＜… ＜xn＝b，对应的函数值为y1，y2，…，yn，边界条件y′1，y′2，g（x）在［xj，xj＋1］上的三次多项式为

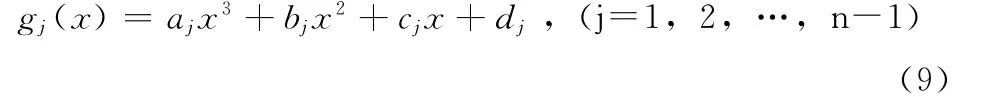
设

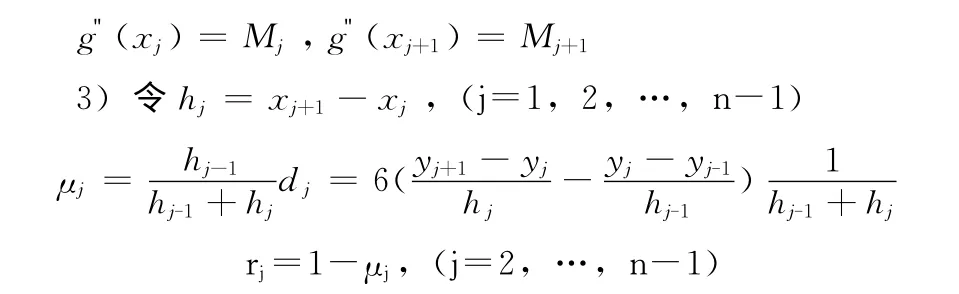
计算

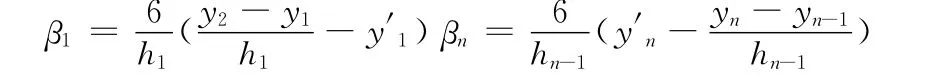
4）将方程组写成矩阵形式

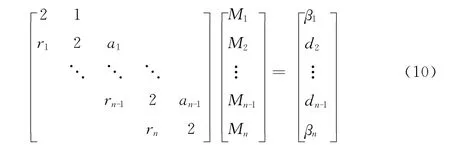
由式 （10）可知方程组的系数矩阵是三对角阵且是对角占优阵，故存在唯一解。将求得解代入下式，即可构造［a，b］上的插值函数，如下所示

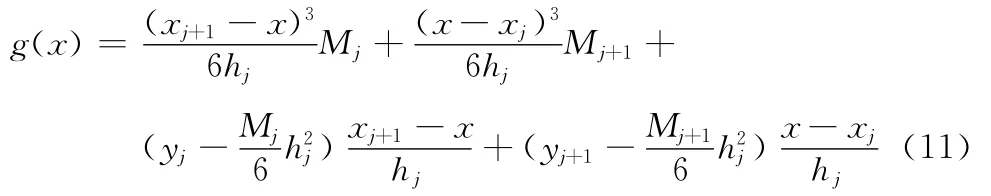
利用式 （11）可以计算出每一尺度上的构造函数，从而得到小波系数重构原始信号，实现滤波去噪的目的。

3.2 算法流程图

其算法流程如图1所示。

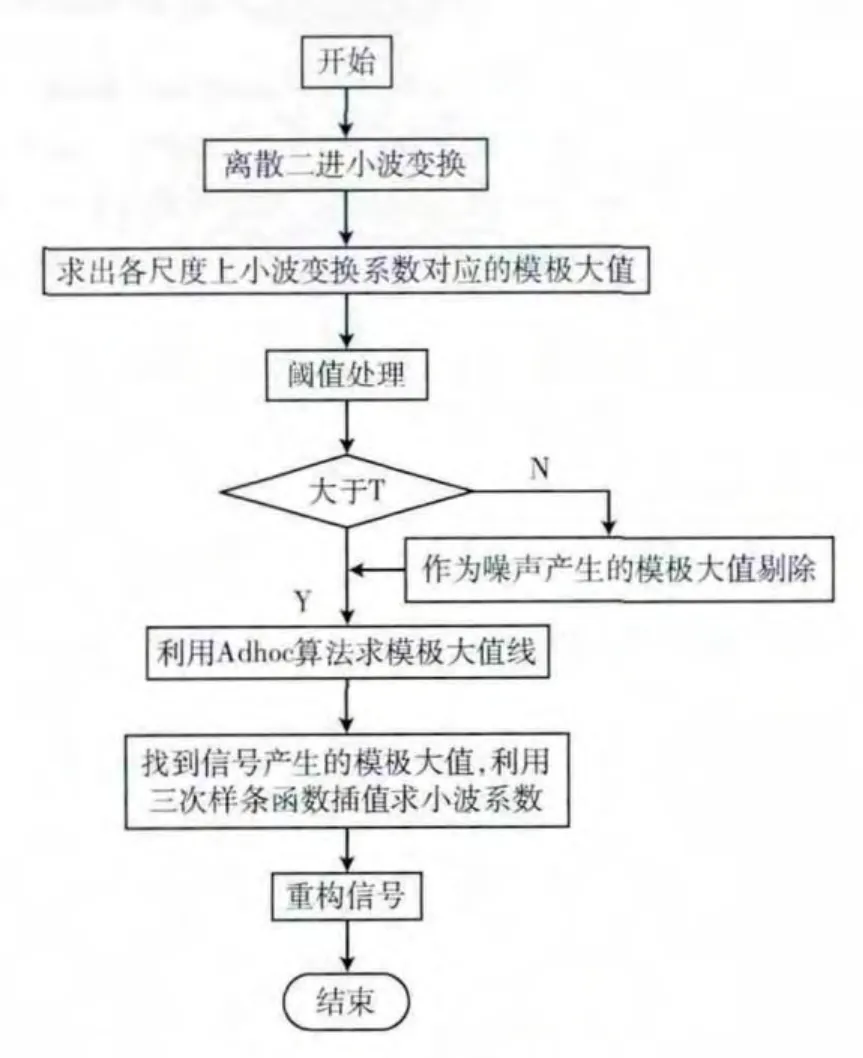
图1 本文算法流程

4 实验仿真结果

在MATLAB 环境下，分别采用交替投影法和本文改进的插值算法对带噪信号进行去噪处理，信号长度为1024，选取db3小波进行4层分解，实验仿真结果如图2～图5所示。

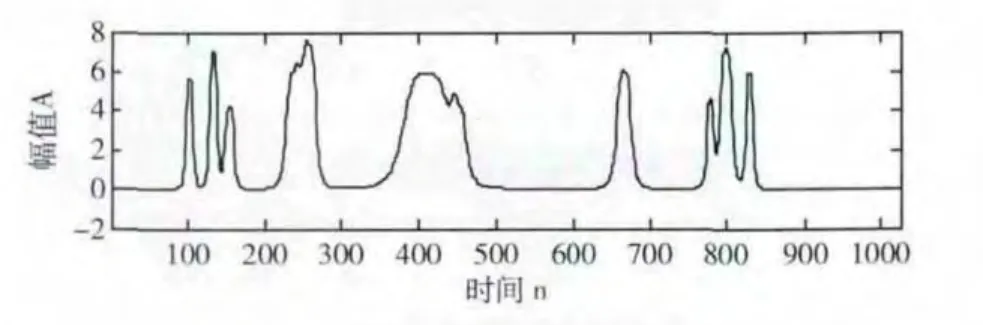
图2 原始信号

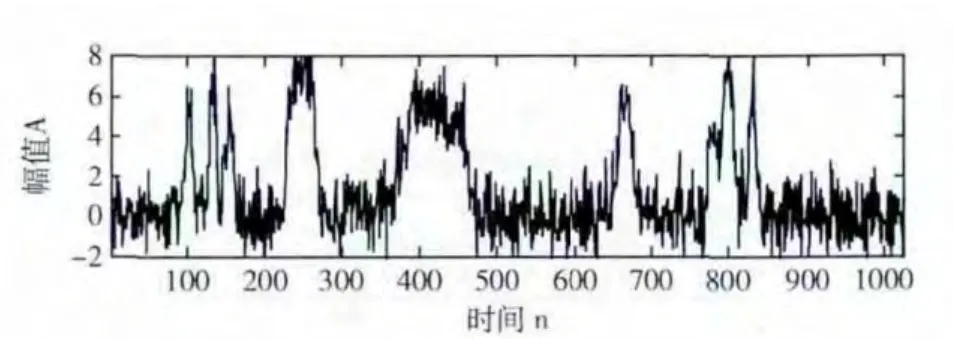
图3 带噪信号

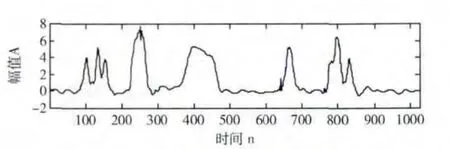
图4 交替投影法重构后的信号

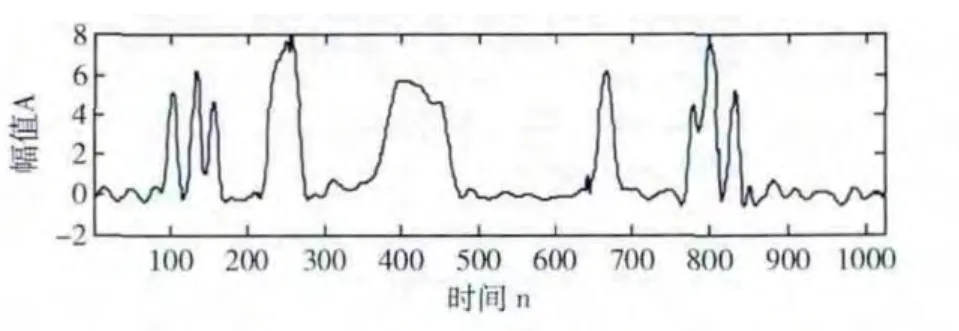
图5 本文改进算法重构后的信号

通过图4和图5比较，我们可以发现，这2种算法都能在一定程度上去除噪声，但交替投影法重构后的信号在许多点上波形发生了变化，例如在788凹口处，本来原信号的幅值在最低值2处，而交替投影法重构后的信号幅值基本保留在幅值4处，该算法去噪的同时也把原来信号的信息去除了，产生了一定的失真；本文改进的算法去噪效果明显优于交替投影法，去噪后的信号不很光滑，却在突变点处保留了信号的重要信息，重构后信号与原始信号基本一致。

通过图6，显而易见，经过2种算法重构后，各层的模极大值点位置有很大的悬殊，交替投影法重构后疏漏了很多模极大值点，例如在j＝2层上，第1个模极大值点疏漏掉了，而且有的地方模极大值点对应的位置也产生了漂移；而本文改进算法重构后基本没损失模极大值点，模极大值点的位置很直观，易于查找，对应的位置也很稳定，大大降低了信号的失真度。

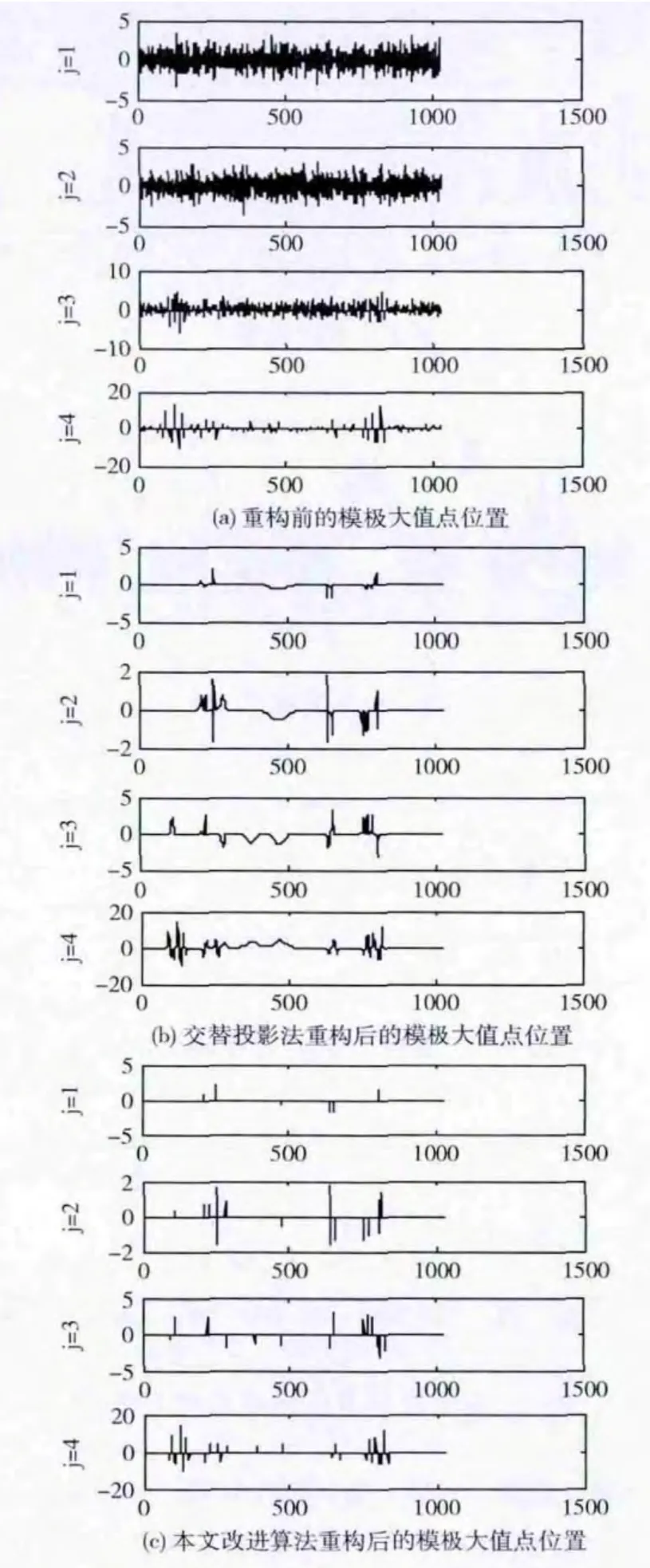
图6 信号的模极大值点位置

经交替投影法和本文改进算法去噪后，信号的信噪比见表1。

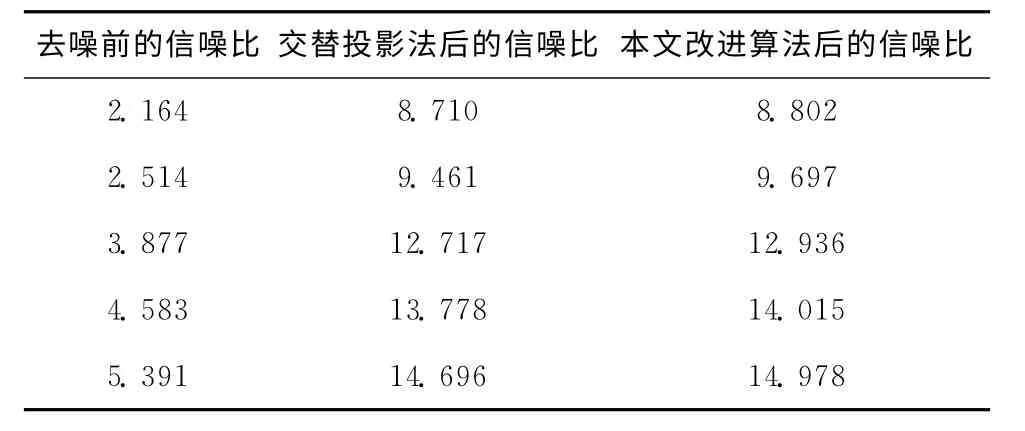
表1 去噪算法的信噪比

从表1中信号信噪比数据来看，2种方法去噪后的信噪比增益都很大，但本文改进算法的信噪比高于交替投影法，性能明显优于交替投影法。

2种算法运算时间的比较见表2。

表2 去噪算法运算时间

从表2中算法运算时间来看，本文改进算法的运算时间比交替投影法快了87ms，收敛速度和去噪性能明显优于交替投影算法。

5 结束语

本文研究了交替投影算法运算量大和收敛速度慢的问题，并提出了一种改进算法，利用三次样条函数对信号模极大值进行插值，得到小波系数，进而重构原始信号。经过仿真结果表明，该改进算法是一种很有效的去噪方法，便于实现，与交替投影法相比，该算法不仅达到了很高的精度，运算量和运算时间也明显减少。但是也存在一些缺陷，比如传播邻域以及插值函数构造问题，这些都需要我们进一步研究。

［1］TIAN Xiurong.Speech de－noise and enhancement using orthogonal wavelet packet decomposition ［J］.Computer Simulation，2011，28 （5）：388－390 （in Chinese）.［田秀荣.基于正交小波包分解的语音去噪增强 ［J］.计算机仿真，2011，28 （5）：388－390.］

［2］WANG Biao，LI Jianwen，WANG Zhongfei.Threshold denoising method based on wavelet analysis［J］.Computer Engineering and Design，2011，32 （3）：1099－1102 （in Chinese）.［王彪，李建文，王钟斐.基于小波分析的新阈值去噪方法［J］.计算机工程与设计，2011，32 （3）：1099－1102.］

［3］LIU Limei，LIU Qiyue，ZHANG Jing.Research in de－noising method based on wavelet transform modulus maxima ［J］.Hebei Journal of Industrial Science and Technology，2010，27（6）：367－372 （in Chinese）.［刘丽梅，刘齐跃，张静.基于小波变换模极大值的去噪方法研究 ［J］.河北工业科技，2010，27 （6）：367－372.］

［4］FENG Ganzhong，HE Zhiming.Wideband rader signal de－noising method based on modulus maximum ［J］.Modern Radar，2013，35 （6）：38－41 （in Chinese）.［冯淦忠，贺知明.基于模极大值的宽带雷达信号去噪方法 ［J］.现代雷达，2013，35：38－41.］

［5］GUO Jiapan.Signal reconstruction based on the wavelet modulus maxima of quadratic programming ［D］.Xi’an Xidian University，2012：12－13 （in Chinese）. ［郭佳盼.基于二次规划的小波模极大值信号重构 ［D］.西安：西安电子科技大学，2012：12－13.］

［6］QIN Yi，WANG Jiaxu，MAO Yongfang.Signal de－noising based on soft thresholding and reconstruction from dyadic wavelet transform modulus maxima［J］.Journal of Vibration，Measurement ＆Diagnosis，2011，31 （5）：543－547 （in Chinese）. ［秦毅，王家序，毛永芳.基于软阈值和小波变换模极大值重构的信号去噪［J］.振动、测试与诊断，2011，31 （5）：543－547.］

［7］Mallat S，Zhang S.Characterization of signals from multiscales edges［J］.IEEE Trans on PAMI，1992，14 （7）：710－732.

［8］HAN Min，TIAN Lan，ZHAI Guangtao，et al.Fast reconstruction algorithm based on Hermite interpolation from modulus maxima of wavelet transform ［J］.Journal of System Simulation，2005，17 （11）：2616－2619 （in Chinese）. ［韩民，田岚，翟广涛，等.基于Hermite插值的小波变换模极大值重构信号快速算法［J］.系统仿真学报，2005，17 （11）：2616－2619.］

［9］LIU Yuehua，ZENG Yingsheng.Simulation of improved denoising algorithm in signal processing ［J］.Computer Engineering and Applications，2009，45 （4）：149－151 （in Chinese）.［刘跃华，曾迎生.信号处理中去噪算法的改进仿真 ［J］.计算机工程与应用，2009，45 （4）：149－151.］

［10］XIE Xiaoyong，LIU Xiaodong，HU Linling，et al.Cubic constrained rational interpolating spline［J］.Computer Engineering and Applications，2010，46 （24）：173－176 （in Chinese）.［谢晓勇，刘晓东，胡林玲，等.一种有理三次样条的约束插值［J］.计算机工程与应用，2010，46 （24）：173－176.］

［11］XI Dongmei.Research on speech enhancement algorithm and implementation of MATLAB ［D］.Jiaozuo：Henan Polytechnic University，2012：18－20 （in Chinese）.［席冬梅.语音增强算法研究及MATLAB 实现 ［D］.焦作：河南理工大学，2012：18－20.］