2021年美国数学竞赛(AMC10A)的试题与解答

2021-06-08华南师范大学数学科学学院510631李湖南

中学数学研究(广东) 2021年9期

关键词：张纸筹码英里

华南师范大学数学科学学院(510631) 李湖南

1.算式(22−2)−(32−3)+(42−4)的值是多少?

(A) 1 (B) 2 (C) 5 (D) 8 (E) 12

解直接计算,原式=2−6+12=8,故(D)正确.

2.Portia 高中的学生人数是Lara 高中的3 倍,这两所高中总共有2600 名学生.问Portia 高中有多少名学生?

解依题意可知,Portia 高中占总人数的即有2600×=1950 名学生,故(C)正确.

3.两个自然数之和是17402.这两个数中的一个可以被10 整除,如果去掉该数的个位数字则得到另外一个数.问这两个数的差是多少?

(A) 10272 (B) 11700 (C) 13362 (D) 14238 (E) 15426

解设第一个数为x,则第二个数为已知x+17402,解得x= 15820,于是两数之差为x −=14238,故(D)正确.

4.一辆小车冲下山坡,它第一秒移动了5 英寸,并且速度不断加快.在每个连续的1 秒时间间隔内,它都比前1 秒多移动7 英寸.小车用了30 秒到达山脚.问它一共行进了多少英寸?

(A) 215 (B) 360 (C) 2992 (D) 3195 (E) 3242

解小车每秒移动的距离是个等差数列,首项为5,公差为7,第30 秒移动了208 英寸,从而距离和为(5+208)×30÷2=3195 英寸,故(D)正确.

5.一个共有k >12 名学生的班级进行测验的平均分为8 分,其中12 名学生的测验平均分是14 分.问其余学生的测验平均分如何用k来表示?

解所有学生的分数总和为8k,其中12 名学生的分数和为168,剩下k −12 名学生的分数和为8k −168,故平均分为(B)正确.

6.Chantal 和Jean 从山路的起点开始向消防塔徒步旅行.Jean 背着一个沉重的背包,走得较慢.Chantal 开始以每小时4 英里的速度行走,走到路程一半,山路变得非常陡峭,Chantal 的速度减慢到每小时2 英里.到达塔后,她立即掉头,以每小时3 英里的速度沿着陡峭的山路向下走,她在路程的一半处遇见了Jean.从出发到他们相遇,Jean 的平均速度是每小时多少英里?

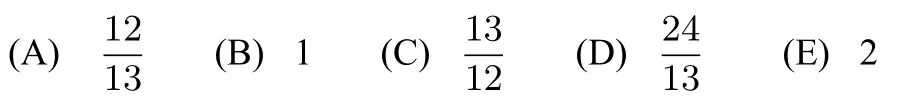
解设半程为x英里,Jean 所用的时间与Chantal 一样,均为小时,于是Jean 的平均速度为英里/小时,故(A)正确.

7.汤姆有13 条蛇,其中4 条是紫色的,5 条是快乐的.他观察发现:他的所有快乐的蛇都能做加法,他的紫色的蛇不会做减法,而且他所有不会做减法的蛇也不会做加法.关于汤姆的蛇,可以得出以下哪个结论?

(A) 紫色的蛇可以做加法 (B) 紫色的蛇是快乐的

(E) 快乐的蛇不能做减法

解紫色的蛇不会做减法,从而也不会做加法,因此也不是快乐的.故快乐的蛇都不是紫色的,(D)正确.

8.一名学生在用66 乘以如下的循环小数时,1.abab···= 1.˙a˙b,其中a和b是数字.他没有注意到循环小数的标识,而只是做了66 乘以后来他发现他的答案比正确答案小0.5.问两位整数是多少?

(A) 15 (B) 30 (C) 45 (D) 60 (E) 75

解由题意可得,0.5=66×(1.˙a˙b−=66×0.00˙a˙b=0.66×,解得=75,故(E)正确.

9.对于实数x和y,(xy −1)2+(x+y)2的最小可能值是多少?

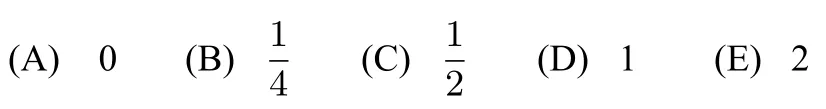
解(xy −1)2+(x+y)2=x2y2+x2+y2+1 ≤1,此时x=y=0,故(D)正确.

10.算式(2 + 3)(22+ 32)(24+ 34)(28+ 38)(216+316)(232+332)(264+364)与下面哪个表达式相等?

(A)3127+2127(B)3127+2127+2×363+3×263

解连续使用平方差公式,可得原式=(3−2)(3+2)(32+22)(34+ 24)(38+ 28)(316+ 216)(332+ 232)(364+ 264) =3128−2128,故(C)正确.

11.选择下面哪个整数b为基数,可以使得b进制数2021b −221b不能被3 整除?

(A) 3 (B) 4 (C) 6 (D) 7 (E) 8

解由于2021b −221b=2×b3−2×b2=2b2(b −1),当b=3,4,6,7 时,该数均能被3 整除,故(E)正确.

12.如图所示,两个顶点朝下的正圆锥包含相同量的液体.液体顶部表面的半径分别为3 厘米和6 厘米.在每个圆锥体中放入一个半径为1 厘米的球形弹子,它沉入底部,完全浸没,没有任何液体溢出.问窄圆锥内液面上升的高度与宽圆锥内液面上升的高度之比是多少?

(A) 1:1 (B) 47:43 (C) 2:1 (D) 40:13 (E) 4:1

解设液体的体积为V,左右两边液面高度分别为h1,h2,则V=因而h1= 4h2.设放入弹子的体积为V0=左右两边液面上升高度分别为∆h1,∆h2,顶部液面的半径分别为r1,r2,则有

13.四面体ABCD中,各边长为AB= 2,AC= 3,AD=和CD=5,问它的体积是多少?

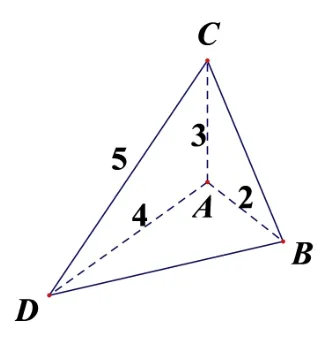
解如图所示,由于AB2+AC2=BC2,AB2+AD2=BD2,AC2+AD2=CD2,可得AB,AC,AD互相垂直,即ABCD是个直四面体.故VABCD=·AC==4,(C)正确.

14.多项式z6−10z5+Az4+Bz3+Cz2+Dz+16的根都是正整数,有可能重复.问B的取值是多少?

(A)−88 (B)−80 (C)−64 (D)−41 (E)−40

解设多项式的根为x1,x2,x3,x4,x5,x6,其中均为正整数,则z6−10z5+Az4+Bz3+Cz2+Dz+ 16 = (z − x1)(z − x2)···(z − x6),可得解得x1=x2=1,x3=x4=x5=x6= 2,于是B=−(12·2 +=−88,故(A)正确.

15.A,B,C和D的值从{1,2,3,4,5,6}中不重复地选取(即没有两个字母的取值相同),使得两条曲线y=Ax2+B和y=Cx2+D相交的不同取值方式有多少种? (不考虑曲线列出的顺序,例如,A=3,B=2,C=4,D=1 与A=4,B=1,C=3,D=2 被认为是相同的)

(A) 30 (B) 60 (C) 90 (D) 180 (E) 360

解要使得y=Ax2+B和y=Cx2+D相交,则方程Ax2+B=Cx2+D有解,即有(A −C)x2=D −B,此时A −C,D −B的符号一样.任取A,C ∈{1,2,3,4,5,6},则D,B ∈{1,2,3,4,5,6}−{A,C},大小关系须一致,则有种选择;另外不考虑曲线的顺序,故不同的取值方式共有180÷2=90 种,(C)正确.

16.在下面的数据列表中,对于1 ≤n≤200,整数n出现了n次.1,2,2,3,3,3,4,4,4,4,··· ,200,200,··· ,200.问这组数据列表中的中位数是多少?

(A) 100.5 (B) 134 (C) 142 (D) 150.5 (E) 167

解这列数共有1+2+3+···+200=×200×201=20100 个,中位数是第10050 与第10051 个数的平均值.先求得≤10050 的最大值为nmax= 141,且(nmax+1) = 10011.这说明第10050 和第10051 个数均为142,故中位数为142,(C)正确.

17.在梯形ABCD中,BC=CD= 43,并且设O是对角线的交点,P是的中点.已知OP= 11,AD的长度可以表示成其中m和n是正整数,并且n不能被任何质数的平方所整除.问m+n的值是多少?

(A) 65 (B) 132 (C) 157 (D) 194 (E) 215

解如图所示,延长CP交AB于点E,由于∆CBD是等腰三角形,P是BD中点,从而CP ⊥BD,进而CE//DA,于是AECD是个平行四边形,得EA=CD= 43.又∠CBD= ∠CDB= ∠ABD,可得∆CBP∽= ∆EBP,即得BE=BC=43,于是AB=86.

再根据∆CDO∽ ∆ABO,有即解得BP= 33,从而AD=CE= 2CP=故m+n=194,(D)正确.

18.令f是一个定义在正有理数集合上的函数,它具有性质:对于所有的正有理数a和b,f(ab) =f(a)+f(b).假设f还具有性质:对于每一个质数p,f(p) =p.问以下哪个数x满足f(x)<0?

解f(1) =f(1·1) = 2f(1)⇒f(1) = 0,f(1) ==−f(b),对于任意正有理数=f(a)−f(b),对于任意正有理数a和b;f(pn) ==nf(p),对于任意质数p,n ∈N.因此,=f(25)−f(11) =2f(5)−f(11)=2·5−11=−1<0,故(E)正确.

19.由x2+y2= 3|x −y|+3|x+y|的图像所界定的图形的面积是m+nπ,其中m和n是整数.问m+n是多少?

(A) 18 (B) 27 (C) 39 (D) 45 (E) 54

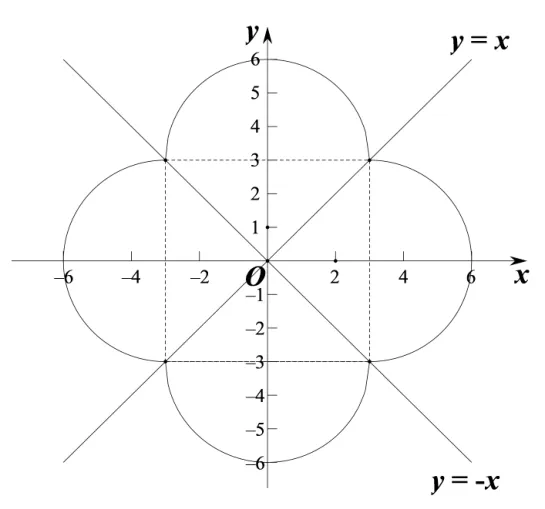
解如图所示,对点(x,y) 的位置进行讨论:(1) 在第一象限:当y≤x时,方程为x2+y2= 3(x −y)+3(x+y),化简可得(x −3)2+y2= 9,它是一个八分之一圆; 当y > x时,方程可化为x2+ (y −3)2= 9,也是一个八分之一圆; (2) 在第二象限:当y≤−x时,方程可化为x2+ (y −3)2= 9; 当y < −x时,方程可化为(x+3)2+y2=9;(3)在第三象限:当y≤x时,方程可化为(x+3)2+y2=9;当y

综上可得,该图像由四个半径为3 的半圆封闭而成,面积为62+2·π·32= 36+18π,故m+n= 36+18 = 54,(E)正确.

20.数列1,2,3,4,5 有多少种重新排列的方式,使得没有连续三项是递增的,也没有连续三项是递减的?

(A) 10 (B) 18 (C) 24 (D) 32 (E) 44

解由题意可知,符合条件的数列中,连续两项的单调性只能是:增减增减,或减增减增.用排列表示即有:13254,14253,14352,15243,15342;21435,21534,23154,24153,24351,25143,25341; 31425,31524,32415,32514,34152,34251,35142,35241.如果对集合{1,2,3,4,5}做一个置换,所得排列仍然符合条件,即以5,4 开头的排列和以1,2 开头的排列一样多.故所有符合条件的数列有(5+7)×2+8=32 个,(D)正确.

21.设ABCDEF是等角六边形,由直线AB,CD和EF所组成的三角形面积为由直线BC,DE和FA所组成的三角形的面积是六边形ABCDEF的周长可用表达,其中m,n和p是正整数,并且p不能被任何质数的平方整除.问m+n+p的值是多少?

(A) 47 (B) 52 (C) 55 (D) 58 (E) 63

解如图所示,分别向两边延长各边,交于点G,H,I,J,K,L,由题意可得,S∆GHI=由于六边形的每个内角都是120°,因此图中所有三角形的内角都是60°,即所有三角形都是等边三角形.

于是,S∆GHI=解得a+b+f=同理S∆JKL=得c+d+e=36.故六边形的周长为a+b+c+d+e+f= 36+即m+n+p= 36+16+3 = 55,(C)正确.

22.Hiram 的代数笔记有50 页,打印在25 张纸上;第一张纸包括第1 和第2 页,第二张纸包括第3 和第4 页,以此类推.有一天,他去午餐前把笔记本放在桌子上,室友决定从笔记中间借几页.当Hiram 回来时,他发现他的室友从笔记中拿走了连续的若干张纸,并且所有剩余纸张上页码的平均值正好是19.问有多少张纸被借走了?

(A) 10 (B) 13 (C) 15 (D) 17 (E) 20

解设笔记被借走了x张纸,分别是从第a张纸到第a+x −1 张纸,其中a+x −1 ≤25,页码正好是从2a −1 到2(a+x −1),页码和为(2a −1)+2a+···+2(a+x −1) =·2x= (4a+2x −3)x,而所有页码和为1 + 2 +···+ 50 = 1275,从而剩下的页码和为19(50−2x) = 1275−(4a+ 2x −3)x,整理得(4a+2x −41)x=325,解得x=13,a=10,故(B)正确.

23.青蛙Frieda 在一个3×3的方格表上开始一系列跳跃,每次跳跃都随机选择一个方向——向上、向下、向左或向右,从一个方格移动到旁边的方格.她不能斜着跳,当跳跃的方向会使得Frieda 离开方格表时,她会“绕个圈”,跳到相对的另一边.例如,如果Frieda 从中心方格开始,向上跳跃两次,第一次跳跃后她将位于最上面一行的中间方格,第二次跳跃将使得Frieda 跳到相对的边,落在最下面一行的中间方格.假设Frieda 从中心方格出发,最多随机跳跃四次,并且当到达角落方格时就停止跳跃.问她在四次跳跃中到达角落方格的概率是多少?

解记P(n) 为第n次到达角落方格的概率,显然P(1) = 0; 第一次跳跃可朝四个方向,不妨设第一次跳跃向右,则当第二次跳跃向上或向下时,可到达角落方格,概率为即P(2) =; 若第二次跳跃向左,概率为即回到出发点S,此时第四次跳跃到达角落方格的概率为; 若第二次跳跃向右,概率为此时到了S左边的方格,则第三次跳跃向上或向下可到达角落方格,即若第三次跳跃向左,概率为则回到S右边的方格,第四次跳跃向上或向下可到达角落方格,概率为从而P(4) =而其它情况均四次到达不了角落方格.故所求概率为,(D)正确.

24.设a是正实数,考虑由(x+ay)2= 4a2和(ax −y)2=a2组成的四边形的内部.对所有的a >0而言,这个区域的面积怎样用a来表示?