基于混合输入可控机构的连铸结晶器非正弦驱动装备

刘大伟，刘孟朝，任廷志，∗

（1.燕山大学机械工程学院，河北秦皇岛066004；2.燕山大学国家冷轧板带装备及工艺工程技术研究中心，河北秦皇岛066004）

基于混合输入可控机构的连铸结晶器非正弦驱动装备

刘大伟1，刘孟朝2，任廷志2，∗

（1.燕山大学机械工程学院，河北秦皇岛066004；2.燕山大学国家冷轧板带装备及工艺工程技术研究中心，河北秦皇岛066004）

以高性能伺服电机作为动力源已逐渐成为连铸结晶器非正弦驱动装备的发展趋势，针对目前电动式驱动系统的缺陷，提出两自由度混合动力驱动结晶器非正弦振动的新方案。首先以结晶器3个基本振动参数为原始变量，构建了与曲柄对称摆动运行模式相匹配的非正弦振动波形，并阐明了伺服电机和普通电机通过差动轮系运动耦合得到所需运动规律的机构原理；以保证伺服电机跟踪能力为主要目标，对NGW型差动轮系的6种运动分配模式进行结构优化，通过对比找出了最佳组合模式；最后以实现3组振动规律为例，对最佳组合模式中的电机运行方式及相应的非正弦波形进行仿真计算，以验证所提出的非正弦振动波形和振动装备的可行性，并为混合驱动系统的选型提供理论依据。

结晶器；非正弦振动；混合机构；运动分配

0 引言

结晶器非正弦振动方式被公认为是发展高效连铸和提高铸坯质量的关键，因此研发低成本、运行可靠、维护方便的先进非正弦驱动装备一直是国内外工程界的热点问题。

非正弦驱动装备根据动力源可分为液压式和电动式两大类。液压式通过液压缸直接驱动结晶器，可灵活地在线调整振动参数，但其投资成本高昂，而且液压缸存在停振、不同步等缺陷［1］。相比较而言，电动式驱动系统投资成本较低，设备维护方便，无污染。在电动缸驱动的结晶器非正弦振动系统中［2］，伺服电机频繁正反转动，运行模式不合理，影响控制精度，而且其核心传动构件滚柱丝杠的机械性能也难以与液压缸或曲柄机构相媲美；文献［3⁃4］将伺服电机的单向变速旋转经减速器和曲柄连杆机构转化成结晶器的非正弦振动，该驱动系统的波形和频率可在线可调，但却无法在线调整振幅；省掉减速机构，通过直驱电机带动曲柄连杆机构驱动结晶器，在结构上最为简单，但振幅同样无法在线调整［5］；文献［6⁃8］中采用变频电机，通过机械式非匀速机构和曲柄连杆机构合成非正弦振动，这类驱动系统无需伺服控制，降低了设备的成本，但运行中除频率外，振幅和波形均无法在线调整。

综上所述，在电动式驱动装备中，虽然曲柄连杆机构的耐磨损和抗冲击性能均优于滚珠丝杠，但以曲柄连杆机构为波形发生器的驱动装备无法实时控制振幅，不符合高效连铸的发展要求。因此提出通过混合输入可控机构驱动曲柄连杆机构实现结晶器非正弦振动，不仅可在线调整所有振动参数，而且能保证伺服电机以合理模式运行。

1 混合输入可控驱动装备的工作原理

1.1 曲柄摆动运行模式

以常见的弧型连铸机为例，曲柄连杆机构激发结晶器振动的结构简图如图1所示，结晶器振动台在板簧的约束下按弧形连铸机设计半径R做仿弧运动，其中板簧按照四连杆导向机构布置，在初始位置时板簧延长线的交点为仿弧轨迹的圆心，在结晶器小振幅振动时，可实现精确的仿弧约束。连杆AB与振动台铰接，当曲柄OA旋转时振动台产生振动。目前现场使用的结晶器驱动装备中，曲柄均为单向连续旋转，曲柄OA的长度决定了振动台的振幅。又因为运行过程中曲柄的长度不易改变，故以偏心轴为波形发生器的电动式驱动装备均无法实现振幅在线调整。

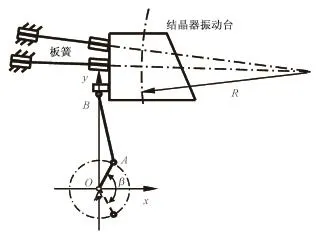
图1 结晶器波形发生机构简图Fig.1 Oscillation mechanism diagram of mold

若改变偏心轴的运转模式，使其关于x轴对称摆动运行，摆动角为β。考虑到振动台的轨迹半径和连杆AB长度均远远大于曲柄OA长度，可认为点B沿y轴往复运动，则振动台的振幅可表示为

式中，e为曲柄的长度，mm，h为结晶器振幅，mm。从式（1）中可以看出，在曲柄不变的情况下，改变摆动角β可以调整振幅h。其中结晶器的最大振幅为e，因此设计时只需保证曲柄长度e不小于结晶器的最大振幅，即可实现结晶器振幅任意调整。

为便于对结晶器振动参数的控制，以振幅h（mm），频率f（min－1）和波形偏心率α为原始变量，构建符合非正弦振动特征的曲柄速度函数。设曲柄一个回转周期中的速度函数为

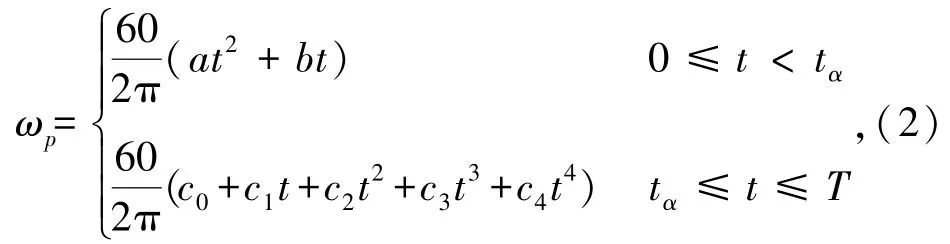
式中，ωp为曲柄角速度，rad／s，t为时间参数，s，a、 b、c0、c1、c2、c3和c4为速度函数的未知系数，在区间［0，tα）中，曲柄顺时针旋转，结晶器向下运动，在区间［tα，T］中，曲柄逆时针旋转，结晶器向上运动。其中tα与偏斜率α的关系为

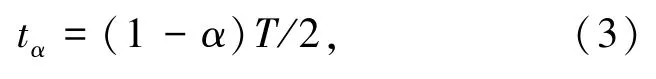
式中，T为结晶器振动周期，s，T＝60／f。

根据曲柄的运转模式可知，在区间［0，tα），ωp要满足t＝0和t＝tα时，ωp＝0，并且速度函数在区间［0，tα）上的积分值为－β，由此可得下述关于a和b的线性方程组

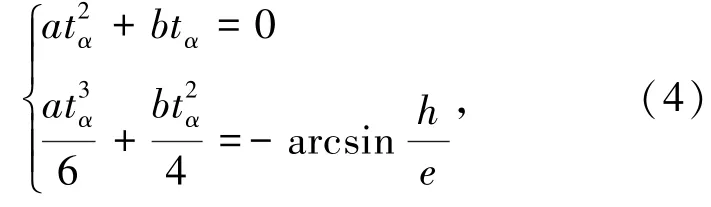
式中，tα，h和e均为已知，故可解出参数a和b。为了保证结晶器振动过程中无冲击，曲柄的角速度曲线应连续且光滑，并且曲柄正、反转的角度应相等，则在时间区间［tα，T］内，速度函数满足如下约束条件

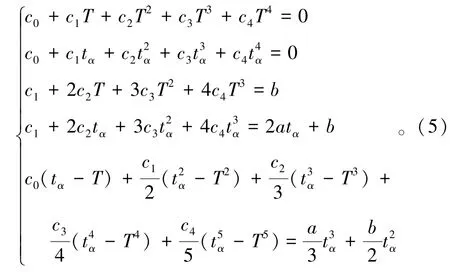
由于曲柄的角速度函数均为多项式，故式（5）中积分和求导运算非常方便，将参数a和b代入式（5），可得关于c0、c1、c2、c3和c4的线性方程组，解线性方程组（5），可求得曲柄逆时针旋转的角速度。

1.2 驱动装备的构型

文献［9］中给出通过直驱伺服电机正反转，带动曲柄实现可变摆动角和可变角速度的运行规律，但电机低频正反转不利于电机寿命，而且影响控制精度，对电机功率造成浪费。为此借鉴多自由度机构，提出恒速电机和可变速电机通过差动轮系合成出任意摆动规律的技术方案，如图2所示。

变速电机采用伺服电机，恒速电机采用三相异步交流电动机，混合驱动形式可有效地降低系统对伺服功率的需求，使设备具有低成本，大功率和柔性输出的技术优势。差动轮系为两自由度机构，伺服电机和普通电机分别与轮系中两个定轴旋转的构件固接。运行时伺服电机单向变速旋转，普通电机单向恒速旋转，通过差动轮系速度耦合特性，得到偏心轴所需的摆动规律。控制伺服电机的角速度可以对结晶器振动参数实现在线实时调整。

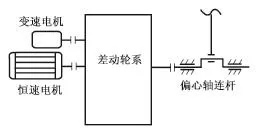
图2 混合驱动装置机构简图Fig.2 Mechanism of hybrid drive system

2 混合驱动装备的逆运动学分析及选型

在设计图2中的差动轮系时，考虑尽量减少齿轮的数量和加工难度，因此选用传动效率高，结构简单的NGW行星轮系（由内啮合齿轮副N，外啮合齿轮副W及共用的行星轮G组成）。

2.1 运动分配模式

NGW行星轮系由太阳轮1、3，行星架H和若干行星轮2组成，为便于电机安装，引入一对外啮合齿轮4和5，齿轮5可与轮系中的行星架或太阳轮固接，组成3种构型，如图3所示。

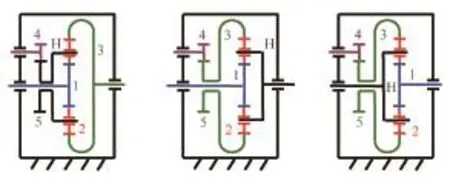
图3 驱动系统的3种构型Fig.3 Three kinds of configurations of driving system

伺服电机，普通电机和输出轴分别与太阳轮和行星架相连，能产生6种运动分配模式如表1所示。

不同运动分配模式对电机的运行特性具有决定性的影响，因此通过逆运动学分析，反求出伺服电机在6中运动模式下的速度与加速度公式，为后续选奠定基础，如表2所示。其中i13为齿轮3和齿轮1的齿数比，i45为齿轮5和齿轮4的齿数比，ωc为普通电机的额定转速，r／min，αp为输出轴的角加速度，rad／s2。

表1 运动分配模式Tab.1 Distribution model of movement

表2 伺服电机运动学参数Tab.2 Kinematic parameters of servo motor

2.2 基于伺服电机跟踪能力的选型原则

对于混合输入机构，通常期望常速电机提供主要动力，伺服电机提供辅助动力，因此功率分配的经济性是混合输入机构的首要考虑因素，如混合驱动压力机设计［10］。但本设备与其它混合驱动设备的重要区别在于对合成角速度的精度要求高，因为非正弦波形的精确程度对铸坯质量具有重要的影响，故在本设备中伺服电机的速度跟踪能力是决定设备性能的最主要因素。

为保证伺服电机的跟踪能力，应尽量减小伺服电机的速度波动范围及加速度［11］。由表2可知，在ωc和ωp一定的情况下，差动轮系的结构决定了伺服电机的运动参数，故对差动轮系提出如下设计原则：

1）保证伺服电机单向旋转，速度波动范围尽量小，并且接近额定转速，以避免出现低频共振和功率浪费；

2）使伺服电机加速度的绝对值尽量小，以保证电机跟踪能力；

3）令伺服电机额定转速不超过3 000 r／min，普通电机选取同步转速为3 000 r／min和1 500r／min的两种类型，以保证设备的通用性和经济性。

2.3 混合驱动装备的最佳构型

对于表1中的每种组合模式，在理论上都有满足上述3个原则的最优结构，为此对6种组合模式分析对比，以实现伺服电机加速度的绝对值最小为标准选取最易保证高精度运行的组合模式。

当曲柄角加速度最大时，反求出的伺服电机角加速度也最大，此时结晶器处于极限运行状态，即振幅、频率和偏斜率均为最大值。根据本文中的波形特点和现场经验，取hmax＝4.5 mm，fmax＝200 min－1，αmax＝0.25为振动参数的最大值，曲柄长度e＝6 mm＞hmax，将这些参数代入式（3）～（6）可求出差动轮系输出轴转速的最大值ωpmax＝112.5 r／min和最小值ωpmin＝－216 r／min。

另外，由于普通电机功率不同时，其额定转速略有差异，为统一计算，以电机同步转速代替额定转速，即ωc取1 500 r／min和3 000 r／min两个值。

i13和i45是决定差动轮系的结构参数，一般设计中单级圆柱齿轮的传动比不大于6，另外考虑差动轮系的尺寸，设定i13∈［1.2，7］，i45∈［1，6］。为得到表1中伺服电机角加速度绝对值最小的组合模式，采用流程图3中的计算方法，分别求取6种组合模式的最佳的结构参数i13和i45。

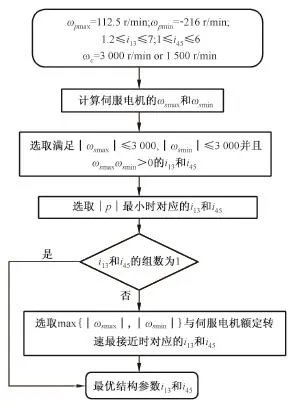
图3 差动轮系结构参数计算流程图Fig.3 Calculation flow of parameters of differential gear train

在原始参数中，普通电机的转速可选取两种，应分别进行计算，以ωc＝3 000 r／min时为例，对表1中第Ⅰ种组合模式的最优结构参数进行计算。将i13和i45作为两个变量，代入表2中第Ⅰ种组合模式的伺服电机转速公式，求出差动轮系不同结构下伺服电机的最大角速度ωsmax和最小角速度ωsmin，如图4（a）和（b）所示，其中负值表示与普通电机转速相反。

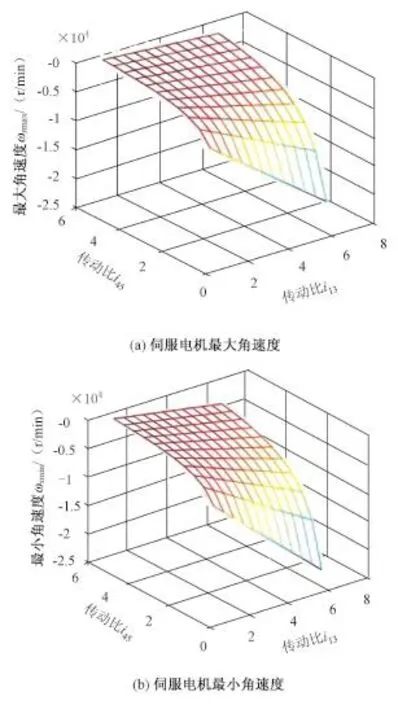
图4 不同机构参数下伺服电机角速度极值Fig.4 Extreme values of servo motor angular acceleration with different mechanism parameters

为保证伺服电机的额定转速不超过3 000 r／min，根据 3个约束条件：｜ωsmax｜≤3 000，｜ωsmin｜≤3 000和ωsmaxωsmin＞0，选取相应的i13和i45组合数据。

然后将其代入表2中第Ⅰ种组合模式的伺服电机角加速度公式，由于αp的值是在结晶器振动参数选取后就固定，因此只需比较包含i13和i45的多项式值，将该多项式定义为伺服电机角加速度系数p。对｜p｜进行比较，最小｜p｜对应的i13、i45为最佳组合。

当｜p｜为最小值时，往往对应多组i13、i45，此时需再对其进一步优化，选取｜ωsmax｜和｜ωsmin｜中最接近伺服电机额定转速时对应的i13和i45，以提高伺服电机功率利用率。经计算，6种运动分配模式的最优结构参数如表3所示。对比表3中的数据可知，第Ⅵ种组合模式下伺服电机的角加速度系数p和速度波动范围最小，而第Ⅲ模式下最大，另外第Ⅴ种与第Ⅵ种差动轮系结构相同，伺服电机运动参数也相差不多，但是当常速电机的同步转速ωc＝3 000 r／min，相应伺服电机的额定转速超过3 000 r／min，因此考虑伺服电机跟踪能力以及设备的经济性，选择ωc＝3 000 r／min时的第Ⅵ种为最佳组合模式。

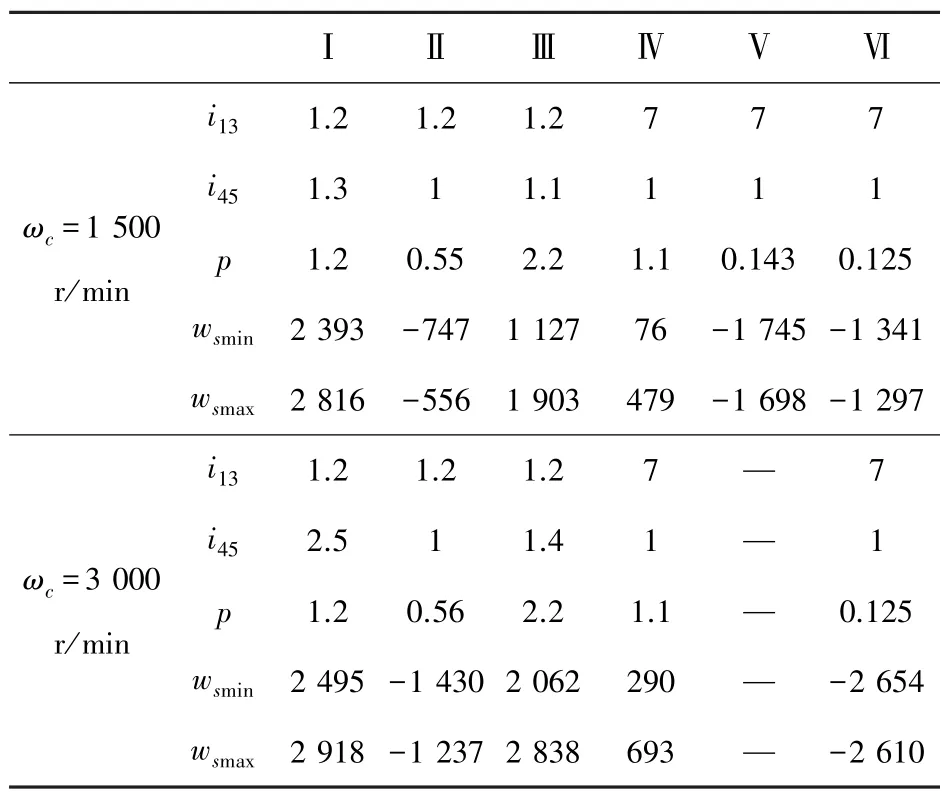
表3 6种运动分配模式下的传动比优化结果Tab.3 Optimization results of transmission ratio of six motion allocation modes

3 仿真计算

根据优化后的结构参数对第Ⅵ种组合方案进行齿数选配，令各齿轮的齿数分别为Z1＝18，Z2＝54，Z3＝126，Z4＝30，Z5＝30，行星轮个数k＝3，经验证行星轮满足均匀安装和邻接条件。另外选取普通三相异步交流电动机额定转速为 2 935 r／min，伺服电机额定转速3 000 r／min。以小方坯连铸机为例，其中小方坯的断面尺寸为250 mm× 150 mm，则结晶器随拉速不同时，分别取表4中的振动参数，结晶器振动波形和伺服电机速度曲线如图5所示，其中代号a，b，c的3条曲线分别对应表4中序号为a，b，c的数据。

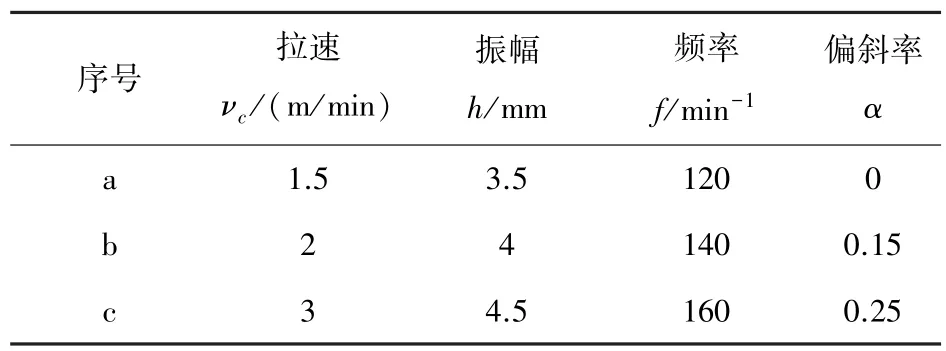
表4 结晶器基本振动参数Tab.4 Basic oscillation parameters of mould

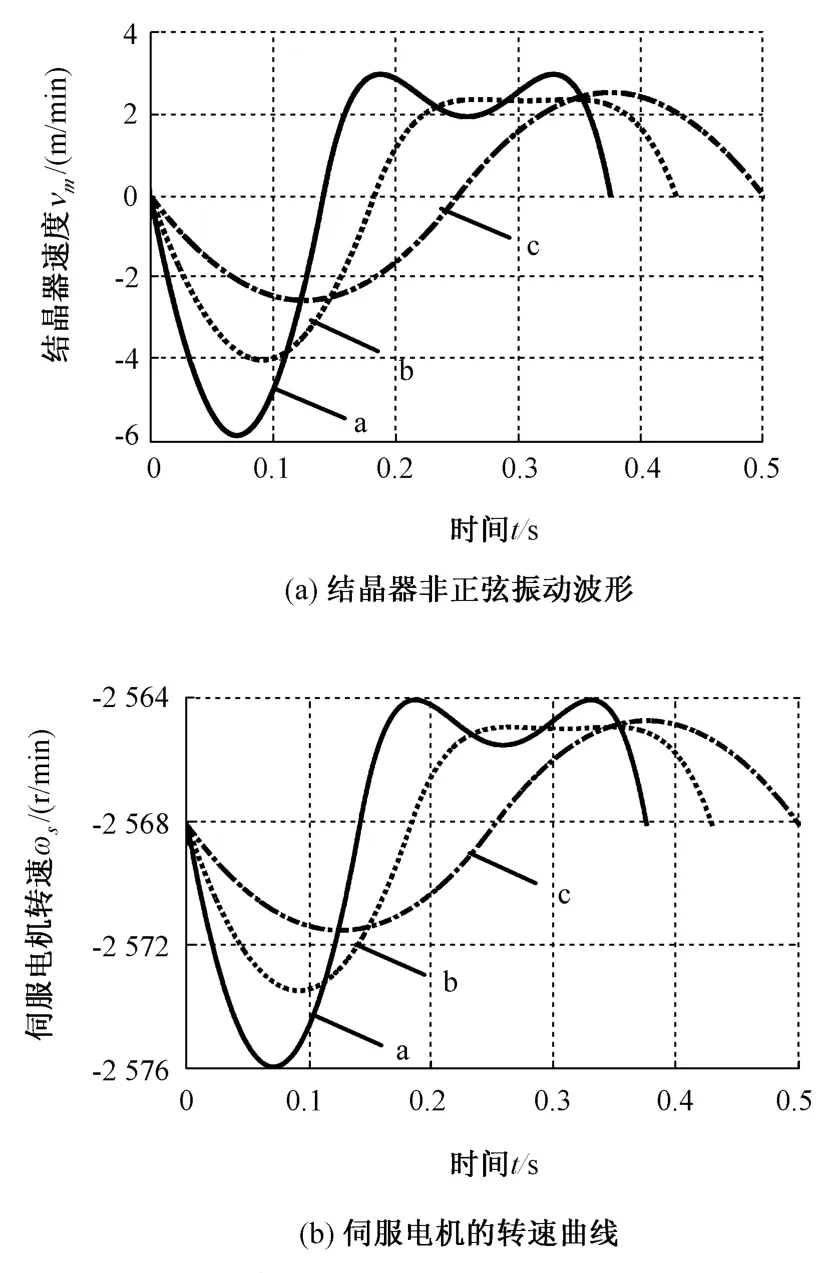
图5 不同振动参数下的非正弦波形及伺服电机转速Fig.5 Non⁃sinusoidal wave and servo motor angular velocity under different oscillation parameters

从图5（a）中可以看出，调节偏斜率α可以改变波形，随着α的减小，波形中正速度和负速度的时间比值相应减小，完全符合非正弦波形的特征。当α＝0时，正、负速度的时间相等，结晶器产生一种类似正弦波形的规律，所以本文中基于偏心轴摆动运行模式构建的结晶器波形，在生产中可以实现正弦规律与非正弦规律的切换，更加便于振动规律的控制。

从图5（b）中可以看出，在普通电机恒速输出的情况下，只需调节伺服电机的角速度，就能够实现结晶器所有振动参数的在线控制。通过合理设计差动轮系的结构和运动分配模式，不仅能保证伺服电机单向运行，而且可以使伺服电机的速度及加速度在最小范围内波动，有利于提高伺服电机的跟踪能力，确保驱动系统的精度。

4 结论

1）采用曲柄对称摆动激发结晶器非正弦振动的方式，可实现结晶器全振动参数在线实时控制。运行中伺服电机只需单向变速旋转即可实现可控摆动输出，合理的运行模式对提高伺服电机的寿命和驱动系统控制精度极为有利。

2）混合驱动装备与电液伺服驱动相比，成本低、无泄漏、维护方便；与电动缸驱动相比，避免电机频繁正反转，具有节能降耗的特点，并且其机械系统的抗冲击、耐磨损性能突出，因此具有巨大的应用潜力。

3）采用伺服电机驱动行星架，普通常速电机驱动大太阳轮，小太阳轮作为输出的运动分配方案时，伺服电机的角加速度最大值及其角速度波动范围最小，其跟踪能力最好。

［1］方涛，向忠辉，李宏磊.连铸机结晶器液压振动常见故障分析与对策［J］.机床与液压，2014，42（20）：147⁃153.

［2］訾福宁.板坯连铸结晶器电动缸非正弦振动技术与应用［J］.连铸，2013（1）：22⁃26.

［3］Yao Yunfeng，Li Xiankui，Fang Yiming，et al.Study of non⁃sinusoidal oscillation of continuous casting mold driven by servomo⁃tor［J］.Journal of Iron and Steel Research，International，2008，15（1）：558⁃562.

［4］方一鸣，李宫胤，李建雄，等.伺服电机驱动连铸结晶器振动系统建模与分析［J］.仪器仪表学报，2014，35（11）：2616⁃2623.

［5］曹铁军，王鹏，刘奎奎.直接驱动结晶器振动发生装置及其振动方法：中国，200910057435.9［P］.2009⁃06⁃17.

［6］张立平，汪建晓，卢清华，等.新型结晶器非正弦振动系统弹性振动响应的研究［J］.机械工程学报，2011，47（9）：91⁃96.

［7］刘大伟，任廷志.非圆齿轮驱动结晶器非正弦振动的研究［J］.中国机械工程，2013，24（3）：327⁃330.

［8］Zhang Xingzhong，Zheng Xueran，Liu Qingguo，et al.Investigation and application of non⁃sinusoidal oscillation technique of mold［J］. Journal of Iron and Steel，International，2013，20（2）：19⁃24.

［9］杜传得，武青，徐敦石.一种振幅在线可调的结晶器振动发生装置及其振动方法：中国，201210291325.0［P］.2012⁃08⁃16.

［10］He Yupeng，Zhao Dunsheng，Zou Jun，et al.Study of utilizing dif⁃ferential gear train to achieve hybrid mechanism of mechanical press［J］.Science in China，Series E：Technological Sciences，2007，50（1）：69⁃80.

［11］孟彩芳，张策，陆永辉，等.新型混合输入式曲柄压力机械的优化设计［J］.中国机械工程，2003，14（10）：834⁃835.

Non⁃sinusoidal driving equipment of continuous casting mold based on hybrid input mechanism

LIU Da⁃wei1，LIU Meng⁃zhao2，REN Ting⁃zhi2
（1.School of Mechanical Engineering，Yanshan University，Qinhuangdao，Hebei 066004，China；2.National Engineering Technology Research Center of Cold Rolling Strip
Equipment and Technology，Yanshan University，Qinhuangdao，Hebei 066004，China）

The application of the high performance servo motor in non⁃sinusoidal driving equipment becomes trend of the develop⁃ment of continuous casting.A new project containing two⁃DOF hybrid input machine is presented in order to overcome the defects of existing electric system.Firstly，a non⁃sinusoidal oscillation wave that matches symmetrical swing style of the crack is constructed with the three basic oscillation parameters of the mold.A differential gear mechanism driven by a servomotor and ordinary motor to implement the given angular velocity is illustrated.The structure optimization of six motion distribution modes of NGW gear train is carried out to establish the optimum mode with the goal to guarantee the traceability of the servomotor.Finally，the operation way of the servomotor and the corresponding non⁃sinusoidal waves under the optimum transmission pattern are simulated to fulfill three groups of oscillation parameters，which can validate the feasibility of the presented non⁃sinusoidal oscillation wave and equipment and provide theoretical basis for its model selection.

mold；non⁃sinusoidal vibration；hybrid mechanism；motion distribution

TH132

A

10．3969／j．issn．1007⁃791X．2015．05．005

1007⁃791X（2015）05⁃0414⁃06

2015⁃08⁃19 基金项目：河北省自然科学基金钢铁联合研究基金资助项目（E2011203078）；燕山大学博士基金（B870）

刘大伟（1984⁃），男，河北沧州人，博士，讲师，主要研究方向为高效连铸装备及工艺；∗通信作者：任廷志（1960⁃），男，黑龙江大庆人，博士，教授，博士生导师，主要研究方向为机械设计及智能化，Email：rtz＠ysu.edu.cn。