基于优化支持向量机的热耗率预测方法

刘 超，牛培峰，∗，段小龙，李国强，张维平，陈 科

（1.燕山大学电气工程学院，河北秦皇岛066004；2.秦皇岛职业技术学院机电工程系，河北秦皇岛066100）

基于优化支持向量机的热耗率预测方法

刘 超1，牛培峰1，∗，段小龙1，李国强1，张维平2，陈 科1

（1.燕山大学电气工程学院，河北秦皇岛066004；2.秦皇岛职业技术学院机电工程系，河北秦皇岛066100）

针对传统的汽轮机热耗率计算模型精度较低的问题，构建了一种基于改进生物地理学优化算法优化支持向量机的热耗率预报模型。首先，提出改进的生物地理学优化算法以加强算法的优化能力，并通过4个典型的测试函数验证算法的有效性。其次，采用支持向量机建立汽轮机热耗率的预报模型，并选用径向基函数作为核函数，用改进的生物地理学优化算法优化该模型参数。最后，结合某火电站600 MW超临界汽轮机组现场数据进行热耗率预报的仿真研究，结果表明基于该算法建立的汽轮机热耗率预报模型具有较高的预报精度。

热耗率；汽轮机；生物地理学优化算法；支持向量机

0 引言

汽轮机热耗率是反映机组热经济性的重要指标，精确的热耗率值是机组安全运行和优化控制等问题的关键，同时对于获取汽轮机最优初压也有着重要意义，因此，建立热耗率预测模型是十分必要的。超临界汽轮机系统中存在众多的影响热耗率因素，受到诸如主蒸汽温度、流量、压力，再热蒸汽的温度、流量、压力，发电输出功率，汽轮机自身健康情况等多种因素影响［1］。传统的热耗率计算主要是通过热力学分析［2］，运用热力学计算公式得到的。但常规计算受到计算方法的限制，需要做出一些假设和简化，但是机组在实际运行中受到负荷频繁变动、煤质变化、环境温度改变等因素的影响，往往偏离设计工况，这种情况下热力学计算公式很难达到满意的效果。同时，对于参数之间具有强耦合、非线性等特征的物理过程，难以用机理模型来描述。

目前，一种可行办法是利用回归方法计算热耗率值。文献［3］采用偏最小二乘算法预测热耗率值，文献［4］采用BP神经网络分析汽轮机的运行特性。但由于神经网络模型易发生过拟合，从而降低网络的泛化能力。近年来，为了克服神经网络固有的缺点，基于统计学习理论的支持向量机（support vector machine，SVM）被提出并得到广泛的应用［5⁃7］，这些研究表明SVM具有较好的模拟能力。因此，本文采用SVM建立汽轮机热耗率的预报模型，并选用径向基函数作为核函数。SVM建模过程中参数的选择对模型精度和泛化能力有很大的影响，其最优参数的选择问题其实就是一个组合优化问题，存在大量的智能优化算法用来解决支持向量机的参数选择问题。

生物地理学优化（biogeography⁃based optimiza⁃tion，BBO）算法是由美国学者Simon D根据生物地理学原理于2008年提出的一种群智能的随机优化算法［8］。BBO算法具有易于理解、操作简单、易于实现的优点，该算法已经被证明是一种较好的全局优化方法。但基本的生物地理学优化算法又易于陷入局部最优，导致搜索成功率不高［9］。本文在混合迁移算子的基础上引入了模拟退火思想［10］，提出了基于模拟退火的混合生物地理学优化算法（blended biogeography⁃based optimization based on simulated annealing，B⁃BBO⁃SA），混合迁移算子保证迁移过程中种群的多样性，引入具有强大局部搜索能力的模拟退火算法以避免算法陷入局部最优解的不足，同时，仿真实验验证了改进算法的有效性。

本文结合超临界汽轮机的工艺特点，构造了一种基于SVM建立热耗率预报模型，并采用B⁃BBO⁃SA算法解决SVM参数优化的问题。实验结果表明该预报模型具有良好的预报精确和泛化能力，大大提高了汽轮机热耗率预报的准确度。

1 基于模拟退火的混合生物地理学优化算法（B⁃BBO⁃SA）

1.1 生物地理学优化算法

生物地理学优化（BBO）算法是基于生物地理学中生物种群在栖息地间的分布、迁移和灭绝规律而提出的，它主要是模拟生物种群在栖息地间的迁移操作和突变操作来解决各种工程优化问题。各栖息地生物种群间以迁入概率（Immigration rate，λ）和迁出概率（Emigration rate，μ）来决定信息交换和信息共享，以变异概率（Mutation rate，Mu）来增加物种的多样性。借助精英策略来保护每代中最优的个体，在此通过设定它们的迁入率λ＝0，使其在进化中不被破坏，从而把它们优良的特征保存到下一代，这样可以保证种群在进化过程中不会退化。迁入率λ（s）和迁出率μ（s）可以描述成适应度指数（s）的函数，单个栖息地生物种群线性迁移模型如图1所示。

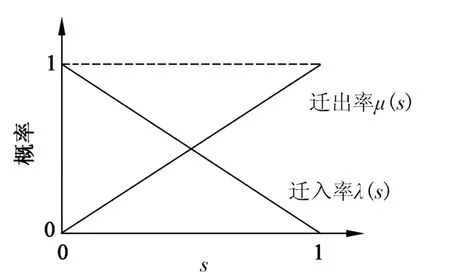
图1 单个栖息地生物种群线性迁移模型Fig.1 Single habitats population migration of linear model

迁入率λ和迁出率μ可以由式（1）计算得到：

其中，s∈［0，1］表示个体的适应度值。

BBO中用迁入率λi来选择迁入个体Hi，用迁出率μj来选择待迁出个体Hj，迁移操作可以表示为

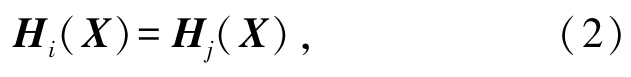
其中，Hi（i＝1，2，…，n）代表待寻优个体的一个候选解，X表示个体的一个特征向量。迁移操作完成后，通过突变概率Mu对生物种群进行随机突变性操作来增加物种的多样性。

1.2 模拟退火算法

模拟退火（simulated annealing，SA）算法［10］是由Kirkpatrick S在1983年提出的。SA算法受启发于金属固体从高温到低温的物理降温过程，当金属物体离开加热源后会经过一个降温过程，只要温度降低的足够慢，它会在每个温度下达到一个热平衡，最后会趋于周围的环境温度从而达到平衡状态。SA算法在迭代过程中既接受使目标值变好的个体，又以一定的概率接受使目标值变差的个体，从而提高算法在迭代过程跳出局部最优解的可能性，使算法能够更好地趋于全局最优解。其具体步骤如下：

1）初始化温度Tk（k＝0），在可行域随机产生初始解x0，并计算目标函数值f（x0）；

2）在温度Tk下重复执行如下操作，直到达到Tk温度下的终止条件：

a）在解x的基础上产生新的可行解x′，并计算目标函数值f（x′）；

b）求出Δ＝f（x′）－f（x），如果Δ≤0，接受x′，并令x＝x′；如果Δ＞0，以概率exp（－Δ／Tk）＞rand接受x′，否则x值不变；

3）降温操作Tk＝CTk－1，C为降温系数。达到进化结束的条件，结束退火过程；否则转向步骤（2）。

1.3 B⁃BBO⁃SA算法

鉴于基本生物地理学优化算法在迭代过程中易于陷入局部最优、早熟收敛的不足，本节在混合迁移算子的基础上引入模拟退火算法，提出一种基于模拟退火的混合生物地理学优化算法（blended biogeography⁃based optimization based on simulated annealing，B⁃BBO⁃SA）以提高了算法的优化能力。在迁移操作中，采用式（3）的混合迁移（blended migration）算子：

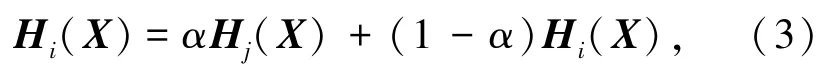
式中，α为0到1间的常数。从式（3）中可以看出，混合迁移操作后的新个体既保留了迁入个体自身的一些特征又可以得到迁出个体的一些特征，从而组成迁入个体中新的特征变量。

为避免算法陷入局部最优解，在BBO算法中引入模拟退火算法。为了提高算法的效率，只对迁移操作后的最好个体按照式（4）进行退火操作：

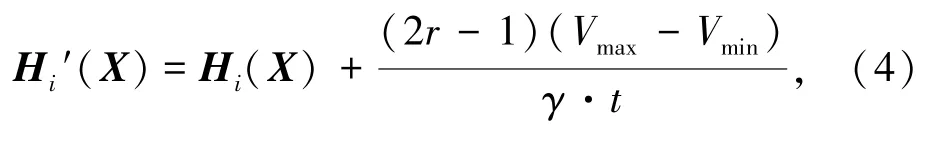
式中，r为0到1之间的随机数，Vmax、Vmin分别为可行域的上、下限，γ为步长的控制参数，t表示进化的代数。在进化前期，t较小，算法可以进行广域的搜索，有助于跳出局部最优解；在进化后期，个体靠近最优解，这时搜索范围随着t值逐渐变大而渐小，局部搜索的作用越来越强，在最优解的小邻域内进行搜索，增大了找到最优解的可能性。用式（5）判断新个体变量的合法性：

本文的B⁃BBO⁃SA算法具体实现步骤如下：1）参数的设定和种群的初始化；

2）计算每个个体的适应度值s，并计算迁入率λi和迁出率μi，同时保存精英个体；

3）用λi选择需要进行迁入的个体Hi，用μj选择需要迁出的个体 Hj，根据式（3）进行迁移操作；

4）选出迁移操作后的最优个体 Hi按照式（4）进行模拟退火操作；

5）根据突变概率Mu进行突变操作；

6）降温操作Tk＝CTk－1。达到进化代数，结束进化操作，否则，转向步骤（2）。

1.4 B⁃BBO⁃SA算法验证

本节通过两个性能指标：平均最优解（Mean）和标准差（Std）来定性验证B⁃BBO⁃SA算法的优化性能。采用4个基准测试函数［11］：F1（Schwefe12）、F2（Step）、F3（Penalty2）、F4（Ackley）。其中F1和F2为单峰函数；F3和F4为多峰函数，它们有多个极值点。在此并分别与BBO、正弦迁移模型［9］（BBO⁃C）、混合迁移算子和高斯突变策略［12］（B⁃BBO⁃G）进行比较。

测试中所有算法具有相同的参数设置：初始种群规模为100，个体维数为30，最大进化代数为200，突变概率 Mu＝0.005，混合迁移操作中 α＝0.9，精英个体数为1，控制步长γ＝3，初始温度T0＝1 000℃，降温系数C＝0.8。各种算法在每次迭代独立运行30次，各算法的测试结果见表1。

表1 基准测试函数的仿真结果Tab.1 Simulation results of benchmark test functions

从表1中可以看出，在单峰函数F1上B⁃BBO⁃SA有较好的寻优能力，F2上 B⁃BBO⁃SA与 B⁃BBO⁃G的平均最优解大体相同，整体上B⁃BBO⁃SA优化能力要高于BBO和BBO⁃C算法。在高维多模函数F3、F4上，B⁃BBO⁃SA表现出很好的优化能力。特别是在F3上，相对于BBO优化的最优值4.802 6，B⁃BBO⁃SA为2.988 7e⁃5要远远好于BBO算法。

下面以F1～F4为例，具体研究B⁃BBO⁃SA算法的寻优过程。由独立运行20次后的平均目标适应度值绘制进化曲线，进化曲线如图2～5。从图2～5比较结果可以看出，B⁃BBO⁃SA算法对于目标函数的优化性能和收敛速度相对其它3种算法来说都有明显的提升。在进化前期由于混合迁移算子的加入保证进化过程中种群的多样性，增大算法跳出局部最优解的可能性；进化后期模拟退火策略增强了算法的局部搜索能力，提高了解的精度，从而验证了B⁃BBO⁃SA算法的有效性。

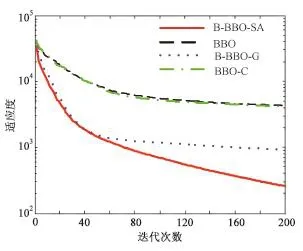
图2 F1进化曲线Fig.2 Fitness performance curve of function F1

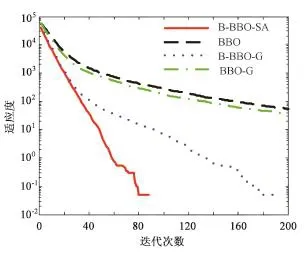
图3 F2进化曲线Fig.3 Fitness performance curve of function F2

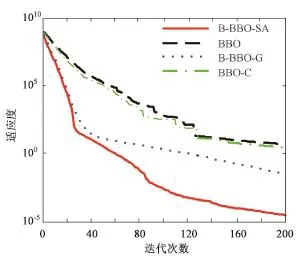
图4 F3进化曲线Fig.4 Fitness performance curve of function F3

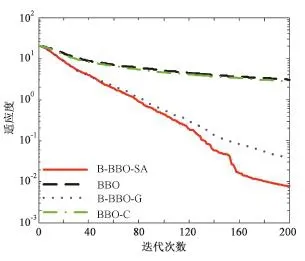
图5 F4进化曲线Fig.5 Fitness performance curve of function F4

2 支持向量机原理

支持向量机方法是建立在统计学习理论的VC维理论和结构风险最小原理基础上，能较好地解决小样本、非线性、高维数和局部极小点等实际问题，具有很强的泛化能力。基本思路是通过一个非线性变换ϕ（x）把一组训练样本（xi，yi）映射到高维特征空间H中。SVM用下式函数对未知函数进行估计［5⁃7］：

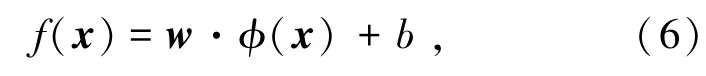
其中，w为权值向量，b为通过风险函数最小化得出的阈值。

假设所有训练样本可以在精度ε下无误差的进行函数拟合，考虑到允许拟合误差的存在，引入松弛变量ξi≥0和，则问题转化为如下最小化函数：

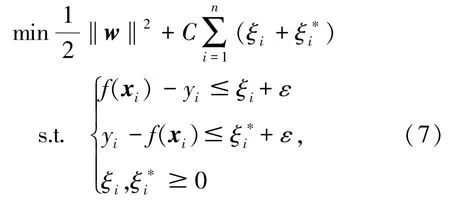
通过引入拉格朗日函数将式（7）转化为对偶问题，解对偶问题得到训练集的测量模型

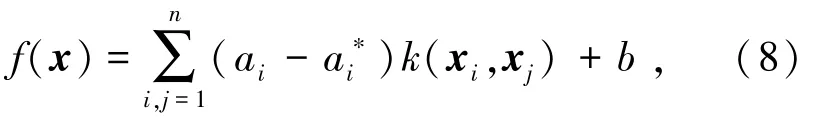
其中，ai，为拉格朗日乘子，其中只有少部分ai，不为0，k（xi，xj）为核函数。

3 B⁃BBO⁃SA优化SVM的热耗率预报模型

3.1 SVM参数选择

本文采用支持向量机作为汽轮机热耗率的预报模型，SVM是将热耗率相关的非线性样本数据映射为高维控制的线性输出，如式（8）。文中采用径向基函数（radial basis function，RBF）作为核函数

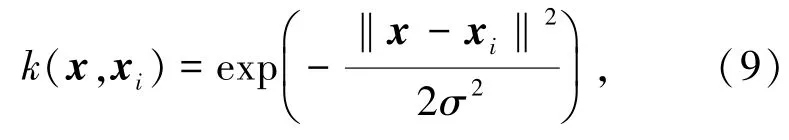
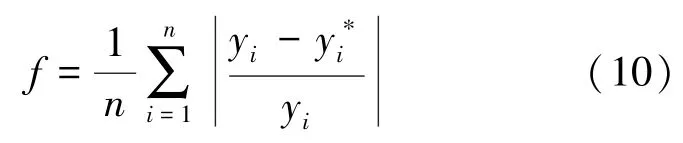
其中，f为适应度函数，yi为实际值，为预报值，n为训练样本个数。

3.2 热耗率预报模型仿真分析

汽轮机的热耗率是指汽轮发电机组每发出1 kW·h的电所消耗的热量，其大小体现了汽轮机机组能量转换过程中的一项重要经济指标。针对传统的汽轮机热耗率计算模型精度较低的问题，本文构建了一种基于改进生物地理学优化算法优化支持向量机的热耗率软测量预报模型。根据文献［1］、［5］最终选定发电负荷、主蒸汽温度、主蒸汽压力、再热器出口蒸汽温度、再热器出口蒸汽压力再热减温水流量、过热减温水流量等20个参数作为SVM模型的输入参数，热耗率作为SVM模型的学习目标。影响汽轮机热耗率计算有两大因素：①汽轮机性能及“健康状况”；②机组的运行参数。

汽轮机运行过程往往具有周期性重复运行的特点，运行参数中充分包含了在不同工况范围内的动态特性信息，也蕴含有汽轮机“健康状况”的信息。机组运行参数中的主汽流量的测量对热耗率计算的精度影响较大，因此，主汽流量的准确计量非常重要。常规的标准节流孔板测量具有压缩性的过热蒸汽，其精度较低。本文数据来源的火电厂，其主汽流量的计量是通过在锅炉的给水管道上安装节流孔板，通过测量给水流量，然后间接换算成主蒸汽流量，其计量结果有较高的精度。最后，通过热力分析，在线计算获得模型可靠的学习目标——热耗率。本文通过大量的运行参数，采用优化的SVM来建立汽轮机热耗率的软测量模型。以某火电厂 600 MW超临界汽轮机组（CLN600⁃24.2／556／556⁃I型）为研究对象，其中289数据样本是由集散控制系统中每隔1小时采样一次而得，每天采集24组，基本覆盖了汽轮机组全天运行的典型工况［1］。将其中265组数据用来训练模型，余下的24组数据作为测试数据。

根据3.1节优化SVM预报模型的参数，选取参数范围：0.000 1≤ε≤0.1，0.1≤σ2≤1 000，1≤C≤10 000。设置B⁃BBO⁃SA种群规模为30，最大进化代数为100。SVM参数经过B⁃BBO⁃SA优化得到最优组合：ε＝0.001 7，σ2＝0.772 4，C＝7.140 2×103。为进一步验证B⁃BBO⁃SA⁃SVM模型预报能力，将其与1.4节中表现良好的B⁃BBO⁃G算法优化SVM预报模型进行比较。SVM参数经过B⁃BBO⁃G优化得到最优组合：ε＝0.046 5，σ2＝9.919 2，C＝6.727 9×103。在对训练集训练以及对测试集的预报中，B⁃BBO⁃SA⁃SVM模型的平均绝对误差值分别为0.183 9和51.468 3，而B⁃BBO⁃G⁃SVM模型的平均绝对误差值分别为56.017 7和98.744 1。数据显示B⁃BBO⁃SA⁃SVM热耗率预报模型有很小的训练误差，同时，针对测试样本，B⁃BBO⁃SA⁃SVM模型有更好泛化能力。最后将 B⁃BBO⁃SA⁃SVM与标准SVM热耗率预报模型进行对比，针对训练集和测试集，其热耗率预测模型的平均绝对误差分别为78.941 5、145.025 9，其预测结果明显大于B⁃BBO⁃SA⁃SVM优化的结果，进而验证了B⁃BBO⁃SA算法的有效性。

为进一步验证模型的泛化能力，图6为 B⁃BBO⁃SA⁃SVM、B⁃BBO⁃G⁃SVM和SVM模型对24组测试样本的热耗率预测结果，图7为预测误差。从图6中可以看出，SVM模型不能较好地预报出热耗率，B⁃BBO⁃SA⁃SVM热耗率预测效果要明显好于SVM预测效果；针对其中9个样本（2，4，5，6，9，11，12，18，21）B⁃BBO⁃G⁃SVM的热耗率预测结果与B⁃BBO⁃SA⁃SVM的预测结果有比较接近的预测效果，剩余15测试样本，B⁃BBO⁃SA⁃SVM均有较好的预测效果。图7显示了预测值与真实值之间的绝对误差，圆点实线为B⁃BBO⁃SA⁃SVM预测误差，其绝对误差值大部分都在［－85，95］kJ·（kW·h）－1范围内；图7中三角形虚线的曲线为SVM的预测绝对误差，其绝对误差值大部分都超B⁃BBO⁃SA⁃SVM的绝对误差值，最大值已达到450 kJ·（kW·h）－1。因而B⁃BBO⁃SA⁃SVM模型显示了更出色的泛化能力。

图6 热耗率预报曲线Fig.6 Heat rate prediction curve

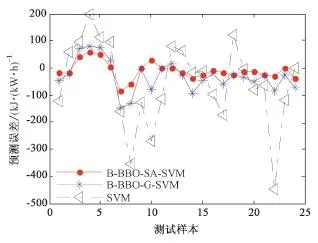
图7 各模型预报误差曲线Fig.7 Prediction error curve of each model

4 结束语

问题，本文提出了一种基于改进的生物地理学优化算法（B⁃BBO⁃SA）优化支持向量机（SVM）模型参数的方法，用于建立汽轮机热耗率的预报模型。改进的生物地理学优化算法引入了混合迁移算子和模拟退火算法，混合迁移操作能够使迁入个体和迁出个体的对应变量进行有效的组合，在进化过程中能够保持种群的多样性，增强全局寻优能力，模拟退火算法可以增强算法的局部搜索能力，提高了跳出局部最优解的可能性，从而增强算法的优化能力。最后将所建立的B⁃BBO⁃SA⁃SVM热耗率预报模型应用在某600 MW超临界汽轮机组的热耗率预报中，结果验证了该模型具有较高的预报精度和良好的泛化能力。

［1］刘超，牛培峰，游霞.反向建模方法在汽轮机热耗率建模中的应用［J］.动力工程学报，2014，239（11）：867⁃872.

［2］郭江龙，常澍平，姚力强，等.大型汽轮机复合滑压运行参数寻优方法研究［J］.汽轮机技术，2010，52（6）：467⁃469.

［3］张文琴，付忠广，靳涛，等.基于偏最小二乘算法的热耗率回归分析［J］.现代电力，2009，26（5）：56⁃59.

［4］李勇，王海荣.基于BP网络的汽轮机运行特性方程［J］.热能动力工程，2002，17（3）：268⁃270.

［5］王雷，张欣刚，王洪跃，等.基于支持向量回归算法的汽轮机热耗率模型［J］.动力工程，2007，27（1）：19⁃23.

［6］王春林，周昊，李国能，等.基于支持向量机与遗传算法的灰熔点预测［J］.中国电机工程学报.2007，27（8）：11⁃16.

［7］Niu Peifeng，Liu Chao，Li Pengfei.Optimized support vector regres⁃sion model by improved gravitational search algorithm for flatness pattern recognition［J］.Neural Computing and Applications，2015，26（5）：1167⁃1177.

［8］Simon D.Biogeography⁃based optimization［J］.IEEE Transactions Evolutionary Computation.2008，12（6）：702⁃713.

［9］Ma H P，Simon D.Analysis of migration models of biogeography⁃based optimization using Markov theory ［J］.Engineering Application of Artificial Intelligence，2011，24（6）：1052⁃1060.

［10］戚孝铭，施亮.基于模拟退火及蜂群算法的优化特征选择算法［J］.计算机工程与设计，2013，34（8）：2917⁃2921.

［11］P Venkata Rao，Vivek Patel.An improved teaching⁃learning⁃based optimization algorithm for solving unconstrained optimization problems［J］.Scientia Iranica D，2013，20（3）：710⁃720.

［12］Gong W Y，Cai Z H，Ling Charles X，et al.A real⁃coded biogeogra⁃phy⁃based optimization with mutation［J］.Applied Mathematics and Computation，2010，216（9）：2749⁃2758.

针对汽轮机热耗率传统模型难以精确求解的

Heat rate forecasting based on optimized support vector machines

LIU Chao1，NIU Pei⁃feng1，DUAN Xiao⁃long1，LI Guo⁃qiang1，ZHANG Wei⁃ping2，CHEN Ke1
（1.School of Electrical Engineering，Yanshan University，Qinhuangdao，Hebei 066004，China；2.Department of Electromechanical Engineering，Qinhuangdao Institute of Technology，Qinhuangdao，Hebei 066100，China）

To deal with the low precision of the traditional calculation model，a new optimized support vector machine（SVM）based on improved biogeography⁃based optimization（BBO）algorithm is introduced to prediction steam turbine heat rate.First，an improved BBO algorithm called B⁃BBO⁃SA is proposed to enhance the performance of original BBO algorithm by introducing a hy⁃brid migration operator and simulated annealing.At the same time，the validity of B⁃BBO⁃SA is evaluated by four classical test functions.Then，SVM is employed to establish the prediction model of steam turbine heat rate，and the radial basis function is se⁃lected as the kernel function，in which，the B⁃BBO⁃SA is employed to serve as a method for pre⁃selecting SVM parameters in order to build heat rate prediction model and obtain a well⁃generalized model.Finally，a hybrid B⁃BBO⁃SA⁃SVM model is established for heat rate forecasting of a 600 MW supercritical steam turbine unit.Experimental results show that the optimized SVM model by B⁃BBO⁃SA has well regression precision and generalization ability.

hate rate；steam turbine；biogeography⁃based optimization algorithm；support vector machine

TK26

A

10．3969／j．issn．1007⁃791X．2015．05．007

1007⁃791X（2015）05⁃0425⁃06

2015⁃06⁃20 基金项目：国家自然科学基金资助项目（61403331，61573306）；河北省自然科学基金资助项目（F2010001318）

刘超（1986⁃），男，四川巴中人，博士研究生，主要研究方向为人工智能技术与复杂工业系统的优化控制；∗通信作者：牛培峰（1963⁃），男，吉林舒兰人，博士，教授，博士生导师，主要研究方向为复杂工业系统的智能建模与智能控制，Email：npf882000＠163.com。