n（3⁃RPS）混联机构静力学和刚度模型

胡 波，宋春晓，王安东，崔 鹤，李 博，于晶晶

（1.燕山大学河北省并联机器人与机电系统实验室，河北秦皇岛066004；2.先进锻压成形技术与科学教育部重点实验室（燕山大学），河北秦皇岛066004）

n（3⁃RPS）混联机构静力学和刚度模型

胡 波1，2，∗，宋春晓1，2，王安东1，2，崔 鹤1，2，李 博1，2，于晶晶1，2

（1.燕山大学河北省并联机器人与机电系统实验室，河北秦皇岛066004；2.先进锻压成形技术与科学教育部重点实验室（燕山大学），河北秦皇岛066004）

建立了一种混联机构n（3⁃RPS）的静力学和刚度模型。首先，基于这类机构运动特性分析了n（3⁃RPS）机构的速度传递关系。其次，基于虚功原理建立了n（3⁃RPS）机构的静力学模型。最后，建立了n（3⁃RPS）机构的刚度模型，求取了n（3⁃RPS）机构的变形。为验证机构刚度和变形模型的正确性，建立了2（3⁃RPS）机构和3（3⁃RPS）机构的有限元分析模型并进行仿真，研究结果表明计算结果和有限元仿真结果基本一致。本文中建立n（3⁃RPS）机构刚度的方法也适合其它混联机构。

混联机构；静力学；刚度；变形

0 引言

近几十年来，并联机构引起了国内外学者的广泛研究，新机构不断涌现［1⁃3］，并联机构的一些基本理论体系已经初步建立。然而，和并联机构相比，混联机构的研究却相对较少，这里所指的混联机构是由两个或多个并联机构串联而成的机构。这类机构兼具串联和并联机构的共同优点，相对并联机构具有较大的工作空间和活动能力，相对串联机构具有较强的刚度，可用作锻造机混联操作手、仿生机器人、微纳加工机器人等机械本体［1］。在该领域，HU和LU［4］研究了由一个3⁃RPS机构和一个3⁃SPR机构构成的混联机构的运动学问题。JAIME［5］研究了2（3⁃RPS）混联机构的自由度问题。Zeng［6］对这类机构开展了型综合研究。在并联机构的刚度研究方面，国内外学者也做了很多工作，GOSSELIN［7］建立了只考虑驱动因素的刚度模型，TSAI［8］分析和比较了Tricept机构和3⁃UPU机构的刚度模型。Klimchika［9］研究了内力和外力共同作用下的并联机构刚度模型，ZHANG［10］采用建立的运动静力学模型分析机构刚度。李剑锋等［11］对具有大位置空间的2PUS⁃PU并联机构刚度进行了分析。对于由并联机构串联而成的混联机构的研究一直很缓慢，且针对这类机构研究也多停留在由两个并联机构串联而成的机型上［4⁃6］。对于由任意个并联机构串联而成的机构，理论研究相对滞后。基于此，本文致力于建立由n个少自由度3⁃RPS并联机构串联得到的混联机构n（3⁃RPS）的静力学和刚度模型。针对该机构建立的理论模型同样适合于其他混联机构。

1 n（3⁃RPS）机构介绍

本文所研究的n（3⁃RPS）机构是由n个具有相同构型的3⁃RPS机构串联而成的机构。第i（i＝2，…，n）个3⁃RPS机构的下平台和第 i－1个3⁃RPS机构的上平台共面，尺寸相同，并且中心重合。第i个3⁃RPS机构的下平台相对于第i－1个3⁃RPS机构的上平台逆时针旋转（－1）i60°。图1为一个由3个3⁃RPS机构组成的3（3⁃RPS）混联机构的机构简图。

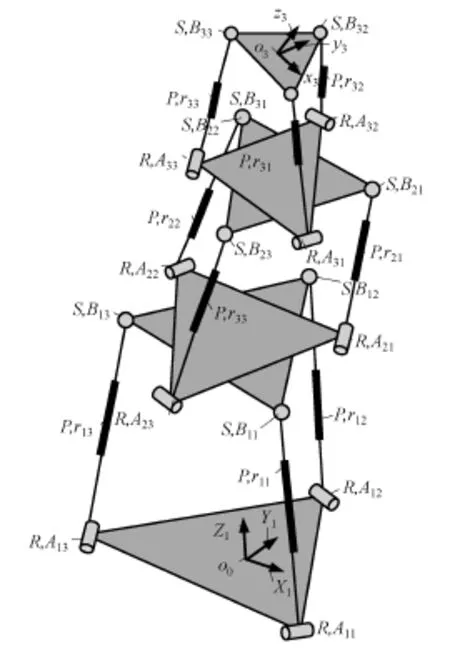
图1 3（3⁃RPS）机构简图Fig.1 Sketch of 3（3⁃RPS）manipulator

n（3⁃RPS）机构的第i个3⁃RPS机构有1个下平台ni0，1个上平台ni1和3个RPS分支rij（i＝1，2，…，n；j＝1，2，3）。ni0和ni1都是等边三角形，其中下平台ni0中心到其各端点的距离为Li，上平台ni1中心到其各端点的距离为li。rij通过球副S连接上平台ni1于Bij点，通过转动副R与下平台连接于Aij，rij垂直于其对应的R副。沿着rij有1个移动副P。则ni0可视为基座，ni1可视为该混联机构的末端平台。

规定第i（i＝1，2，…，n）个3⁃RPS机构的上平台中心为oi，则其下平台中心为oi－1，第1个3⁃RPS机构的下平台中心为o0。规定｛ni0｝为以各机构下平台中心oi－1（i＝1，2，…，n）为原点建立的坐标系oi－1⁃XiYiZi，｛ni1｝为以各机构上平台中心oi为原点建立的坐标系oi－xiyizi（i＝1，2，…，n）。坐标轴满足（Xi∥Ai1Ai3，Yi⊥Ai1Ai3，Zi⊥Xi，Zi⊥Yi，xi∥Bi1Bi3，yi⊥Bi1Bi3，zi⊥xi，zi⊥yi）。

2 n（3⁃RPS）机构的速度传递关系

n（3⁃RPS）机构第i个3⁃RPS机构下平台各端点Aij（i＝1，2，…，n；j＝1，2，3）在坐标系｛ni0｝中的坐标为

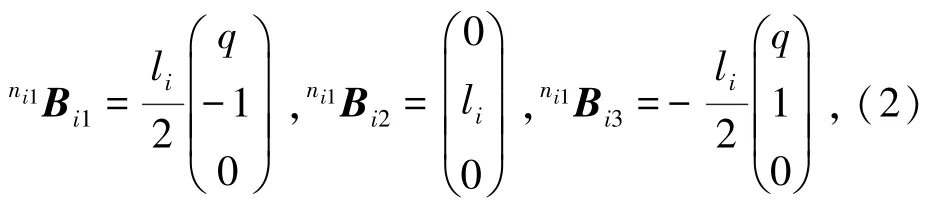
端点Bij在｛ni0｝中的坐标表达如下

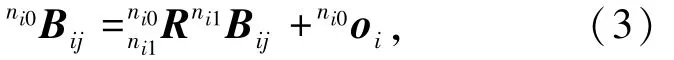
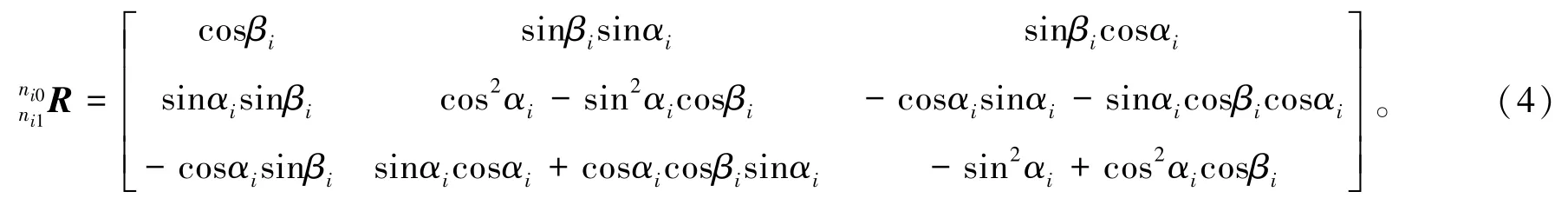
由文献［12］知，对于单个的3⁃RPS机构，当分别给定第i个3⁃RPS机构上平台相对于下平台的独立位姿参数为αi、βi、Zoi时（其中αi、βi为上平台相于下平台旋转的欧拉角，在文献［12］中用来表达上平台相对于下平台的姿态，Zoi为上平台中心相对于下平台的坐标），上机构和下机构的杆长rij可由下式求出：

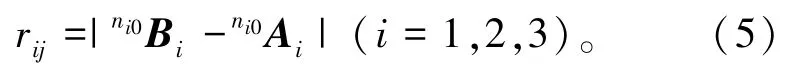
由于第i个3⁃RPS机构的下平台相对于第i－1个3⁃RPS机构的上平台逆时针旋转了60°，可得坐标系｛ni0｝相对于｛n（i－1）1｝的旋转矩阵为

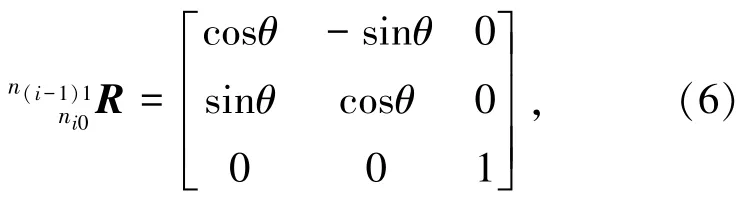
其中，θ＝60°×（－1）i－1，i＞1。

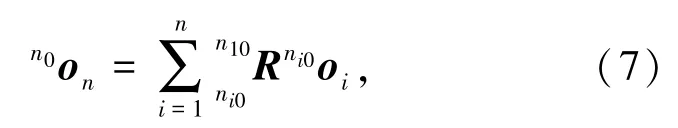
末端平台相对于基座的旋转矩阵可表达为

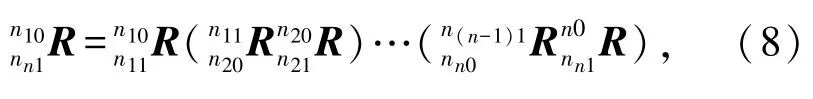
末端平台相对于静平台的角速度可表达为

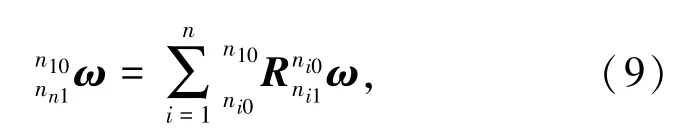
设有任意两矢量m＝［mxmymz］T，n＝［nxnynz］T，

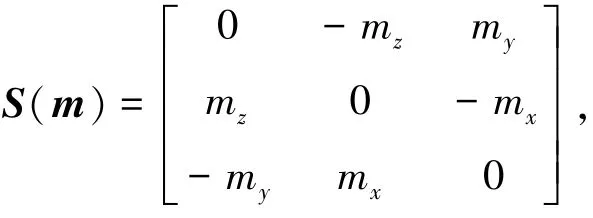
则两矢量及S（m）满足

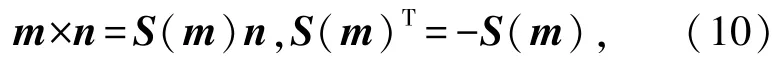
对式（7）求导，并结合（10）可得

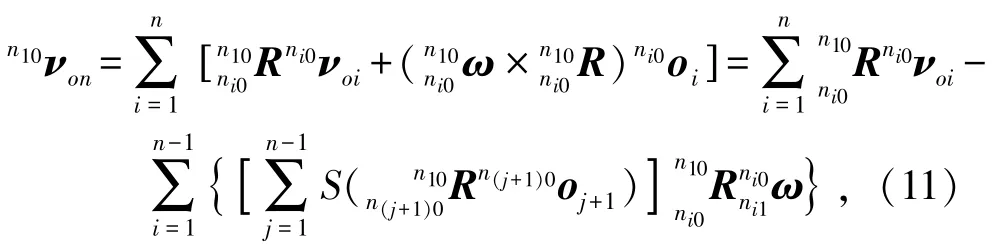
其中，n≥2，结合式（9），（11）可得

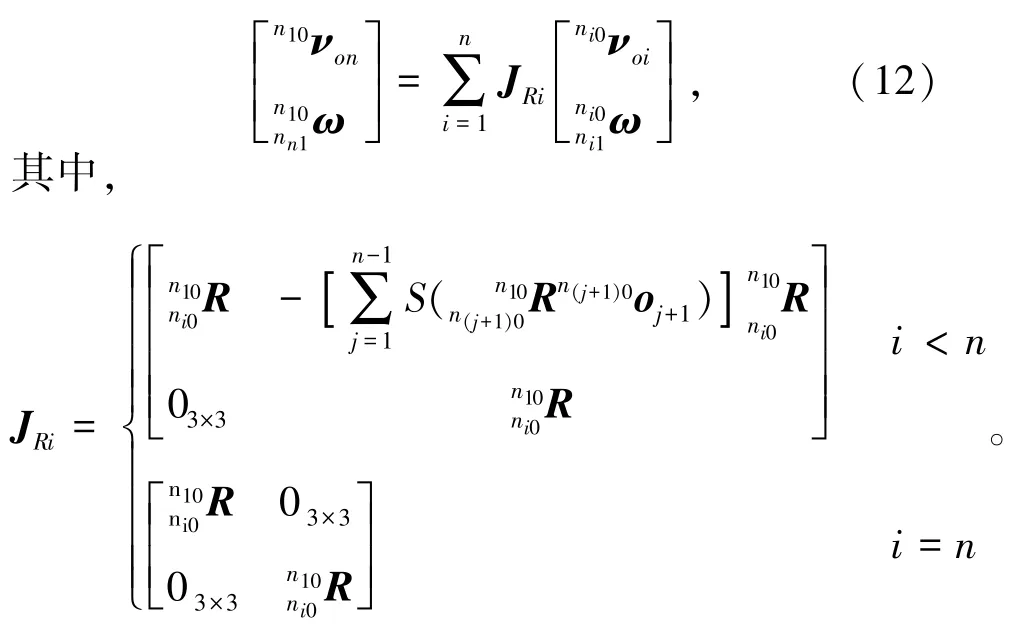
3 n（3⁃RPS）机构静力和刚度模型

对于第i个3⁃RPS机构，有

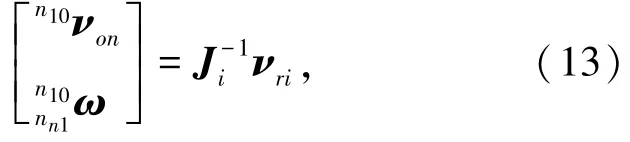
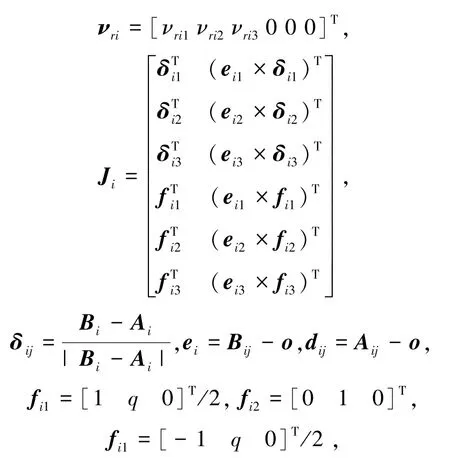
式中，Ji为第i个3⁃RPS机构的反解Jacobian矩阵。υrij（i＝1，2，…，n；j＝1，2，3）为沿着rrij的速度。结合式（12）和虚功原理可得

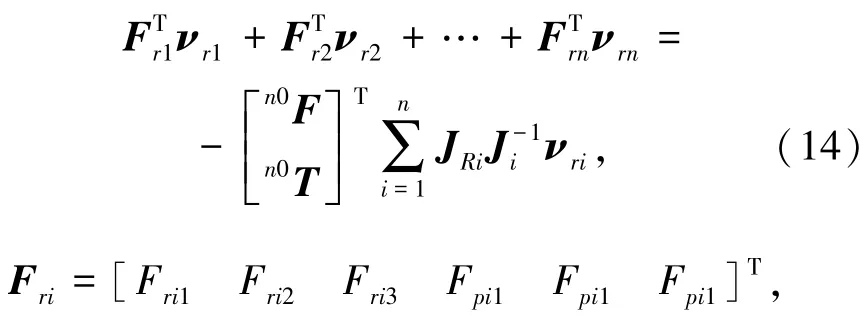
式中，Frij（i＝1，2，…，n；j＝1，2，3）是第i个3⁃RPS机构中的沿着rij的驱动力。Fpij是第i个3⁃RPS机构中的过 rij上的球副平行于该分支 R副的约束力［12］。

由式（14），可得

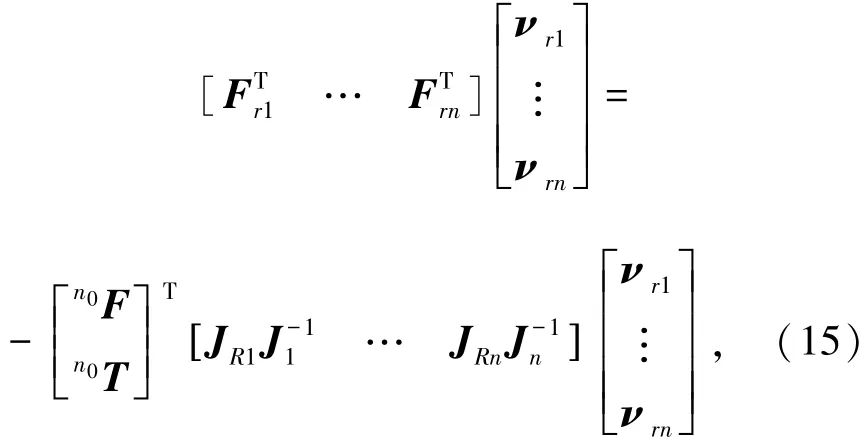
由式（15）可得

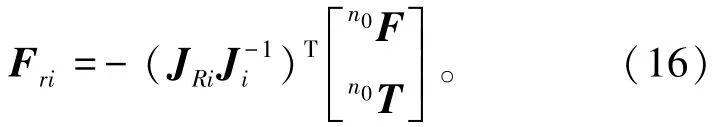
令Frij产生的拉伸变形为δdrij，可得

Fpij（i＝1，2，…，n；j＝1，2，3）在RPS分支上产生挠度变形（图2），设 δdpij为 Fpij产生的挠度变形，有

图2 约束力在RPS分支上产生的变形Fig.1 The deformation produced by constrained force for RPS leg

由式（17）、式（18），可得

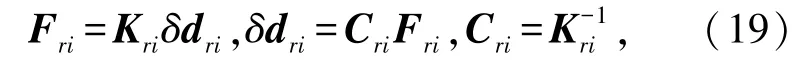
其中，

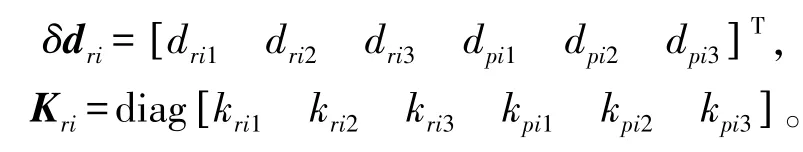
基于变形体的虚功原理，可得

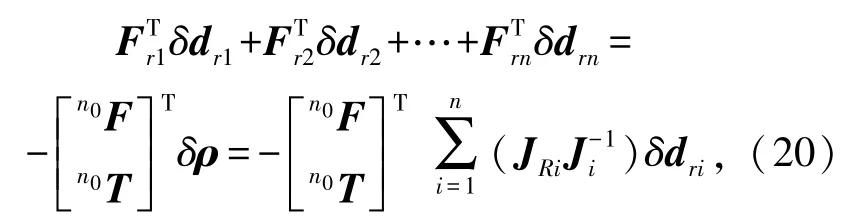
式中，ρ为末端平台的六维变形。由式（20），可得

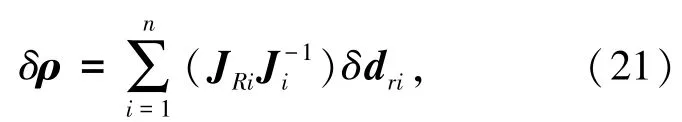
结合式（16），（19）和（21），可得

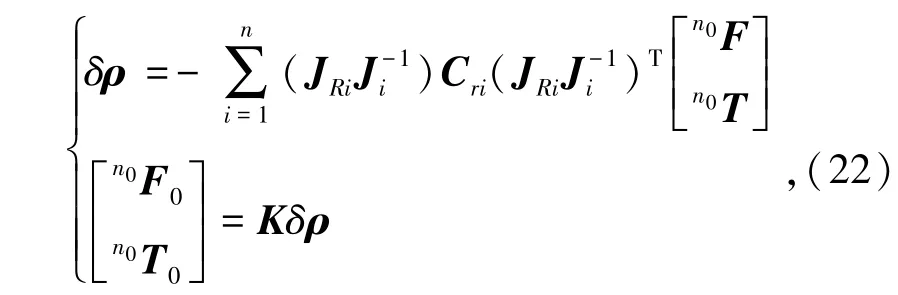
4 数值算例

4.1 n（3⁃RPS）机构静力和刚度计算

分别以2（3⁃RPS）和3（3⁃RPS）机构为研究对象进行数值计算。机构中各独立3⁃RPS机构的结构尺寸参数如表1所示。其中3（3⁃RPS）机构的第1、2独立机构与2（3⁃RPS）机构的第1、2独立机构尺寸相同。

给定两机构末端负载为AFod＝［－20－30－60］TN，ATod＝［0 0 0］TN·m。机构静力学计算结果如表2所示。

表1 第i个独立3⁃RPS机构尺寸参数Tab.1 Structure parameters of the i⁃th single 3⁃RPS manpulators

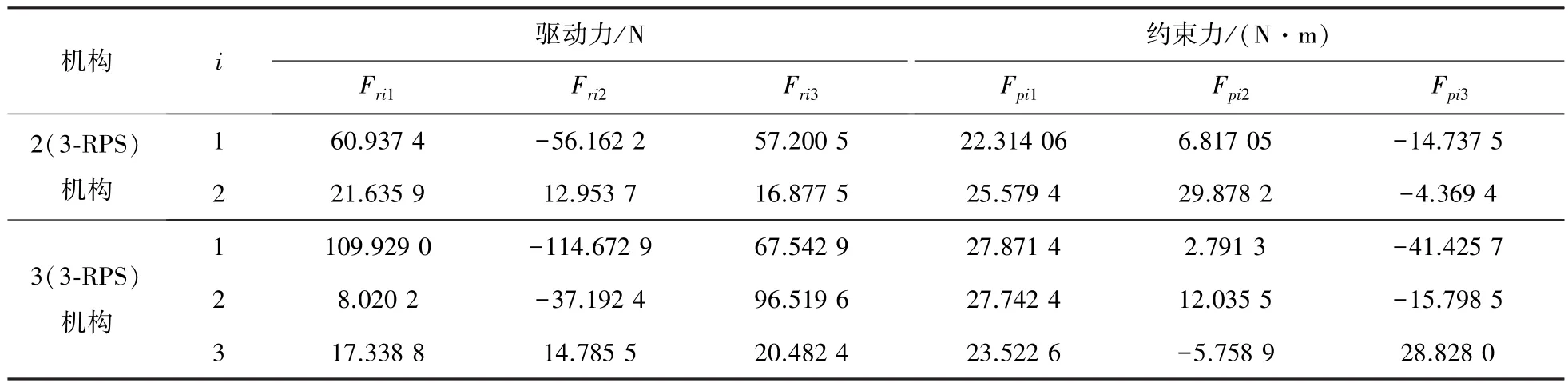
表2 2（3⁃RPS）和3（3⁃RPS）机构所受驱动力和约束力Tab.2 Active force and constraint force of the 2（3⁃RPS）and 3（3⁃RPS）manipulators

各机构的一些相关参数为Sij＝7.065×10－4m2，E＝2.11×1011N／m2，I＝1.256×10－7m4。2（3⁃RPS）机构和3（3⁃RPS）中主动力产生的沿驱动杆的拉伸变形和约束力产生的挠度变形如表3所示。

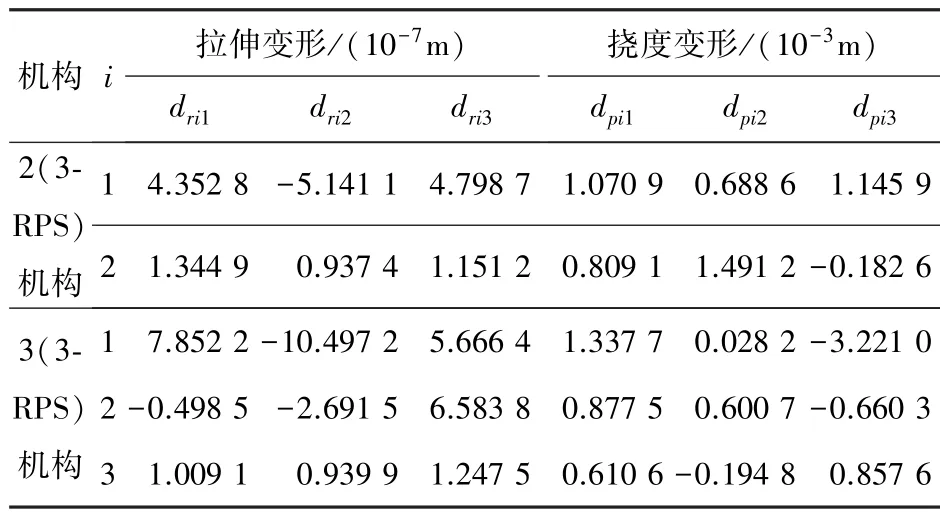
表3 2（3⁃RPS）机构和3（3⁃RPS）机构的分支变形Tab.3 The leg deformations of the 2（3⁃RPS）and 3（3⁃RPS）manipulators

2（3⁃RPS）机构和3（3⁃RPS）机构末端六维变形如表4所示。

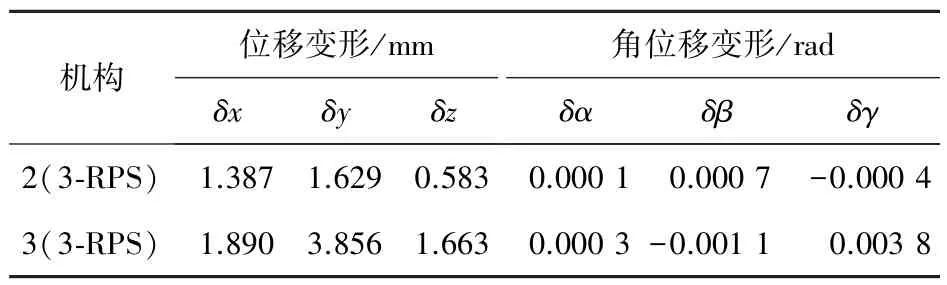
表4 2（3⁃RPS）机构和3（3⁃RPS）机构末端六维变形Tab.4 Deformations of the terminal platform of the 2（3⁃RPS）and 3（3⁃RPS）manipulators

4．2 n（3⁃RPS）机构有限元模型

为验证模型的有效性，建立两机构的有限元模型，在SolidWork软件中构造2（3⁃RPS）和3（3⁃RPS）机构的3维实体模型，两机构的尺寸参数和材料特性按照理论计算部分相应的参数设置，采用软件系统默认的网格划分，运行得到结果如图3和4所示。

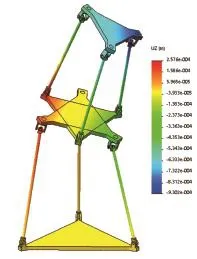
图3 2（3⁃RPS）机构有限元模拟结果Fig.3 Solved results of elastic deformations of 2（3⁃RPS）FE model

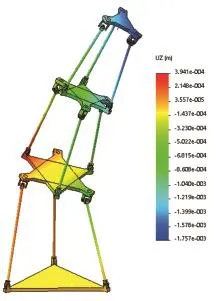
图4 3（3⁃RPS）机构有限元模拟结果Fig.4 Solved results of elastic deformations of 3（3⁃RPS）FE model

表5、表6是2（3⁃RPS）机构和3（3⁃RPS）机构末端变形的理论计算结果和有限元结果的对比。

表5 2（3⁃RPS）机构变形的计算结果和有限元结果对比Tab.6 Comparison of the deformation between the analytical result and the finite element model result for 2（3⁃RPS）manipulator

表6 3（3⁃RPS）机构变形的计算结果和有限元结果对比Tab.6 Comparison of the deformation between the analytical result and the finite element model result for 3（3⁃RPS）manipulator

有限元模拟结果和网格划分、边界条件、加载方式等有关，因此有限元模拟得到的结果只是一个近似的结果。通过对比表明，理论模型得到的机构末端3个方向的变形结果和有限元模拟结果基本一致。由此，仿真结果充分验证了刚度模型的正确性。

5 结论

1）对n（3⁃RPS）混联机构的速度传递关系进行了分析，为刚度模型建立奠定了基础性工作。

2）对n（3⁃RPS）混联机构来说，分支中存在拉伸变形和挠度变形，这些变形对机构末端的变形都有影响，机构的刚度矩阵为一6×6对称矩阵。

3）由于考虑了约束反力的因素，这种建立刚度模型的方法更符合实际，刚度模型的结果已经得到有限元验证，本文中的方法也适合其它混联机构。

［1］Merlet J P.Parallel robots［M］.London：Kluwer Academic Pub⁃lishers，2000.

［2］Huang Z，Li Q C.General Methodology for Type Synthesis of Low⁃er⁃Mobility Symmetrical Parallel Manipulators and Several Novel manipulators［J］.International Journal of Robotics Research，2002，21（2）：131⁃145.

［3］Gao F，Li W，Zhao X.New kinematic structures for 2⁃，3⁃，4⁃，and 5⁃dof parallel manipulator designs［J］.Mechanism and Machine Theory，2002，37（11）：1395⁃1411.

［4］Hu B，Lu Y，Yu J J，et al.Analyses of inverse kinematics，statics and workspace of a novel 3RPS⁃3SPR serial⁃parallel manipulator［J］.Open Mechanical Engineering Journal，2012，6（1）：65⁃72.

［5］Gallardo⁃Alvarado J，Posadas⁃García J.Mobility analysis and ki⁃nematics of the semi⁃general 2（3⁃RPS）series⁃parallel manipulator［J］.Robotics and Computer⁃Integrated Manufacturing，2013，29（6）：463⁃472.

［6］Zeng Q，Fang Y，Structural synthesis and analysis of serial⁃parallel hybrid mechanisms with spatial multi⁃loop kinematic chains［J］.Mechanism and Machine Theory，2012，49（3）：198⁃215.

［7］Gosselin C M.Stiffness mapping for parallel manipulators［J］. IEEE Transactions on Robotics and Automation，1990，6（3）：377⁃382.

［8］Joshi s，Tsai L W.A comparison study of two 3⁃DOF parallel ma⁃nipulators：one with three and the other with four supporting legs［J］.IEEE Transaction on Robotics and Automation，2003，19（2）：200⁃209.

［9］Klimchika A，Chablatb D，Pashkevicha A.Stiffness modeling for perfect and non⁃perfect parallel manipulators under internal and external loadings［J］.Mechanism and Machine Theory，2014，79（9）：1⁃28.

［10］Zhang D.On stiffness improvement of the Tricept machine tool［J］.Robotica，2005，23（3）：377⁃386.

［11］李剑锋，费仁元，范金红，等.具有大位置空间的3自由度并联机构运动性能分析［J］.机械工程学报，2007，43（8）：53⁃59.

［12］胡波，路懿.求解3⁃RPS并联机构刚度的新方法［J］.机械工程学报，2010，46（1）：24⁃29.

Statics and stiffness model of n（3⁃RPS）serial⁃parallel manipulators

HU Bo1，2，SONG Chun⁃xiao1，2，WANG An⁃dong1，2，CUI He1，2，LI Bo1，2，YU Jing⁃jing1，2
（1.Hebei Provincial Key Laboratory of Parallel Robot and Mechatronic System，Yanshan University，Qinhuangdao，Hebei 066004，China；2.Key Laboratory of Advanced Forging＆Stamping Technology and Science（Yanshan University），Ministry of Education of China，Qinhuangdao，Hebei 066004，China）

A statics and stiffness model of the n（3⁃RPS）serial⁃parallel manipulator is established.First，the transfer relation of ve⁃locity for the n（3⁃RPS）serial⁃parallel manipulator is analyzed based on the kinematics property.Second，the statics of n（3⁃RPS）serial⁃parallel manipulator is solved based on the principle of virtual work.Third，the stiffness model of the n（3⁃RPS）serial⁃parallel manipulator is established，and the deformation of this serial⁃parallel manipulator is solved.The finite element（FE）models of 2（3⁃RPS）and 3（3⁃RPS）serial⁃parallel manipulators are established，and the validity of the analytic model is verified by the simulation results.The methodology for establishing stiffness model of n（3⁃RPS）serial⁃parallel manipulator is also suitable for other serial⁃par⁃allel manipulators.

serial⁃parallel manipulator；statics；stiffness；deformation

TH112

A

10．3969／j．issn．1007⁃791X．2015．05．004

1007⁃791X（2015）05⁃0408⁃06

2014⁃10⁃27 基金项目：国家自然科学基金资助项目（51305382）；河北省高等学校科学技术研究优秀青年基金资助项目（YQ2013011）；燕山大学“新锐人才”工程支持计划项目

∗胡波（1982⁃），男，湖北襄阳人，博士，副教授，主要研究方向为并联机器人理论，Email：hubo＠ysu.edu.cn。