复杂多环路连杆机构曲柄判定的分支图识别法
2022-11-09聂良益丁华锋王君毕树生
聂良益 丁华锋 王君 毕树生
(1. 湖北理工学院 机电工程学院, 黄石 435003; 2. 中国地质大学(武汉) 机械与电子信息学院, 武汉 430074;3. 湖北工业大学 机械工程学院, 武汉 430068; 4. 北京航空航天大学 机械工程及自动化学院, 北京 100083)
连杆机构的曲柄指的是能够作整周转动的连架杆,其被广泛应用于航空航天领域中,如动力引擎中做往复运动的曲轴活塞机构、勘探小车的行走装置等。 对连杆机构设计来说,判断在杆件参数已知的连杆机构内是否存在曲柄,可以设计出满足功能和运动需求,且运动学性能优良、无运动缺陷的机构骨架,对机械设备的研制工作具有一定的指导意义。
连杆机构的曲柄研究工作最早起源于对平面4R 连杆机构运动分析的探讨,提出了著名的Grashof 定理[1]。 曲柄存在条件的核心是铰链转角范围的判定与机架的选择,然而Grashof 定理仅仅对平面4R 连杆机构适用,对于其他连杆机构曲柄判定无法适用,这引起了广大学者的研究兴趣。张全明等[2]根据原动件与机架组的极端条件和杆组适应性条件提出2-DOF 平面五杆的双曲柄存在的充要条件。 田汉民等[3]在Grashof 定理的基础上研究了2-DOF 五杆机构的曲柄存在情况。廖汉元等[4]应用机架变换法导出了2-DOF 铰链五杆机构的全部类型,判断了机构的类型。 Tsai和Ting[5]依靠传动角的概念针对两输入相邻情况下的平面五杆机构提出了相应的运动准则,用于连杆机构的完全旋转特性判别。 Ting[6]拓展了Grashof 定理,得到了关于单闭环N杆的曲柄存在条件,在重新定义机构长短杆的基础上,提出3 条关于曲柄存在的准则。 王君等[7-8]建立了连杆机构的环路方程,通过判别式求解得到Stephenson 六杆、Watt 六杆、齿轮五杆机构的死点情况,从而判断其相应机构的完全旋转特性。 郭晓宁和褚金奎[9]提出了距离曲线-限制线回路分析法,给出Stephenson II 型六杆机构的曲柄存在条件。 宋杰等[10]提出了虚杆概念,将六杆机构等效为四杆杆链,分析了平面3-DOF PRR-RRP 型六杆机构的曲柄存在条件。 戴建生和Shah[11]提出了一种通过工作区间分解,将连杆机构的可旋转性特性用于分析串联机械臂的定向能力的方法。
根据上述文献可知,N 杆旋转定理很好地解决了单闭环连杆机构的曲柄判定问题,但针对仅含有转动副的多环路连杆机构的曲柄存在问题,虽然已有不少研究方法,但其大多仅针对特定机构,适用范围小,通用性较差。 因此,本文提出了分支图识别法。 该方法通过利用连杆机构运动分支识别图与杆件的关系不等式对只含有转动副的单闭环、复杂多环路连杆机构内的曲柄进行判定,通用性好,适用范围广。
1 杆件关系不等式
1.1 Grashof 定理
以图1 中所示平面4R 连杆机构举例说明,l1、l2、l3、l4分别表示杆1、杆2、杆3、杆4 的杆长参数,由Grashof 定理,即最短杆与最长杆杆长之和小于或等于中间杆的杆长长度之和(式(1)),可确定该平面4R 连杆机构的曲柄存在情况。

图1 平面4R 连杆机构Fig.1 Planar four-bar linkage
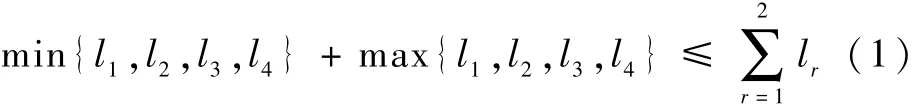
最短杆的间隔杆为固定机架时,为双摇杆机构(见图2(a));最短杆相邻的连杆为固定机架时,为曲柄摇杆机构(见图2(b));最短杆为固定机架时,为双曲柄机构(见图2(c))。
对于最短杆与最长杆之和大于中间杆的长度和,则无论连杆机构内任何连杆被作为固定机架,该连杆机构内均不存在曲柄,为双摇杆机构;最短杆与最长杆之和等于中间杆的长度和,连杆机构内存在运动失控的死点位置。 因此,上述2 种情况均不作讨论。
图2 中虚线为平面4R 连杆机构运动的极限位置,且各个机构的杆长参数如表1 ~表3 所示。
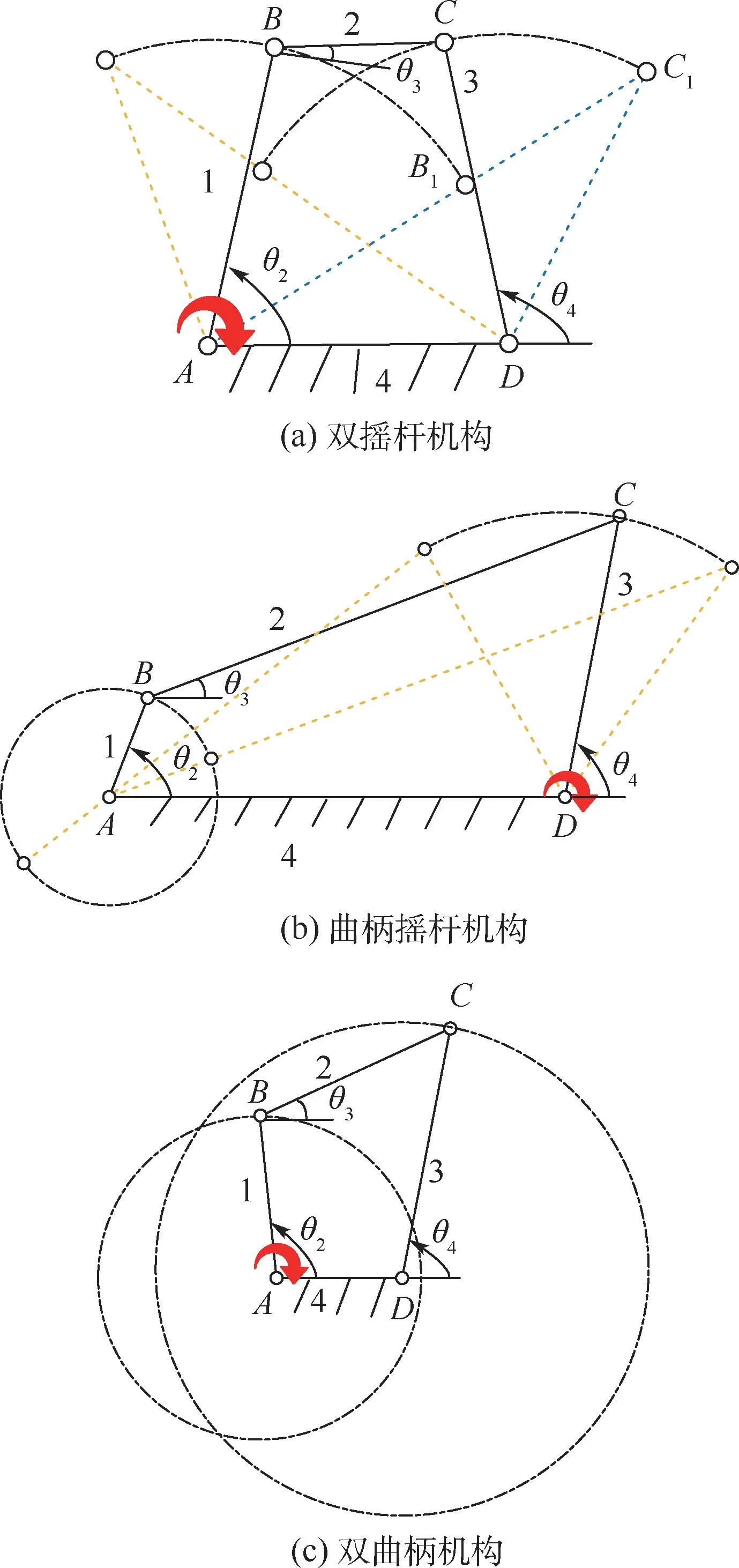
图2 平面4R 连杆机构曲柄存在情况Fig.2 Cranks of planar four-bar linkages

表1 图2(a)双摇杆机构杆长参数Table 1 Parameters of double rocker linkage in Fig.2(a)

表2 图2(b)曲柄摇杆机构杆长参数Table 2 Parameters of crank-rocker linkage in Fig.2(b)

表3 图2(c)双曲柄机构杆长参数Table 3 Parameters of double crank linkage in Fig.2(c)
1.2 N 杆旋转定理
Grashof 定理应用对象单一,为解决这一缺陷,N 杆旋转定理重新定义了长短杆,并给出了仅含转动副的单闭环连杆机构的曲柄判定准则[6],以图3 所示的2-DOF 5R 连杆机构曲柄判断说明。
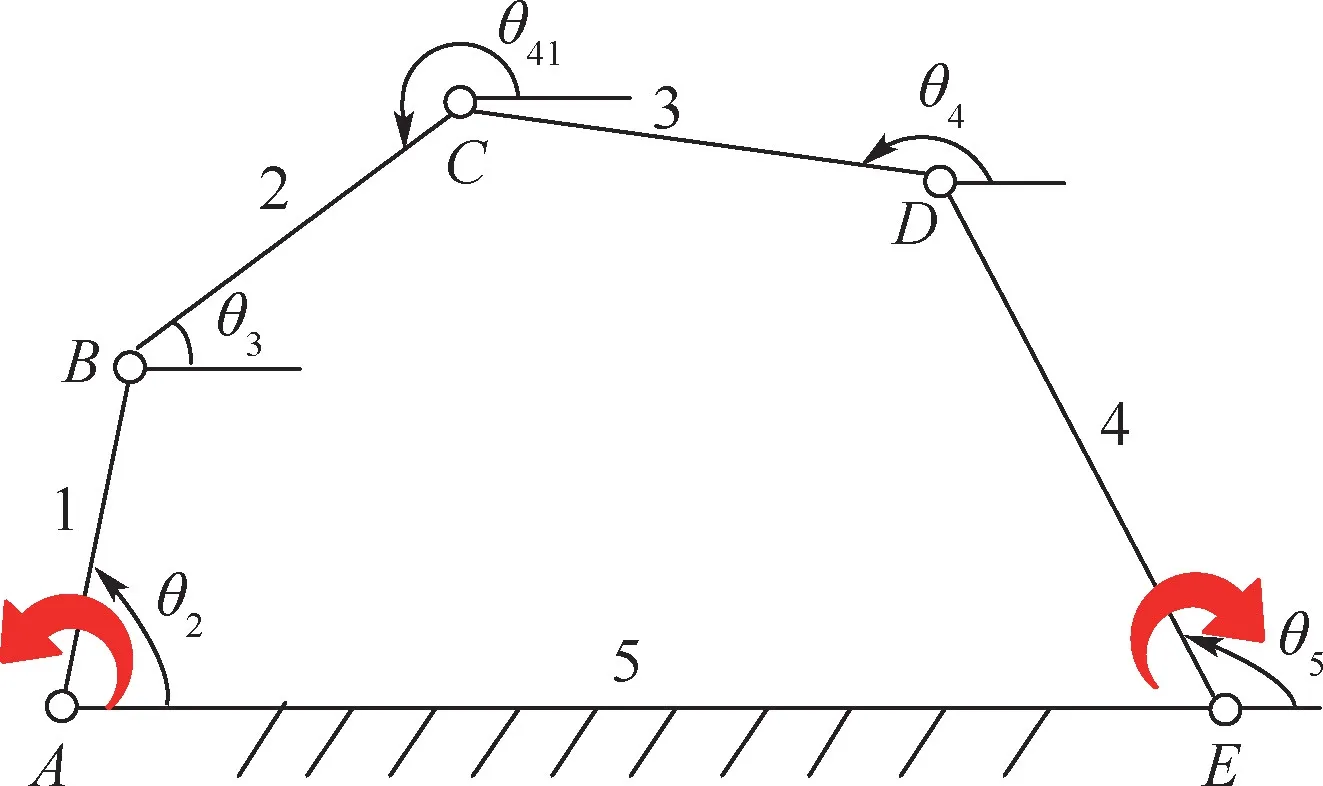
图3 平面5R 连杆机构Fig.3 Planar five-bar linkage
1.2.1N杆机构杆件关系
1) 条件设定。 假定在闭环单链N杆机构中,所有铰接关节均为转动副,规定所有杆全是简单二力杆,用li(i=1,2,…,n)表示连杆机构内杆件的杆长,其大小为两旋转副中心的距离,且令连杆机构中各杆件间杆长关系满足l1≤l2≤…≤ln-1≤ln。
2) 机构装配的充要条件。 在任意N(N≥3)连杆机构中,杆长间关系必须满足非最长杆的所有杆件杆长之和大于或等于最长杆杆长时,连杆机构才能被成功装配,即满足如下不等式:

3) 定义连杆机构内长短杆。
①短杆。 在N杆机构中,杆长与最长杆杆长之和小于或等于其他杆件杆长之和的连杆,也就是满足如下不等式,即为短杆。

②长杆。 在N杆机构中,杆长与最长杆杆长之和大于其他杆件杆长之和的连杆,也就是满足如下不等式,即为长杆。

值得注意的一点是,当n=3,则连杆机构内每个杆均可作为长杆。
1.2.2N杆机构曲柄判断定理
定理1 在闭环单链N杆机构中有且仅有两相邻杆旋转角度能达到0°与180°时,两杆之间才可能存在曲柄。
定理2 在闭环单链N杆机构中短杆与N杆中其他任意连杆存在整转副,即可能形成曲柄,若该连杆为连架杆,则其确定为该机构的曲柄,长杆不能与N杆中其他任意长杆存在整转副,即不能形成曲柄。
1.2.3 连杆机构的3 种分类
由连杆机构杆件满足不同的杆长关系,可以将闭环单链N杆机构分成3 类:
1) 当连杆机构杆长关系满足不等式(5),为第Ⅰ类连杆。
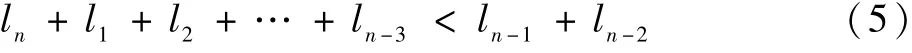
由不等式(2)、(5)可推导出,对于属于第Ⅰ类连杆机构的杆件,也满足l1+l2+ … +ln-3≤ln-2≤ln-1≤ln。 也就是说,第Ⅰ类连杆中有3 个长杆,而任意两长杆之间的旋转角度都不能达到0°与180°,即不存在杆件间共线与折叠的情况,依据定理1,若输入在三长杆两端,则连杆机构中无曲柄存在,换句话说,要想机构可能存在曲柄,则至少有一个输入在短杆上,如图2(b)所示平面4R 曲柄摇杆机构即为这种情况。
2) 当连杆机构杆长件关系满足不等式(6),为第Ⅱ类连杆。
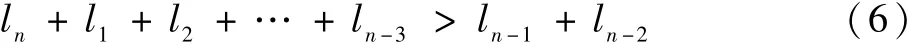
由不等式(6)可得,在第Ⅱ类连杆机构中,任意两长杆可能能达到共线或折叠的情况(180°或者0°),但是关节的旋转角度范围不能同时包含0°与180°,依据定理1,满足该类条件的连杆机构中无曲柄存在。
3) 当连杆机构杆长件关系满足等式(7),为第Ⅲ类连杆。
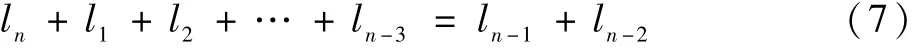
与第Ⅰ类连杆机构对比,在第Ⅲ类连杆机构中,由等式(7)可得,连杆机构可能存在曲柄,但也可能存在使机构失去控制的死点位置,因此一般不作讨论。
1.2.4 2-DOF 5R 连杆机构曲柄判别
为了分析方便与装配要求,2-DOF 5R 连杆机构的杆长间关系需满足如下条件:

图4 为平面5R 连杆机构相邻杆满足杆件间关系存在曲柄的可能情况。 依据定理1 和定理2,当l5+l1≤l2+l3+l4时,杆1 与任何杆相邻都能形成整转副(可能曲柄,进一步确定,取决杆1是否为机构的连架杆,下同);当l5+l1>l2+l3+l4时,机构内部杆件间均无法形成曲柄;当l5+l2≤l1+l3+l4时,杆2 与任何杆相邻都能形成整转副;当l5+l2>l1+l3+l4时,杆2 不能和其他长杆形成曲柄;当l5+l3≤l1+l2+l4时,杆3 与任何杆相邻都能形成整转副;当l5+l3>l1+l2+l4时,杆3 不能和其他长杆形成曲柄;当l5+l4≤l1+l2+l3时,杆4 与任何杆相邻都能形成整转副;当l5+l4>l1+l2+l3时,杆4 与杆5 不能形成曲柄。
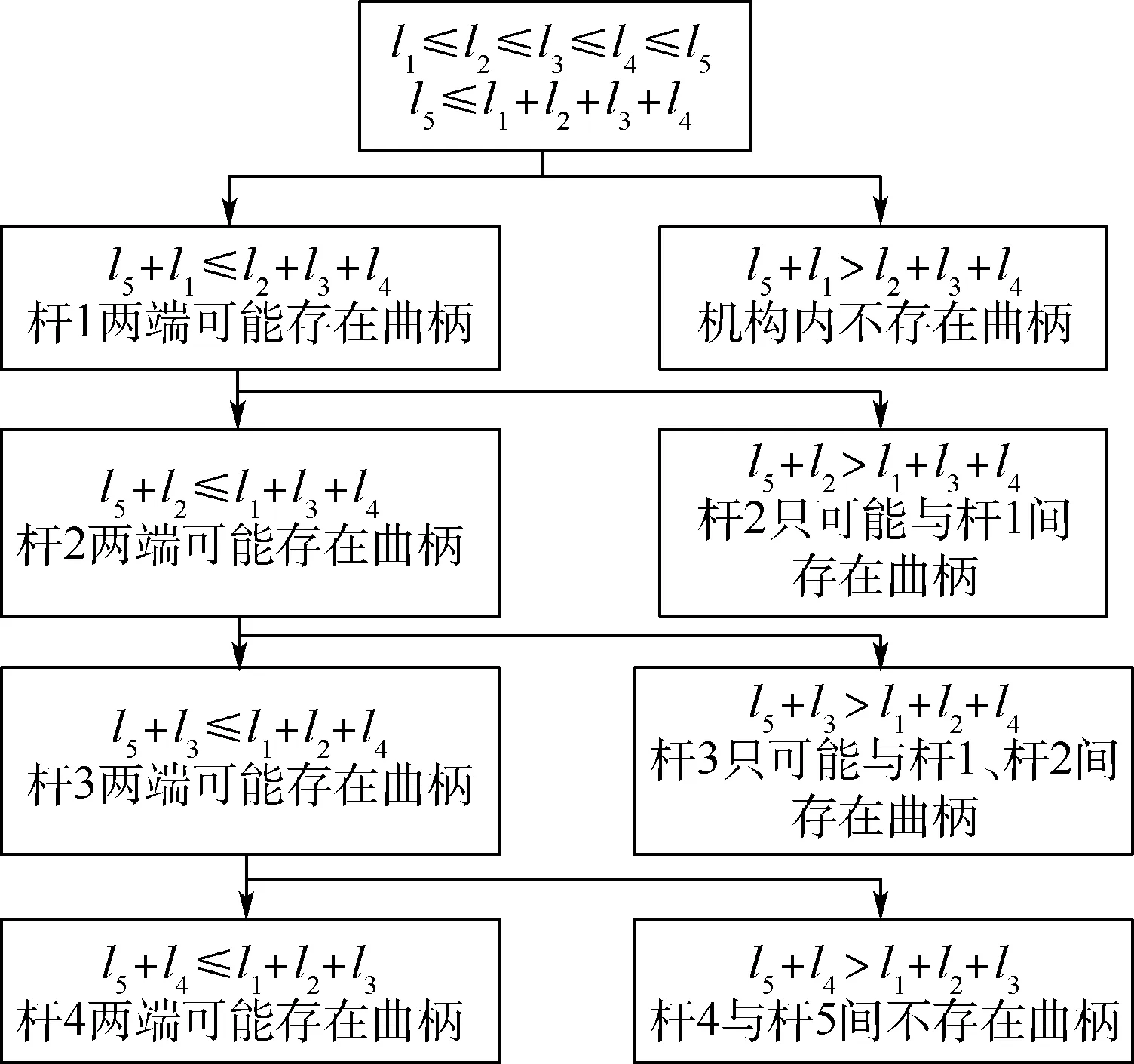
图4 平面5R 连杆机构曲柄判定流程Fig.4 Flowchart of crank judgement of planar five-bar linkage
图5 为4 种平面5R 连杆机构装配实例,其尺寸参数如表4 ~表7 所示。 在图5(a)、(b)中,杆长间关系满足l5+l2<l1+l3+l4与l5+l3<l1+l2+l4,因此,图5 (a)中连杆机构存在2 个曲柄与1 个整转副,分别在关节旋转副A、E、B处。 图5(b)中连杆机构存在2 个曲柄与2 个整转副,分别在关节旋转副A、E、B、D处。 图5(c)中杆长间关系满足l5+l1>l2+l3+l4,图5 (c)中连杆机构内无曲柄存在。 图5(d)中杆长关系满足l5+l3<l1+l2+l4与l5+l4>l1+l2+l3,因此,图5 (d)中连杆机构存在1 个曲柄与3 个整转副,分别在关节旋转副A、B、C、D。
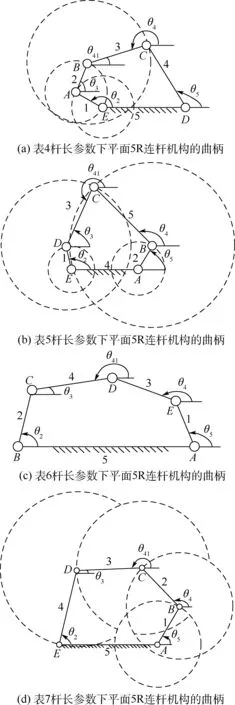
图5 平面5R 连杆机构的曲柄Fig.5 Cranks of planar five-bar linkages

表4 图5(a)平面5R 连杆机构杆长参数Table 4 Parameters of five-bar linkage in Fig.5(a)

表5 图5(b)平面5R 连杆机构杆长参数Table 5 Parameters of five-bar linkage in Fig.5(b)

表6 图5(c)平面5R 连杆机构杆长参数Table 6 Parameters of five-bar linkage in Fig.5(c)

表7 图5(d)平面5R 连杆机构杆长参数Table 7 Parameters of five-bar linkage in Fig.5(d)
2 曲柄判定分支图
分支识别图由机构的环路方程形成,包含连杆机构所有的运动信息,一般用来解决机构的分支与子分支识别问题[7-8,12-15],但本文中其被用于解决连杆机构曲柄判定问题,因为机构的分支识别图只与机构的杆长参数有关,与机构输入位置的选择无关,也就是使用曲柄判定分支图识别法无需指定机构的输入关节。
图6(a)、(b)为图2(a)平面4R 连杆机构关于关节角度θ2与关节角度θ3、θ4的分支识别图。在图6(a)中,关节角度θ2在[0°,A],[A,360°]范围内转动,关节角度θ3可以在[0°,360°]范围内转动,即整转副存在旋转关节B处。 在图6(b)中,关节角度θ2在[0°,C],[E,360°]范围内转动,关节角度θ4分别对应在[0°,D],[F,360°]范围内转动,即不存在曲柄。 由以上分析可证实该连杆机构为双摇杆机构。
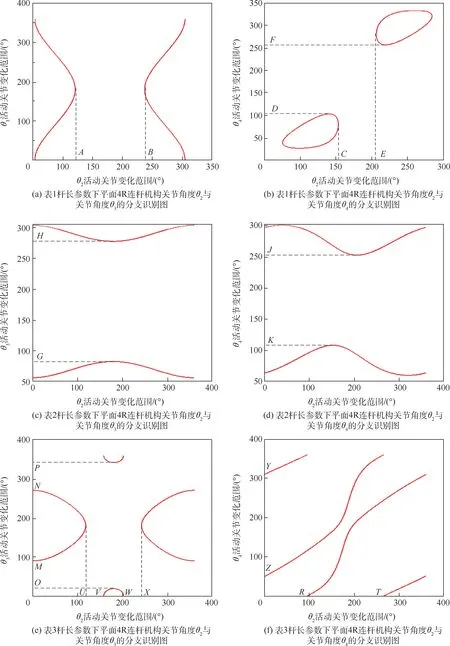
图6 平面4R 连杆机构曲柄分支识别图Fig.6 Crank judgement of planar four-bar linkage with branch graph
图6(c)、(d)为图2(b)平面4R 连杆机构关于关节角度θ2与关节角度θ3、θ4的分支识别图。在图6(c)中,关节角度θ2可以在[0°,360°]范围内转动,关节角度θ3可以在[0°,G],[H,360°]范围内转动,即曲柄存在旋转关节A处。 在图6(d)中,关节角度θ2可以在[0°,360°]范围内转动,关节角度θ4分别对应在[0°,K],[J,360°]范围内转动,也就是仅关节角度θ2能做整转运动。 综上,该机构为曲柄摇杆机构。
图6(c)、(d)为图2(c)平面4R 连杆机构关于关节角度θ2与关节角度θ3、θ4的分支识别图。在图6(e)中,关节角度θ2可以在[0°,U],[V,W],[X,360°]范围内转动,关节角度θ3分别在[M,N],[0°,O]/[P,360°]范围内转动(均不能形成整转运动)。 在图6(f)中,关节角度θ2可以在[0°,T],[T,360°]范围内转动,关节角度θ4分别对应在[Z,360°],[0°,Z]范围内转动,即关节角度θ2、θ4能做整转运动。 综上,该机构是双曲柄机构。
3 平面5R 连杆机构曲柄判定
图7(对应图5(a)平面5R 连杆机构)为关节角度θ2与关节角度θ3、θ41、θ4、θ5的分支识别图。 通过分 析 可 得,关 节 角 度θ2、θ3、θ41可 以 做整转运动,而关节角度θ4、θ5只能做一定角度内的往复运动,因此该机构的曲柄存在于关节旋转副E处。
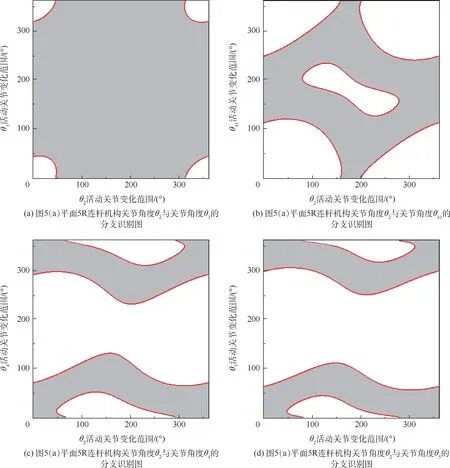
图7 平面5R 连杆机构曲柄分支识别图(对应图5(a)平面5R 连杆机构)Fig.7 Crank judgement of planar five-bar linkage with branch graph (Fig.5(a))
图8(对应图5(b)平面5R 连杆机构)为关节角度θ2与关节角度θ3、θ41、θ4、θ5的分支识别图。通过分析可得,关节角度θ2、θ3、θ4、θ5可以做整周运动,而关节角度θ41只能做[45°,320°]的往复运动,因此该机构的曲柄存在于关节旋转副E、A处。
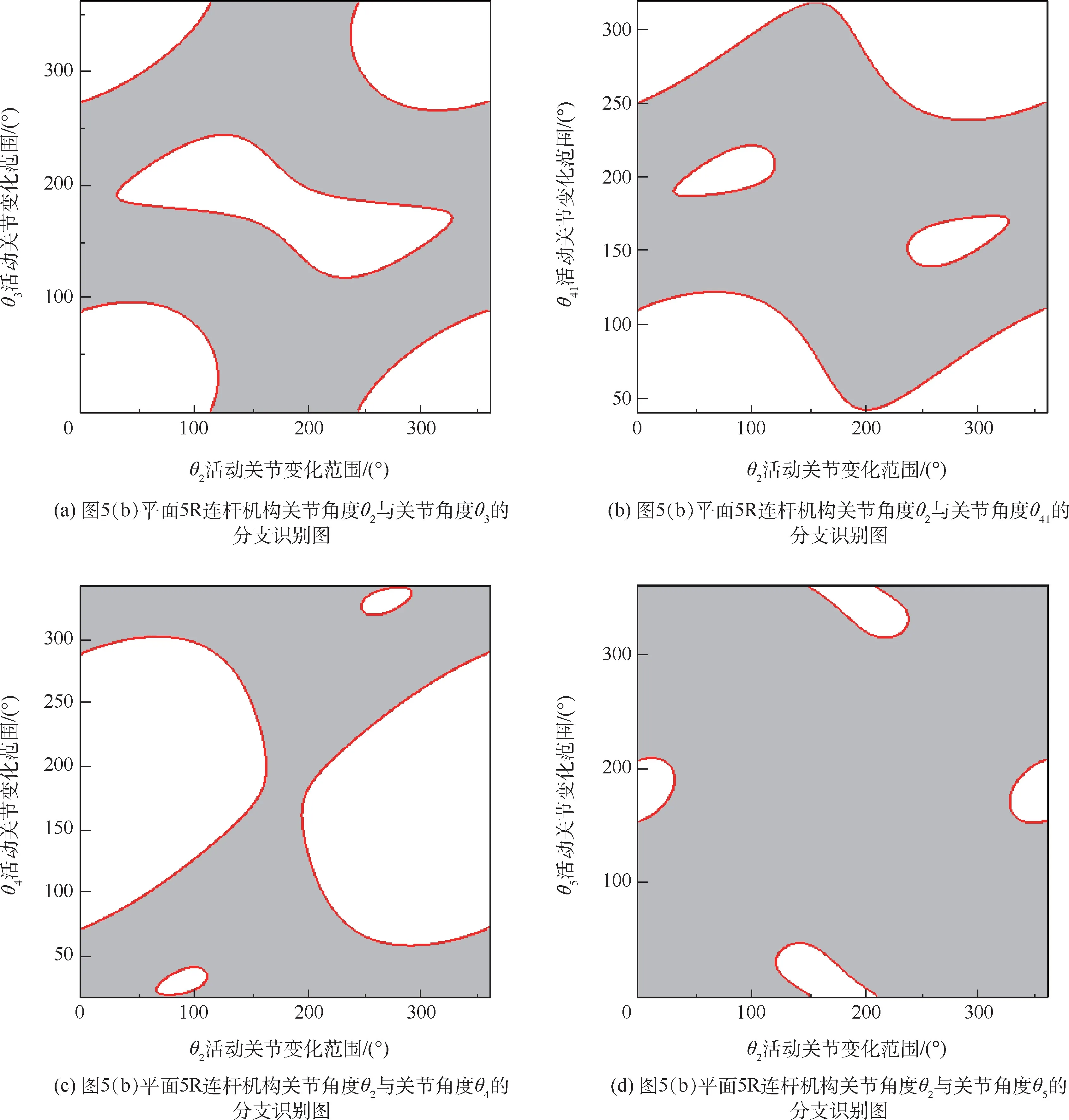
图8 平面5R 连杆机构曲柄分支识别图(对应图5(b)平面5R 连杆机构)Fig.8 Crank judgement of planar five-bar linkage with branch graph (Fig.5(b))
图9(对应图5(c)平面5R 连杆机构)为关节角度θ2与关节角度θ3、θ41、θ4、θ5的分支识别图。通过分析可得,关节角度θ2、θ3、θ4、θ41、θ5均只能在一定角度范围的往复运动,因此该机构内曲柄不存在。
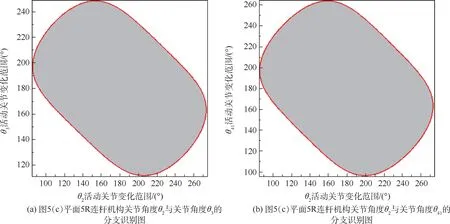

图9 平面5R 连杆机构曲柄分支识别图(对应图5(c)平面5R 连杆机构)Fig.9 Crank judgement of planar five-bar linkage with branch graph (Fig.5(c))
图10(对应图5(d)平面5R 连杆机构)为关节角度θ2与关节角度θ3、θ41、θ4、θ5的分支识别图。 通过分析可得,关节角度θ3、θ4、θ41、θ5可以做整转运动,而关节角度θ2只能做一定角度范围的往复运动,因此该机构的曲柄存在于关节旋转副A处。
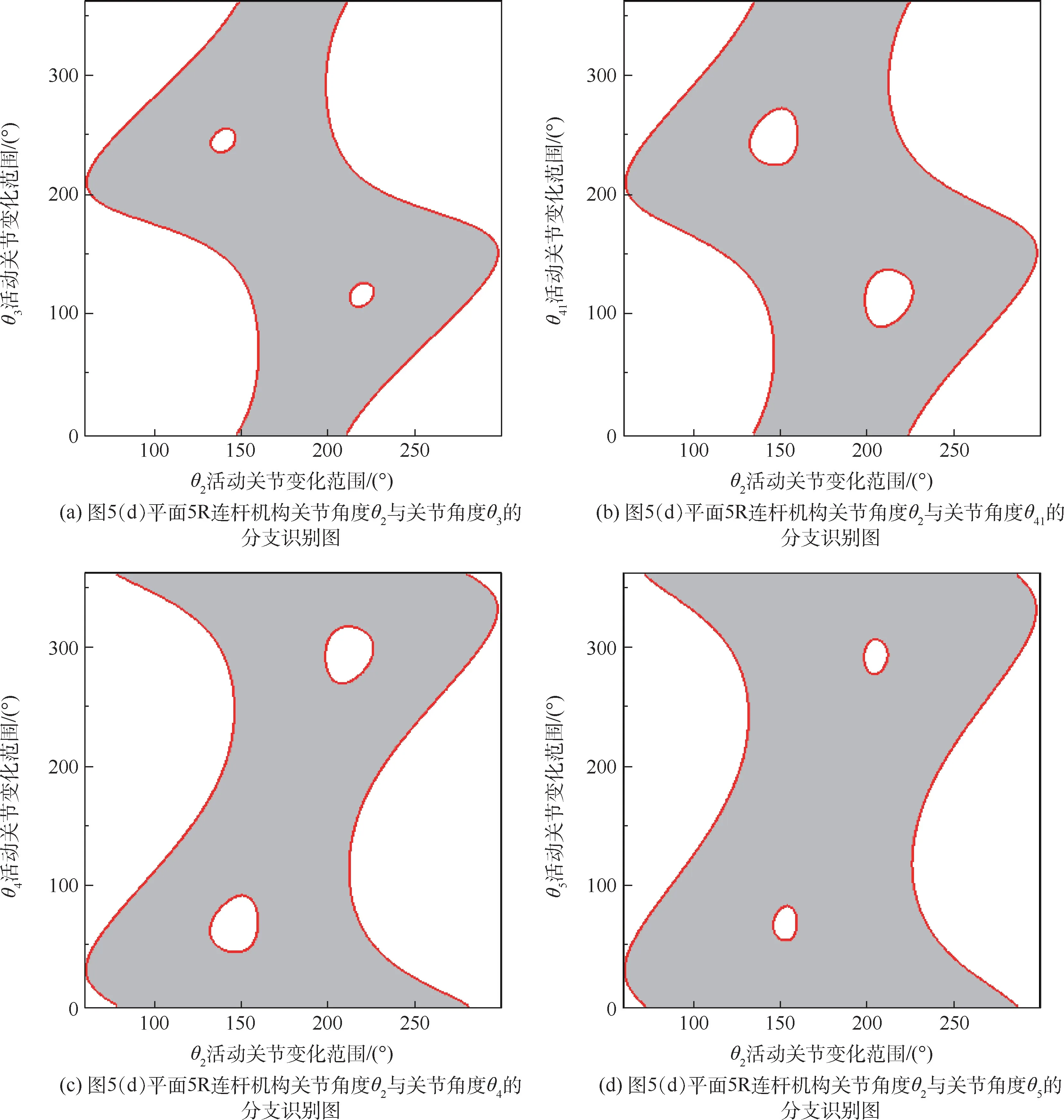
图10 平面5R 连杆机构曲柄分支识别图(对应图5(d)平面5R 连杆机构)Fig.10 Crank judgement of planar five-bar linkage with branch graph (Fig.5(d))
4 复杂多环路连杆机构曲柄判定
复杂多环路连杆机构是由多个简单的闭环单链耦合而成,如Stephenson 六杆、2-DOF 七杆机构、1-DOF 八杆机构等,其运动由多个环路耦合共同决定,运动情形较为复杂,曲柄问题难以研究。由连杆机构分支识别可知,若多环连杆机构内存在分支点,即机构可连续运动的区域被隔断[8],也就是大多数多环连杆机构内部是不存在曲柄的。反之,如何保证多环连杆机构在输入关节做整转运动成为一个难点。 针对这一问题,本文提出了关于2 条多环连杆机构存在曲柄的充分条件。
充分条件1 在所有耦合环路链中,杆件间杆长关系必须满足闭环单链曲柄存在条件,且作整转运动的旋转关节存在位置重合。
充分条件2 在所有耦合环路链中,在对应分支识别图中不存在分支点。
仅含转动副的Stephenson 六杆机构是较为简单的多环路连杆机构,其由一个闭环4R 单链与一个闭环5R 单链耦合而成。 本文以仅含转动副的Stephenson 六杆机构为例,解释复杂多环路连杆机构的曲柄判定问题。 依据仅含转动副的Stephenson 六杆机构中输入在不同环路链中其运动特性不同,将该机构内曲柄存在的问题按输入在四链环路中及输入在五链环路中分别讨论。
1) 输入在四链环路中
在图11 所示Stephenson 六杆机构中,当给定输入关节角度为θ2时,连杆机构由一个四链环路ABCD与一个五链环路ABEFG耦合而成。 即除装配条件外,四链环路ABCD与五链环路ABEFG中杆长关系需满足l41+l44<l42+l43,l51+l52+l55<l53+l54(l4i表示四链环路中的杆长,l5i表示五链环路中的杆长,i=1,2,3,4,5),且两环路链中关节角度θ2转动范围均为[0°,360°]。 在Stephenson 六杆机构分支识别图中,不存在分支点,即Stephenson 六杆机构的四链环路ABCD的关节旋转空间被包含在五链环路ABEFG的关节旋转空间内部,连杆机构的运动完全受四链环路的影响,如图12 所示,参数如表8 所示。
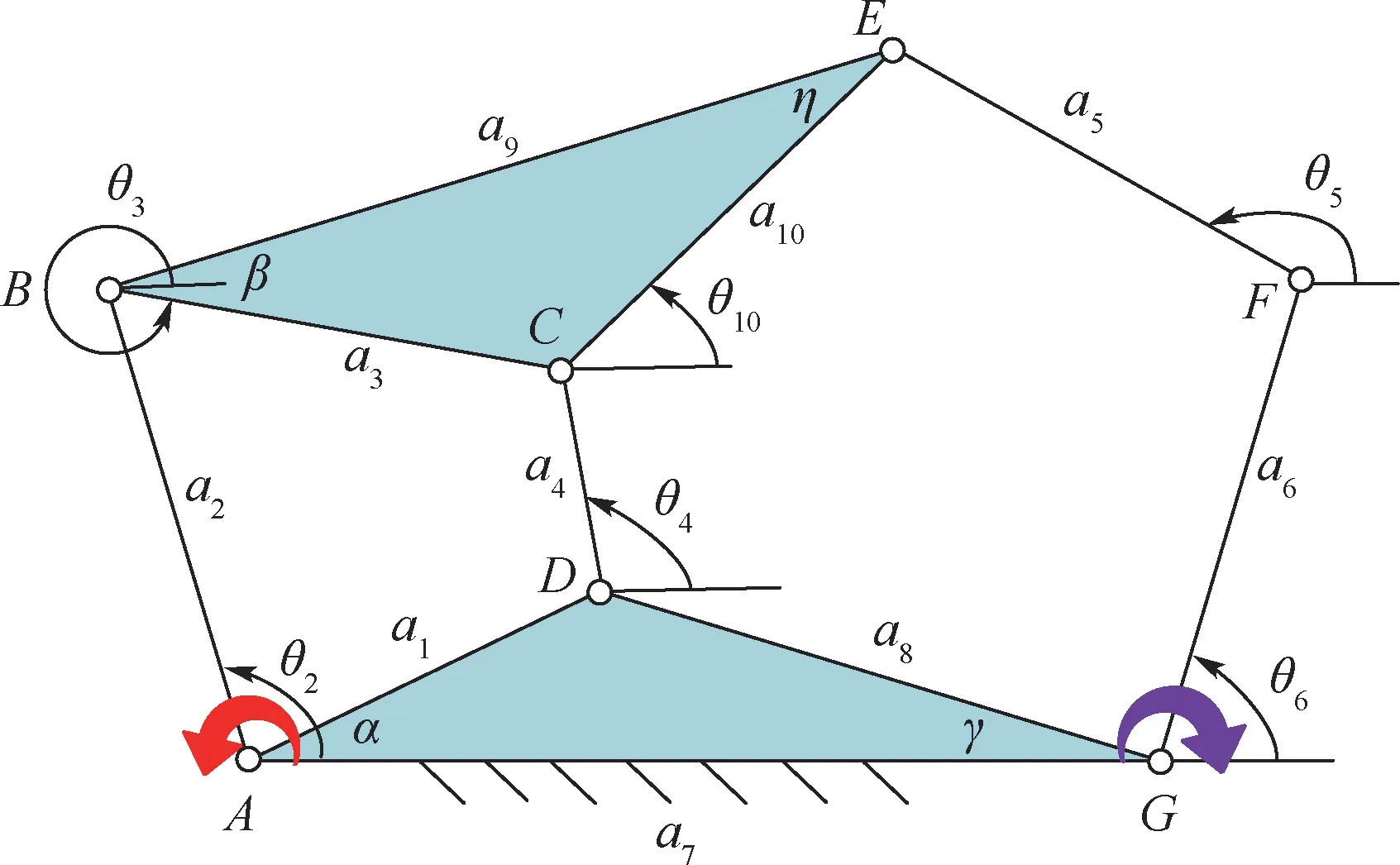
图11 Stephenson 六杆机构Fig.11 Stephenson six-bar linkage
由表8 中参数可得,四链环路ABCD中a2>a3>a1>a4,且a1+a3>a2+a4,令l44、l43、l42、l41分别为a2、a3、a1、a4,即l42+l43>l44+l41,连杆机构内存在曲柄。 但在Stephenson 六杆中,a1(满足不等式l44+l42>l43+l41)与a2均为长杆,其杆件间无法形成曲柄(见图12)。

图12 Stephenson 六杆机构曲柄分支识别图(四链环路输入)Fig.12 Branch graph for crank judgement of Stephenson six-bar linkage (input joint in four-bar loop)

表8 图12 Stephenson 六杆机构杆长对应参数Table 8 Parameters of Stephenson six-bar linkage in Fig.12
如要关节输入位置做整转运动,则a1与a2中需有短杆,又a2与五链环路ABEFG有关,因此对调表8 中a4与a1参数。 在五链环路ABEFG中,a6>a9≥a5>a2>a7且a9+a5<a6+a2+a7(由图8 灰色关节旋转空间所示,此时五链环路中也存在曲柄,但这是个例[16]不具有普适性),不满足充分条件1,依照曲柄存在关系式与长短杆定义,短杆两端可能存在曲柄,因此五链环路ABEFG参数调整如表9 所示,分支识别图如图13 所示,可知连杆曲柄在关节旋转副A处。
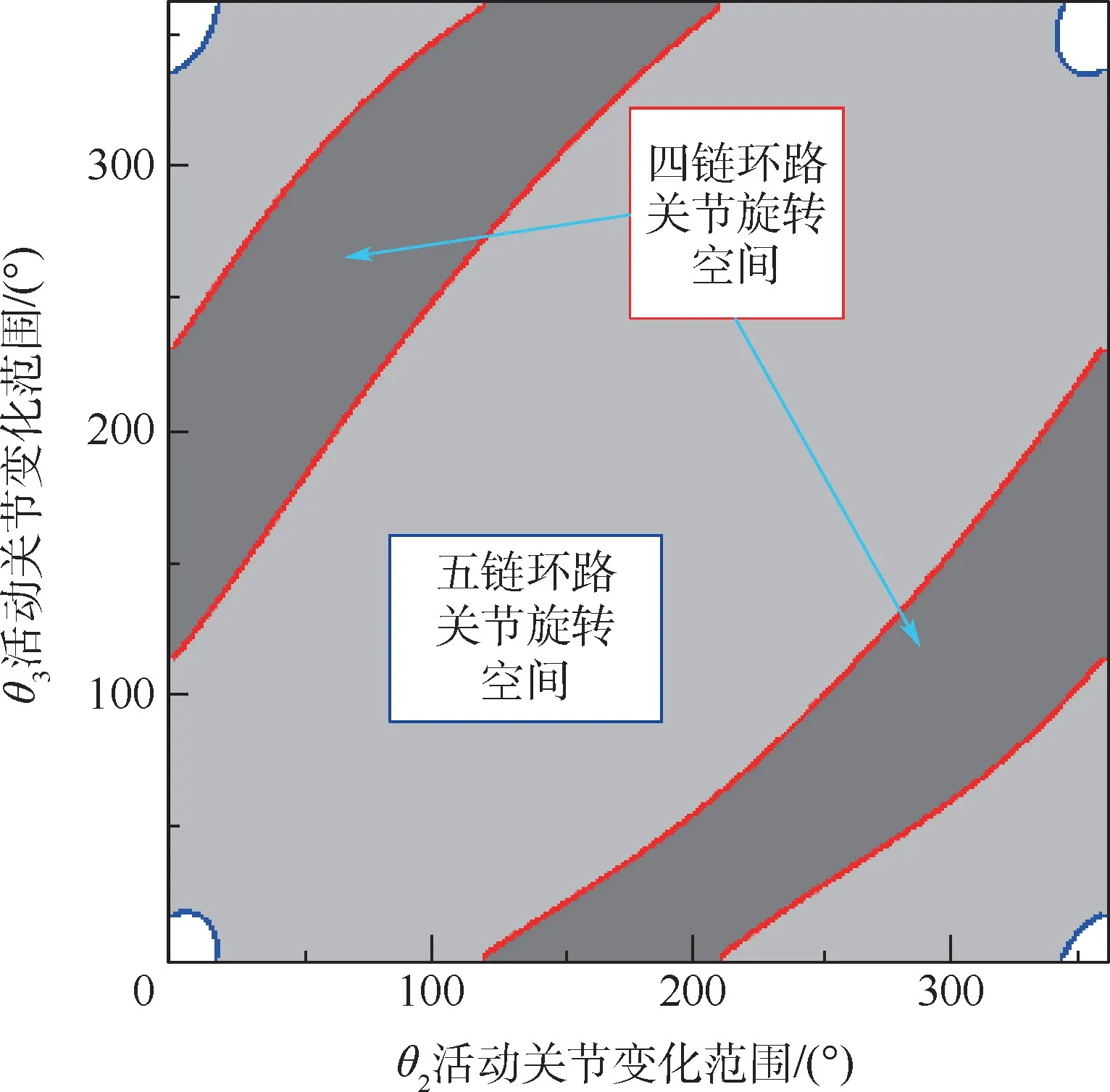
图13 Stephenson 六杆机构输入θ2 曲柄分支识别图(四链环路输入)Fig.13 Crank judgement of Stephenson six-bar linkage using branch graph with input angle θ2
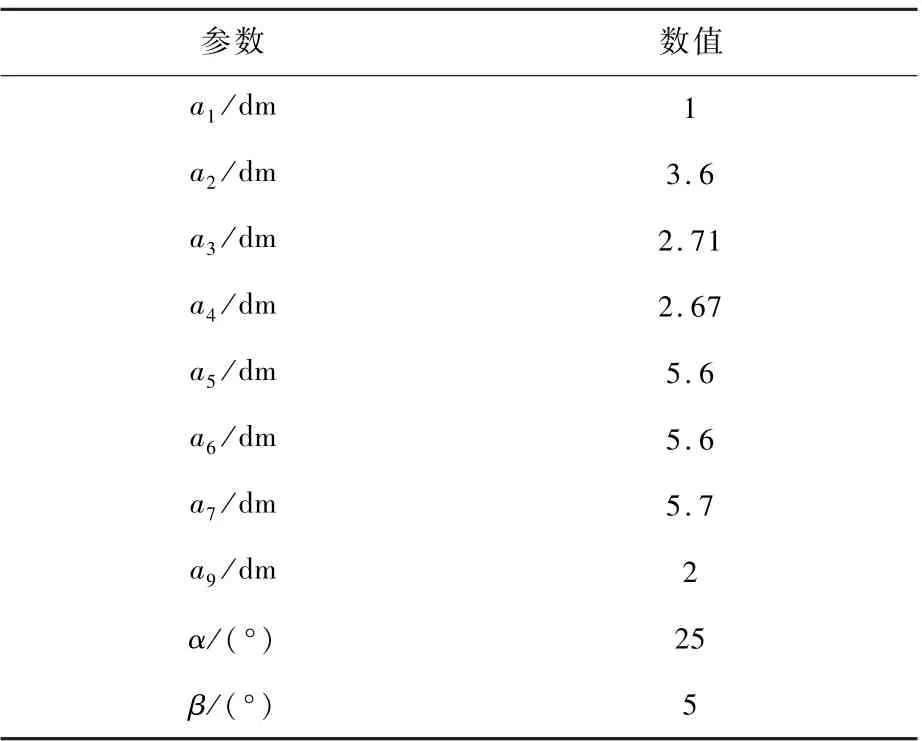
表9 图13 Stephenson 六杆机构输入θ2 曲柄对应参数Table 9 Parameters of Stephenson six-bar linkage with input joint θ2 in Fig.13
2) 输入在五链环路中
当给定输入关节角度为θ6时,连杆机构由2 个五链环路ABEFG与DCEFG耦合而成。 即除装配条件外,五链环路ABEFG与DCEFG中杆长关系需先满足l151+l152+l155<l153+l154,l251+l252+l255<l253+l254(l15i、l25i表示五链环路中的杆长,i=1,2,3,4,5),且两环路链中关节角度θ6转动范围均为[0°,360°],在Stephenson 六杆机构分支识别图中,不存在分支点,即Stephenson 六杆机构的一个五链环路的关节旋转空间被包含在另一五链环路的关节旋转空间内部,连杆机构的运动完全受其中一个五链环路的影响,如图14 所示,参数如两环路链均不满足必要充分条件1,依照曲柄存在关系式与长短杆定义,且短杆两端可能存在曲柄,两五链环路参数调整如表11 所示,分支识别图如图15 所示。 可知,连杆曲柄在关节旋转副G处。

图14 Stephenson 六杆机构分支识别图(五链环路输入)Fig.14 Branch graph of Stephenson six-bar linkage with input angle in five-bar loop
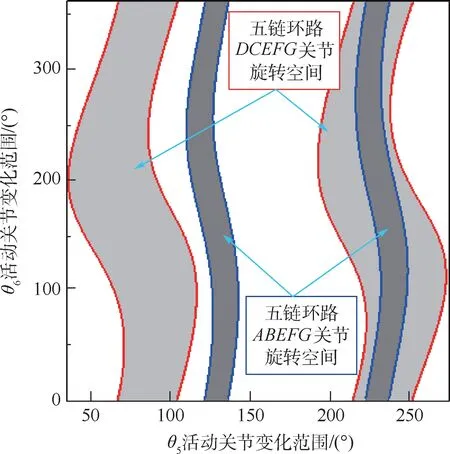
图15 Stephenson 六杆机构输入θ6 曲柄分支识别图(五链环路输入)Fig.15 Crank judgement of Stephenson six-bar linkage using branch graph with input angle θ6
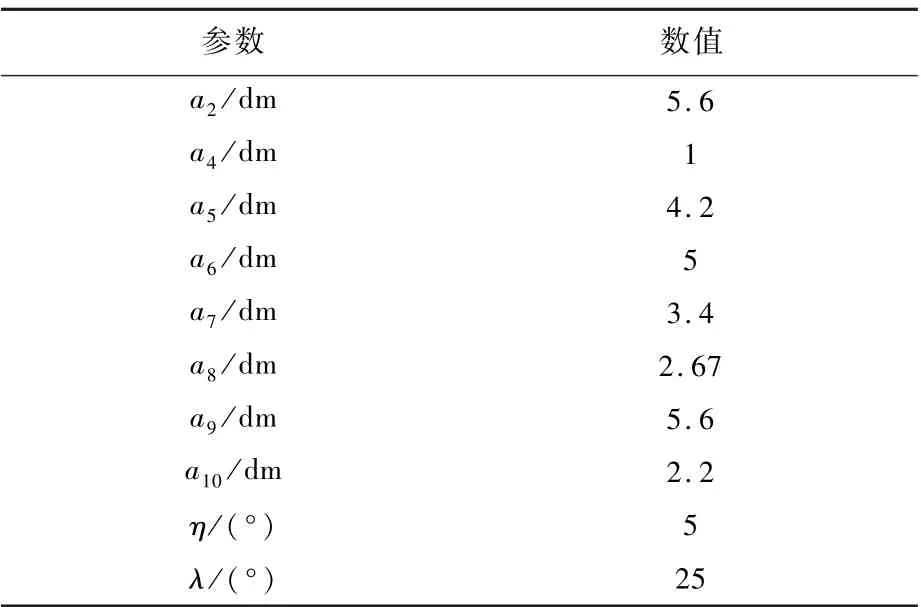
表10 图14 Stephenson 六杆机构杆长对应参数Table 10 Parameters of Stephenson six-bar linkage in Fig.10
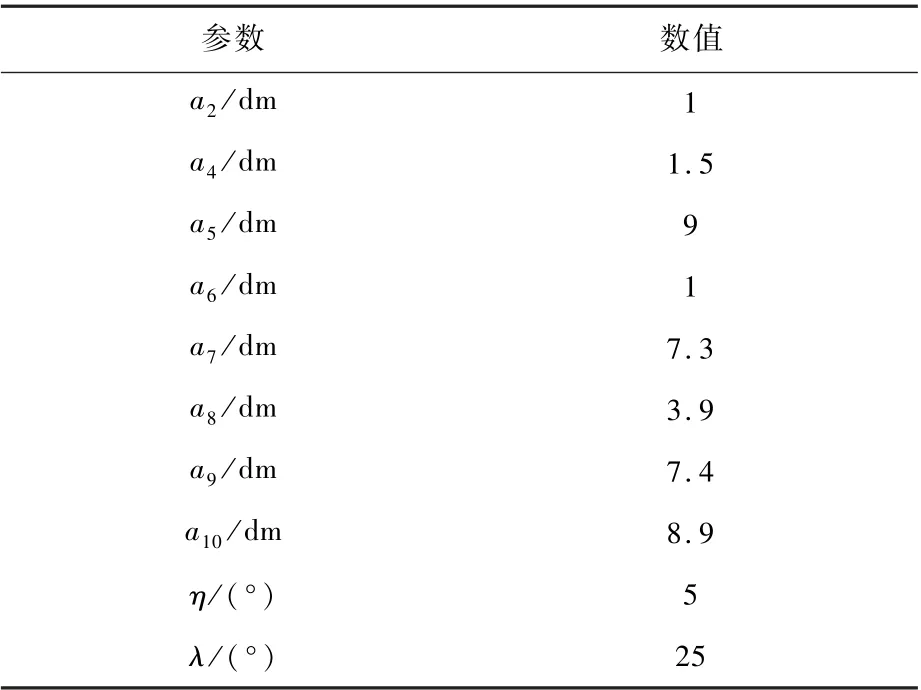
表11 图15 Stephenson 六杆输入θ5 曲柄对应参数Table 11 Parameters of Stephenson six-bar linkage with input joint θ5 in Fig.11
5 结 论
1) 依据连杆机构的分支识别图和杆间关系,通过所提出的曲柄分支图识别法,对几类典型平面4R、5R、仅含有转动副的Stephenson 六杆机构的曲柄判定分支识别图进行了绘制,并通过数据分析,得到了曲柄数目与位置,相比现行方法,可视化强,简单直观,便于理解。
2) 针对仅含转动副的复杂多环路连杆机构的曲柄问题,提出曲柄存在的2 条充分条件,并以Stephenson 六杆为例说明,证明方法对复杂多环路连杆机构的曲柄判定是有效的,弥补了现行方法的应用的不足。
3) 通过对比分析了曲柄分支图识别法与Grashof 定理、N 杆旋转定理的应用实例与应用范围,证明本文方法的适用范围更广,通用性更好。
4) 本文提出的曲柄分支图识别法具有可视化强、通用性佳等优点,可以为单闭环、复杂多环连杆机构的曲柄研究,提供一种研究思路,对含有复杂连杆机构的机械装备设计提供一定的理论指导。
