借助单位圆理解三角函数,发展数学核心素养
2024-06-18贾小宇刘春艳
贾小宇 刘春艳


摘 要:单位圆在三角函数内容中占有非常重要的地位. 从历史发展角度来看,由关注具体角的弦值转向任意角的三角函数,三角函数与圆的弧长、弦长的关系逐渐清晰化,三角学的发展也经历了算术、代数、几何、解析四个研究阶段;三角函数是周期运动代数化的代表,在微积分、几何等领域具有重要作用. 三角函数的产生与发展始终与圆有关,三角函数的基本性质,是圆的对称性的解析表现,教学中要充分发挥单位圆的作用. 借助单位圆,从模型角度理解三角函数概念的数学化过程,从几何直观上理解三角函数的性质和诱导公式,从整体上理解三角恒等变换与三角函数的关系.
关键词:三角函数;单位圆;几何直观
中图分类号:G633.6 文献标识码:A 文章编号:1673-8284(2024)03-0008-06
引用格式:贾小宇,刘春艳. 借助单位圆理解三角函数,发展数学核心素养[J]. 中国数学教育(高中版),2024(3):8-13.
三角函数是一类典型的周期函数,是高中数学函数主题的重要内容.《普通高中数学课程标准(2017年版2020年修订)》对于三角函数概念和性质的内容要求中提出:“借助单位圆理解三角函数(正弦、余弦、正切)的定义,能画出这些三角函数的图象,了解三角函数的周期性、单调性、奇偶性、最大(小)值. 借助单位圆的对称性,利用定义推导出诱导公式.” 教学提示中再次强调:“应发挥单位圆的作用,引导学生结合实际情境,借助单位圆的直观,探索三角函数的有关性质.” 虽然各版本教材对于此要求的具体呈现不同,但是单位圆在“三角函数”一章中始终处于非常重要的位置.
在三角函数的学习中,为什么要借助单位圆?如何借助单位圆?本文从历史发展和学科知识体系建构的角度梳理单位圆与三角函数的关系,并从学科教学的角度探讨如何发挥单位圆的作用.
一、从历史发展角度来看,三角函数的产生、发展与圆紧密联系
1. 从研究对象来看,由关注具体角的弦值转向任意角的三角函数
三角函数的起源与天文学联系紧密,而圆是天文学中常用的模型. 古希腊时期,天文学家描述天体运行理论,如同心球、周转圆或偏心圆模型均利用圆来刻画天体运行轨道. 这一时期的代表人物希帕霍斯(Hipparchus,约190BC—125BC)不仅利用周转圆和偏心圆模型解释了日月运动,还制作了弦表以完成许多精确测量. 例如,天体之间距离的计算依据天体运行轨道形状、天体相对地球位移对应的时长和角度. 因此,只需要考虑固定角的正弦值便可以完成天体距离的推演. 16世纪,哥白尼的学生印度数学家利提克斯(G.J.Rhaeticus,1514—1576)将正弦函数重新定义成直角三角形边长的比,从而使平面直角三角学从球面三角学中独立出来. 在这之后,锐角三角函数进入系统研究阶段. 直至三角学脱离天文学,数学从运动的研究中引出了一个基本概念,在之后的二百年里,这个概念在几乎所有工作中占中心位置,这就是函数——或变量间的关系——的概念. 正弦函数和余弦函数是一对源于圆周运动、密切配合的周期函数. 因此,锐角三角函数是通过研究三角形各种几何量之间的关系而发展起来的,任意角的三角函数是通过研究现实中的周期现象而发展起来的. 1748年,欧拉(Euler,1707—1783)在《无穷分析引论》中引入角的弧度制,使单位圆上用弧度制表示的角成为三角函数的自变量.
2. 从研究过程来看,三角函数与圆的弧长和弦长的关系逐渐清晰化
三角函数的概念经历了漫长的演化过程,也经历了与圆从合到分又到合的过程. 三角函数首次出现在希帕霍斯的弦表中,表示为在半径固定的圆中不同弧长对应的弦长值. 古印度人发展了希帕霍斯的思想. 阿耶波多(Aryabhata,约476—550)在《阿耶波多历数书》中给出一个类似的半弦表,说明了圆心角的一半与“半弦”的关系,取半弦(jya或jiva,印度梵文中“弓弦”的意思)定义正弦,现在我们使用正弦函数“sine”的词源正是“半弦”. 近十个世纪之后,利提克斯发现了圆心角与弧长的一一对应关系,突破传统正弦函数弧与弦的对应关系,将正弦改进为角的三角函数值. 至此,三角函数在经历了漫长的依托于圆而存在的时期后最终脱离了圆. 一个世纪之后,欧拉提出三角函数是对应的函数线与圆的半径的比值,从而使三角函数回归了圆. 例如,正弦函数的定义——单位圆上任意弧度角对应的正弦线,在弧度制意义下依然体现的是半弧与半弦的对应关系.
3. 从研究方法来看,三角学经历了算术、代数、几何、解析四个研究阶段
在三角学萌芽期,三角学用于报时、历法推算、航海、地理研究等人类实践活动. 它作为一种对天体运行路线和位置观察推算的方法,慢慢演化为球面三角学知识. 门内劳斯(Menelaus,约70—140)的《球面几何学》给出球面三角形的定义及相关基本概念,比较球面三角形与平面三角形的异同. 例如,球面几何学中的大圆相当于平面几何中的直线,小于半圆的大圆圆弧就是其两端点之间球面上所有路径中的最短路径. 又如,三角形是平面几何研究的核心问题,同样地,球面三角形的研究也是球面几何学研究的核心问题. 门内劳斯借鉴希帕霍斯的成果,用弦长表示球面三角形边长的关系,进行平面三角形定理在球面上的推广,首次使三角学脱离天文学. 另外,除了正弦和余弦的计算,阿拉伯学者引入正切和余切、正割和余割的概念,从算术和代数性质上发展了球面三角学体系. 在三角学确立期,三角函数定义在直角三角形中,目的在于解三角形和进行三角计算,体现在平面三角学的使用上. 在三角学成熟期,三角函数呈现真正意义上的函数解析性. 牛顿(Isaac Newton,1643—1727)和莱布尼茨(Gottfried Wilhelm Leibniz,1646—1716)给出三角函数的级数展开式. 约翰[?]伯努利(John Bernoulli,1667—1748)和托马斯·范泰德·拉尼(Thomas Fantet de Lagny,1660—1734)等给出三角函数的和差公式. 德国数学家迈尔(Frederic-Christian Mayer,1697—1729)在此基础上推导了解析三角的一般恒等式. 欧拉在《无穷分析引论》中对三角学进行了解析的叙述,从基本公式推导出全部公式,并发现了三角函数的周期性.
二、从学科知识体系来看,三角函数的地位和作用也与圆有关
1. 三角函数是周期运动代数化的代表
由于任意角的三角函数具有周期性,可以刻画具有周期变化规律的运动,在天文和物理中有大量应用. 例如,物理中的单摆是一种简谐振动,具有固定的频率、周期和振幅,可以由三角函数近似计算单摆运动的周期. 单摆的问题还密切联系着地球形状和万有引力定律的验证,同时推动着牛顿对二体问题和三体问题的研究. 又如,欧拉在将三角函数应用于天体运动的研究中,验证了牛顿在《自然哲学的数学原理》中提出的月球运动理论,从而引发了数学家们对三角级数的深入研究. 另外,1822年,傅里叶(Baron Jean Baptiste Joseph Fourier,1768—1830)在《热分析理论》中提出任何函数不论连续与否,均可以展开为一系列正弦函数. 这一思想为泛函分析、偏微分方程、计算数学等数学领域的发展提供了数学基础.
在物理领域,傅里叶级数被广泛应用. 自然界中的大多数运动或振动表现为周期运动的叠加,如可见光、琴的和弦等,它们都可以用形如[fx=a0+][n=1∞ancosnπxL+bnsinnπxL]的傅里叶级数来刻画,其中[L]表示周期.
由此可见,三角函数在自然科学和数学中的广泛应用使其成为反映现实世界运动的一种具有周期变化过程的重要函数,也使其成为周期运动代数化的代表.
2. 三角函数在微积分、几何等领域中的作用
三角函数是解析几何学和周期函数的分析学中最为基本和重要的函数.
在微积分中,三角函数与指数函数、对数函数这两个基本初等函数之间存在密切的联系. 例如,圆弧下的面积[a2-x2dx]和双曲线下的积分[x2-a2dx],两者相差一个符号,前者可以用三角函数表示,后者与对数函数有关,由此引发了三角函数与对数函数两者之间关系的研究,以及对复数的对数的讨论和欧拉公式特殊形式[eiπ=-1]的发现.
在解析几何和微分几何中,借助三角函数将笛卡儿坐标系转换为极坐标系,推动了平面、空间曲线和曲面的研究工作. 例如,欧拉在《无穷分析引论》中利用坐标变换将一般的三个变量的二次方程转化成标准型,得到六种曲面. 欧拉在《固体或刚体的运动理论》中,推导出通常所用的沿一条平面曲线运动的质点的加速度的径向和法向分量的极坐标公式.
在微分方程中,三角函数可以刻画特定微分方程的解,从而研究方程所反映的周期现象.
另外,常微分方程理论中的一个基本问题是解的性态,其中一个重要问题是确定微分方程是否存在周期解. 例如,Massera周期解定理,给出了一维非自制周期系统的周期解存在的条件,建立了解的有界性和周期性之间的联系.
借助李群和李代数的表示,也可以对微分方程进行对称性、稳定性、周期解等性质的分析. 例如,由微分关系式[xt+][xt=0]控制的简谐运动,通过定义新的坐标[yt=][xt],将这个二阶方程转化为由两个一阶方程构成的方程组[xy=01-10xy]. 我们可以借助矩阵[01-10]的指数函数得到方程组的一个通解,从而得出结论[xtyt]是[x0y0]的一个旋转. 由此可知,简谐运动系统的相空间轨道图是一系列圆心在原点的圆周. 其中,该通解中表示旋转的变换矩阵[costsint-sintcost]是李群SO(2)的群元,相应李代数元为[01-10],它们反映了相空间轨道的对称结构.
三、教学建议
基于前面的分析,我们得出如下结论.
一是三角函数产生与发展的过程始终与圆有关. 三角函数的定义是在研究圆的半径、半弦长、半弧长、弦长、弧长等量之间对应关系的基础上建立起来的. 之后,三角函数在微积分、微分几何、微分方程等数学领域中的应用也与圆紧密相连,即使是在球面三角学中,球面的“直线”就是圆,球面三角形由连接球面上三个顶点的大圆圆弧构成,球面三角函数研究的对象也与圆有关.
二是与其他基本初等函数相比,三角函数最重要的性质就是周期性,而圆周运动是最简单也最具代表性的周期运动模型. 三角函数逐步发展为反映现实世界中具有周期变化过程的重要函数,也成为周期运动现象代数化的代表.
三是三角函数与圆都具有很好的对称性. 对称在数学中非常重要. 圆是对称性最强的平面图形,大圆与小圆有相同的对称性. 正如毕达哥拉斯所言:“一切立体图形中最美的是球,一切平面图形中最美的是圆……正弦、余弦函数是一对用来描述单位圆的函数. 而圆的本质则在于其完美的对称性,即其旋转对称性和对于每一个直径的反射对称性. 所以正弦、余弦函数的基本性质,其实也就是圆的对称性的解析表现.”
另外,学生在初中阶段“图形与几何”领域已经系统地学习了圆的相关内容,了解了圆的对称性. 因此,在研究三角函数的概念、性质,以及诱导公式、三角恒等变换等内容的过程中,要充分发挥单位圆的模型作用,借助几何直观整体把握三角函数的内容,提升数学抽象、数学建模等素养.
1. 借助单位圆,从模型角度理解三角函数概念的数学化过程
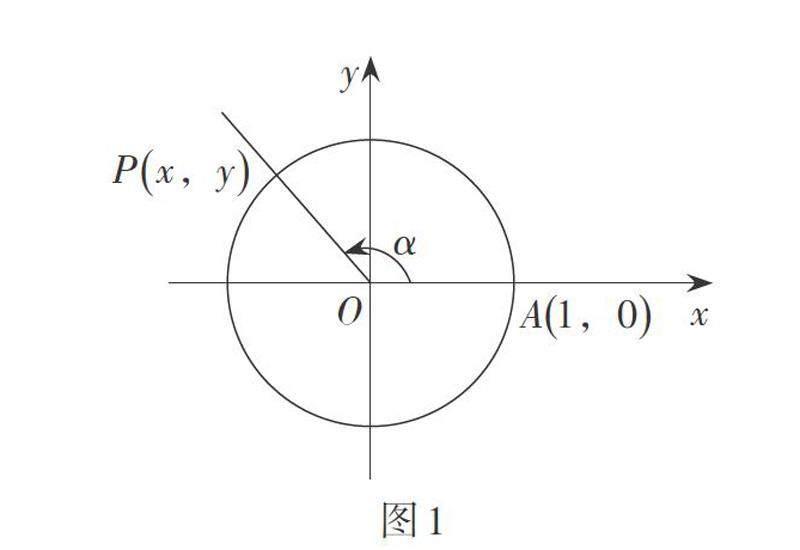
对于三角函数的定义,大体有两种方式:一种是直接借助单位圆,用角的终边与单位圆交点的坐标下定义,称为单位圆定义法;另一种是沿用锐角三角函数的定义方法,利用比值下定义,称为终边定义法. 两种方法本质上是一致的. 在实际教学中,常常从生活中的具体实例入手. 例如,摩天轮问题. 摩天轮匀速旋转过程中某位游客离地面的高度呈周期性变化,将实际问题抽象成单位圆上点P做匀速圆周运动,如何刻画点P的周期性呢?在实际问题中,学生感受到点P的位置随时间[t]的变化而变化,是关于时间[t]的函数. 当我们把单位圆放在平面直角坐标系中研究(如图1),自然会想到利用点P的坐标刻画点P的位置,但是选择哪个量作为自变量呢?时间[t]在单位圆的模型中是如何体现的呢?如何建立时间[t]与点P的坐标之间的关系呢?
前面学习其他函数时,具体实例中的自变量和对应关系是比较容易理解的. 例如,在研究指数函数时,典型的实例是碳14衰减,此问题以时间作为自变量,能明确写出两个变量之间的解析式. 而对于三角函数的概念,需要借助几何模型,以角作为自变量,建立点的坐标与角之间的对应关系,学生不具备相关的学习经验. 因此,对于三角函数的概念,如何选择自变量,以及如何构建变量之间的对应关系是教学的难点.
结合实际情境,借助单位圆,我们以时间[t]作为关键量,研究周期运动变化. 首先,当点P运动变化时,观察单位圆中哪些量也发生了变化. 当点P在单位圆上从点A开始运动时,点P旋转的角度与点P经过的弧、弦AP等都发生了变化. 其次,分析这些变量有什么变化规律,如何表示. 由于点P做匀速圆周运动,设角速度为[ω],随着时间[t]的变化,点P旋转的角度[α=ωt],点P经过的弧长l =[αr]. 特别地,在单位圆中,当[ω]为单位速度时,l =[α]= t. 此时,将问题归结为对点P的坐标与旋转角[α]之间对应关系的探索. 接下来,利用已有的研究函数的经验,借助几何模型(即单位圆),对于“几何元素之间的对应”给出三角函数的形式化定义.
为此,我们以时间[t]作为研究的切入点,通过分析在单位圆上的点的变化过程中相关量的变化规律,借助角速度和线速度的关系,构建旋转角和对应点坐标之间的对应关系,抽象出三角函数的概念. 通过上述数学化的过程,达成以下效果.
(1)帮助学生进一步理解函数是描述客观世界中变量关系和规律的最为基本的数学语言和工具. 在现实情境中,时间[t]是常见的变量,通过经历三角函数定义的数学化过程,进一步体会如何分析与建构其他变量与时间[t]之间的对应关系.
(2)帮助学生理解获得三角函数定义与其他基本初等函数定义的抽象过程的不同. 前面提到,指数函数的定义是通过对具体实例进行归纳、概括得到的,实例中两个变量之间具有明确的运算关系,而三角函数的定义主要是借助几何模型,通过分析几何元素之间的对应关系得到的.
(3)帮助学生进一步体会引入弧度制的必要性. 通过上述过程,让学生直观感受用弧度制来度量角,使得三角函数的研究明显简化.
(4)激活学生已有的认知基础,帮助他们进一步体会圆的作用,也为后续利用单位圆研究三角函数的其他内容作好铺垫.
2. 借助单位圆,从几何直观上理解三角函数的性质和诱导公式
性质是变化中的不变性和规律性. 相对指数函数和对数函数,三角函数的性质更加丰富,包括周期性、单调性、对称性、最值等. 三角函数是借助单位圆,利用几何要素之间的对应关系来定义的,而几何中圆的对称性是学生的认知基础. 因此,借助单位圆的直观,从运动变化的角度,利用数形结合,更能从整体上理解三角函数的性质.
例如,在平面直角坐标系xOy中,角[x]的顶点与原点重合,始边与[x]轴的非负半轴重合,终边与单位圆交于点P. 当角[x]的终边绕原点从[x]轴正半轴开始,按照逆时针方向旋转,观察运动变化过程,并思考以下问题.
(1)点P的坐标有什么变化规律?如何用代数符号表示?
(2)在角[x]的终边旋转一周的过程中,随着角[x]的变化,点P的坐标是如何变化的?利用(1)的结论,能否给出正弦函数、余弦函数的单调区间和最值?
(3)圆具有很好的对称性,原点O是圆的对称中心. 角x和角-x的终边与单位圆交点的坐标有什么关系?如何用代数符号表示?
(4)圆不仅是中心对称图形,也是轴对称图形,[y]轴是单位圆的对称轴. 在运动变化过程中,存在角[x]的终边关于[y]轴对称的两个位置. 此时,两个位置对应的角的大小有什么关系?分别对应的正弦值有什么关系?余弦值呢?如何用代数符号表示?
(5)[x]轴也是单位圆的对称轴,类比(4)的研究过程,能得到什么结论?如何用代数符号表示?
(6)直线[y=x]也是单位圆的对称轴,能得到什么结论?
(7)利用圆的对称性,还可以研究什么?
每个基本初等函数都具有独特的性质,三角函数是一类典型的周期函数,既具有单调性、奇偶性,又具有非常好的对称性. 借助单位圆,通过观察图形,分析运动变化中的不变性和规律,用符号语言表达,能够从直观上理解三角函数性质和诱导公式的本源,体会数形结合方法的作用.
3. 借助单位圆,从整体上理解三角恒等变换与三角函数的关系
三角恒等变换是对三角函数式进行恒等变形. 很多学生感觉此内容距离三角函数的概念与性质比较远,相对独立,又因为公式多记不住,感觉难. 对于公式的理解,同样可以发挥单位圆的作用,帮助学生建立三角恒等变换与三角函数的概念、性质之间的联系,体现三角函数研究内容和研究方法的一致性.
借助单位圆的中心对称性,关于x轴、y轴、直线y = x的轴对称得到诱导公式. 对于圆的任意一条对称轴,可以得到什么结论?不妨以任意角[α]的终边所在的直线[l]为对称轴,在单位圆上任意取一点P. 设点P关于直线[l]的对称点为点[P′],角[α]的终边交单位圆于点A. 连接[PP′],交直线[l]于点B. 当点B在角[α]的终边OA上时,如图2所示;当点B在角[α]的终边OA的反向延长线上时,如图3所示. 如图2,设[∠AOP]=[β],利用三角函数的定义和对称性,得到点[Acosα,sinα],点[Pcosα+β,sinα+β],点[P′cosα-β,sinα-β],点B[cosα+β+cosα-β2, sinα+β+sinα-β2]. 因为[OB=OP ? cosβ=cosβ],由三角函数的定义得到点[Bcosβcosα,cosβsinα],所以[cosα+β+cosα-β2=][cosαcosβ],[sinα+β+sinα-β2=sinαcosβ]. 变形即可以得到和差化积公式和积化和差公式.
另外,圆还具有旋转对称性. 以单位圆的圆心为顶点、x轴的非负半轴为始边画出角[α,β,α-β],根据三角函数的定义写出这三个角的终边与单位圆交点的坐标,然后利用圆的旋转对称性建立等量关系,再利用两点间的距离公式得到两角差的余弦公式. 这样,以单位圆的几何直观为纽带,将三角恒等变换与整个三角函数内容融为了一体.
参考文献:
[1]项武义,张海潮,姚珩. 千古之谜与几何天文物理两千年:纪念开普勒《新天文学》问世四百周年[M]. 北京:高等教育出版社,2010.
[2]克莱因 M. 古今数学思想:第一册[M]. 张理京,张锦炎,江泽涵,等译. 上海:上海科学技术出版社,2014.
[3]克莱因 M. 古今数学思想:第二册[M]. 石生明,万伟勋,孙树本,等译. 上海:上海科学技术出版社,2014.
[4]克莱因 M. 古今数学思想:第三册[M]. 邓东皋,张恭庆,译. 上海:上海科学技术出版社,2014.
[5]章建跃. 为什么用单位圆上点的坐标定义任意角的三角函数[J]. 数学通报,2007,46(1):15-18.
[6]项武义. 基础几何学[M]. 北京:人民教育出版社,2004.
[7]梁宗巨. 世界数学通史:上册[M]. 沈阳:辽宁教育出版社,1995.
[8]VERDUN A. Leonhard Eulers early lunar theories 1725-1752[J]. Archive For History Of Exact Sciences,2013,67(5):477-551.
[9]MASSERA J L. The existence of periodic solutions of systems of differential equations[J]. Duke Mathematical Journal,1950,17(4):457-475.
[10]MIWA T,JIMBO M,DATE E. Solitons:Differential equations,symmetries and infinite dimensional algebras[M]. Cambridge:Cambridge University Press,1999.
[11]休森. 数学桥:对高等数学的一次观赏之旅[M]. 邹建成,杨志辉,刘喜波,等译. 上海:上海科技教育出版社,2022.
[12]顾沛. 对称与群[M]. 北京:高等教育出版社,2011.
[13]项武义. 基础分析学之一:单元微积分学[M]. 北京:人民教育出版社,2004.
