几何直观，不只是直观

薛正桧

[摘 要]目前的几何直观教学存在很多误区，严重影响了学生的学习。教师可从“只注重直观、只注重结果、只注重理解”等三个方面入手，就几何直观教学误区进行分析，改进教学策略，从而提高课堂效率。

[关键词]小学数学 几何直观 认识误区 抽象提升

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2016）35-048

借助几何直观可以把抽象复杂的数学问题变得简明、形象，有助于探索解决问题的思路。当学生遇到复杂难懂的问题时，教师可以鼓励他们动手画出直观的几何图形，借助图形的特征和规律，找到解决问题的方案。但在实际教学中，部分教师做法不当，使得效果大打折扣。

一、只有直观分析，没有抽象提升

许多教师潜意识里认为只要有了直观的手段，有了图形的参与，学习的效率就能提高。却不曾想，只进行直观教学，不进行适当的抽象与提升，导致几何直观只有形式没有内涵，适得其反，反而影响了学生抽象思维的形成。

例如，教学“乘法的运算律”时，对于“某商场短袖衫32元一件，裤子45元一条，夹克衫65元一件，现在要买5件夹克衫和5条裤子一共需要多少钱？”这道题，多数教师采取的是几何直观教学手段，鼓励学生用“□”表示夹克衫，用“○”表示裤子，画出如下的示意图：

画出示意图后，学生快速列出算式45×5+65×5，并用两种方法解出问题的答案。事实上，学生并没有理解乘法分配律的实质，只是知晓了解决应用题的两种方法，教学漏洞显而易见。为此，教师在学生画出直观图的基础上，可这样进行教学：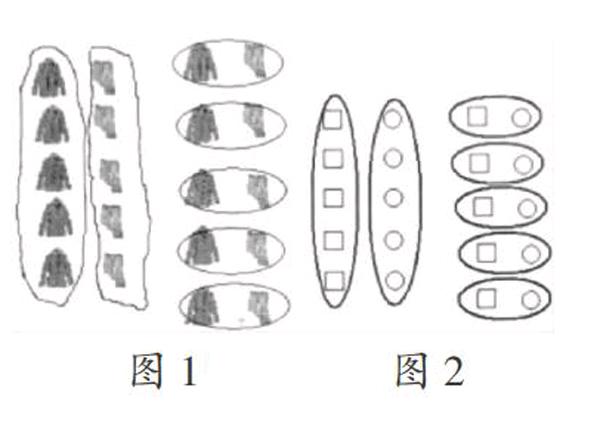

首先，教师要使学生明确第一种方法是先分别求出求夹克衫的钱数和裤子的钱数，再把它们加起来，第二种方法则是把夹克衫与裤子看成一个整体去计算。其次，教师还应鼓励学生多练习变式题，如“买3件夹克衫和3件短袖衫一共需要多少钱？也可以有两种解答方法吗？如果买3件夹克衫和5件短袖衫呢？”。最后，教师应对乘法分配律进行细致的讲解，鼓励他们进一步思考，以同步发展和提升他们的抽象思维。

二、只重结果呈现，忽视过程优化

几何直观是一个结果，也是一个过程。小学生正处于人生发展的初级阶段，知识储备有限，思维方式也不完善。教师既要使学生学会利用图形来描述和分析问题，又要使之学会利用图形描述和分析问题。

例如，教学“分数的加减法”时，有如下题目：一块长方形的试验田，其中黄瓜种了1/2，番茄种了2/4，求黄瓜与番茄一共占这块地的几分之几。教师在教学的过程中通常是让学生先根据题意列出算式，然后进行折纸和涂色，从而使学生明白1/2等于2/4，进而理解通分的概念，知晓应把异分母分数化为同分母分数进行计算。

教师还应进一步思考：“画图时的一些注意事项每一位学生都清楚吗？他们真的把异分母分数加减与整数加减和小数加减等建立了联系吗？异分母分数加减 “单位统一”与“转化”这两个基本要素是学生自主发现的吗？”教师要让学生通过画图明确图形的单位1的大小必须相同，通过交流明白画图的方法可以各不相同，但最终都指向一个统一的算理（如下图）。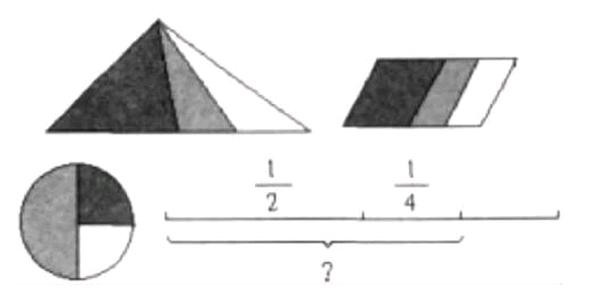

在小学数学中，题型较多，几何直观可采取的画图方式也是多种多样的。教师在教学的过程中应该重视培养学生的思维能力，重视发展学生的创新能力，当学生有不同方法时，教师应和全体学生一起探究该方法是否正确，与其他方法比较，哪个方法更优越。

三、只重表层理解，忽视实践体验

小学生由于年龄较小，性格上活泼好动，注意力难以集中。教师在进行几何直观教学时可充分利用这一点，调动学生动手实践的积极性。

例如，教学“有一群小动物组织去看电影，它们站成了一排，从左边开始数的话，小兔子站在第六个位置上，而从右往左数的话，小兔子站在第四个位置上，一共有多少个小动物去看电影呢？”这道题时，教师鼓励学生先根据题意画出示意图，再进行求解。但对于低年级学生而言，即使画出了示意图，理解题意仍是比较困难的事情。对此，教师可选出几位学生站到讲台前，根据题目意思进行游戏模拟。通过亲身参与，亲身感受，学生的感悟变得直观、深刻，从而准确把握题意。

几何直观不只局限于画图，它还可以是角色扮演。角色扮演这种实践体验能让学生获得真实的感受，从而真正理解题意，解决问题，掌握知识。

综上所述，几何直观不只是直观，它既有结果也有过程，教师只有认识到它的本质，才能让它真正服务于教学，才能更大限度地发展学生的数学思维能力。

（责编 吴美玲）