基于“慢学习”理念的初中数学教学研究

李璠琼

［摘  要］ “慢学习”即体验式、思考式学习. 学生在“慢节奏”的学习过程中，能不断提高自身的认知与领悟能力. 文章从“慢学习”的理论基础出发，认为“慢学习”理念最突出的是“以生为本”的教育价值，主要表现在“尊重学生的差异性”“突出学生的主体性”以及“关注学生的学习体验”等方面，并从“择取合适路径”与“确立有效方式”两方面具体谈谈“慢学习”的实施措施.

［关键词］ 初中数学；慢学习；慢教育；认知；后延

“慢学习”属于“慢教育”的一个分支，是指体验式、细致化或思考式学习，它是在学生独立思考、自主分析的基础上逐渐领悟、参透知识内涵的过程. “慢学习”需要给学生提供充足的“思考”与“领悟”时间，知识随着润物细无声的“慢加工”在学生思维上形成一定的突破，成为后续“快攻”问题的利器［1］. 从本质上来说，“慢学习”就是放慢学习节奏，让思维、眼界跟上学习进度，为厚积薄发夯实基础.

理论基础

张文质先生认为教育是生命潜移默化的过程，这种变化是细微、缓慢的，需要经历生命的沉淀. 他的“慢教育”理念与讲究“时效性”的教学理念形成了鲜明对比. 王卿文教授曾经提出：数学教学不能片面地追求速度，还要经历“慢”的过程，只有经历反复思考，才能达到深刻理解、领悟的目的，从真正意义上获取数学的真谛与精髓.

实践证明，数学学习有一定的诀窍，想要达到精深的目的，就不能图“大量”“快速”，“少而精”能让学习变得扎实与牢固. 正如美国心理学家迪安·德尔·赛思托所言：人类需要用一种慢且深的思维方式，应付节奏越来越快的学习. “慢学习”理念隨着“慢教育”思想的盛行而浮出水面.

“慢学习”突出“以生为本”的

教育价值

1. 尊重学生的差异性

世界上没有两片完全一样的树叶，也没有思想完全一样的学生. 每一个学生都是独立的个体，在学习习惯、方式方法与思维意志等方面有着显著的差异性. 因此，即使同一个教师讲授同样的内容，在学生那里却会出现不一样的学习状态——一些思维敏捷、反应迅速的学生能快速掌握所学内容；而一些基础薄弱、反应迟缓的学生却需要一个缓冲的过程.

“慢学习”是在“慢教育”理念基础上衍生而来的学习方式，是基于实际学情的一种课堂关怀，是在充分尊重并理解学生的基础上，让学生对学习进行充分思考、理解与体验的过程［2］. 尤其对于一些教学重难点，教师组织学生慢学、细学，让学生学精学透，达到理解知识本质、领悟知识精髓的目的. 从学生实际情况出发，实施“慢而细，细而深”的教学策略，体现新课改背景下的“生本”状态.

2. 突出学生的主体性

新课标明确提出学生是课堂的主人，数学课堂除了讲授知识与技能外，更重要的是培养学生主动思考、自主探究与合作交流. 这就需要教师为学生提供良好的学习平台，让学生充分展示课堂中的主体性地位. “慢学习”模式让学生拥有充足的时间思考、体验、感知知识形成与发展的过程，尤其遇到较难的知识点时，更需要在“慢学习”状态下进行思辨、体悟.

例如学生解题时出现了错误，教师可鼓励学生通过自主分析探寻错误根源，辨析错误类型，并在与同伴交流与共享中突破自我、提升自我，避免类似问题的再次发生. “慢学习”最忌讳教师在前面“牵着走”，当然更不能是教师在后面“赶着走”，而应该营造一种师生共同学习的情形，凸显出学生在课堂中的主体性地位.

3. 关注学生的学习体验

正因为“慢”，学生才有充足的时间体验；正因为“慢”，学生才有充足的时间专注；也正因为“慢”，学生才拥有充足的时间研机析理、深学透悟. “慢学习”就是通过对学生思考过程的延长，让学生在“慢”中充分感知数学学科的“活”，体验数学思想的博大精深. 真正意义上的“慢学习”是慢而不怠，虽然速度慢，但走心.

一般情况下，“慢学习”带来的学习体验是一个循序渐进的过程：①初始阶段，通过模仿单一的知识点，初步体验知识的产生并能用简单的知识解决单一的问题；②尝试阶段，该阶段以“同伴互助”的方式为主，学生通过观察与分析进行知识的关联与思路的建构；③合作阶段，即通过合作交流的形式进一步理解知识，并尝试将新知纳入原有的认知结构中；④自主探究阶段，通过“慢”探究，揭露知识本质，完善认知结构.

“慢学习”的实施措施

1. 择取合适路径

“慢学习”的目的在于让学生拥有充足的时间更好地消化、吸收所学知识，培养与发展学生的“四基”与“四能”. 教师设计教学任务时，可结合学生学情与教学内容的特点为学生留下充足的思考与探索的时间和空间，充分体现“以学为中心”的教学理念.

注重审题译题，往往能培养学生的联想能力. 数学本就是一门抽象学科，尤其在中学阶段，涉及的知识点较多，一些关键词语之间缺乏明显的联系性，这就需要教师引导学生学会通过联想分析问题，以探寻各个知识点之间存在的关联信息. 如图形类问题，就需要从题意、解决思路等角度出发进行“慢探究”.

问题：（1）点P位于直线y=x－2上吗？

（2）已知点A（3，0），B（0，6），点P在△ABO的内部运动，m的取值范围是什么？

问题（1）比较简单，学生很快就能自主得到正确答案（略）. 对于问题（2），不少学生紧扣“点P在△ABO的内部运动”这个条件，获得0＜m+1＜3和0＜m－1＜6，解出1＜m＜2这个结论.

如此获解，一不小心就掉进了思维误区. 究其原因，主要在于学生审题时，忽视了问题（1）的存在，对两个问题之间的联系视而不见. 其实，解决问题（2）只需要从以下两方面入手即可：①点P在△ABO的内部运动；②点P在直线y=x－2上运动.

放慢审题译题的脚步，看似耗费了一定的解题时间，却是避免浪费解题时间的根本. 学生一旦明确了问题中所有条件与结论的深意，就能“以不变应万变”、通过联想顺利解题. 有些学生为了快速解题，常常囫囵吞枣地将题设条件扫视一遍，提笔就写，一写就错. 其实，审题译题“慢”，往往能成就解题“快与准”.

2. 确立有效方式

数学知识并不是独立存在的个体，不同知识的学习与不同能力的培养具有不同方法：①溯源法，通过对问题的表象与属性进行归纳总结，抽象出概念要义；②内化法，应用所学知识，理解知识内涵与本质，并将所学知识转化为技能；③后延法，通过探究或拓展等方式提升思维能力，建构新的解题策略.

（1）追根溯源，灵活思维.

每一个概念、定理、法则或公式等都是历史的积淀，都是前人走过漫长的路总结提炼而来的. 若将这些现成的结论直接展示给学生，学生只是走前人走过的路，只能机械式记忆知识，谈不上理解与灵活应用. 只有带领学生亲历定理、公式或法则形成的过程，学生才能走自己的路，形成自己独特的见解，在应用时才能得心应手.

如勾股定理在数学学科乃至其他学科领域中占有重要地位，若教师直接将勾股定理呈现给学生，学生只能单纯地记住这个定理，对这个定理缺乏情感；若教师带领学生从数学文化的角度出发，与学生一起感叹我国西周的数学家商高的重大发现“勾三股四弦五”，与学生一起浏览古希腊的毕达哥拉斯的证明过程，与学生一起查阅古往今来数百种勾股定理的证明方法. 当学生经历这一切后，对勾股定理会产生不一样的情感.

此时再证明勾股定理，便能有效激发学生的探索欲. 将数学史作为铺垫证明定理，学生展现出“慢”且“深”的探索过程，应用拼图法、等积法、割补法、搭桥法等，有效训练学生的思维能力与探索精神.

（2）同化顺应，内化吸收.

新课改背景下的数学教学是“能力立意”的教学，要将知识转化为能力，少不了内化过程. 从认知心理学来说，知识内化存在“同化”与“顺应”两个环节. 同化是指将知识吸纳到原有认知结构的过程；顺应是主体改变自己认知结构，建构新的认知体系的过程［3］. 想要从真正意义上消化、吸收所学知识，这两个环节缺一不可.

例2？摇 问题1：若想用一根40 m的绳子围一个长方形，所围成的长方形的长是不是宽的函数？长方形的面积是长的函数吗？

问题2：沙漏是我国古代的一种计量时间的仪器，它根据容器上部分的细沙漏到下部分的数量计量时间. 在这个过程中，谁为自变量？谁是谁的函数？

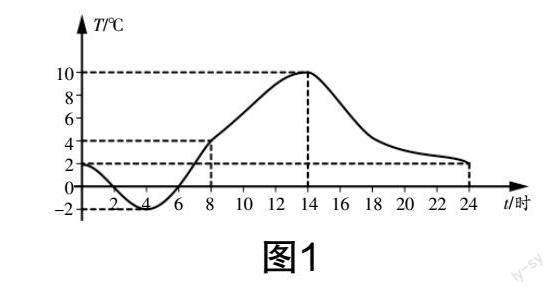
问题3：如图1所示，这是一张表示时间与气温之间关系的图象，请根据图象判别以下两个说法是否正确.①时间为温度的函数；②温度为时间的函数.

此例为“函数”部分的内容. 前面两问（问题1和问题2），学生通过对知识的“同化”，可对新知建构一种认同感，此为知识正强化不可或缺的环节；问题3为辨析题，让学生通过自我争辩对函数概念中的核心词“唯一”有新的理解，深化学生对函数这部分内容的认识.

若教师直接呈现问题3，则学生对函数的认识会因为缺乏同化过程，难以准确判断究竟时间是温度的函数，还是温度是时间的函数. 知识的理解本就要遵循由浅入深、循序渐进的过程，教师利用起点低、跨度小、密度大的问题串引导学生思考，虽然教学进度“慢”了一些，但学生不仅能内化吸收知识，还能获得探索问题的能力，从真正意义上践行以“能力立意”为目标的教学理念.

（3）适当后延，感悟提升.

为了促进学生深刻理解知识，对数学思想方法有所品悟，教师可为学生适当地提供问题探究活动. 引导学生在对问题进行深入探究的过程中获得新的体验与感知，并从中提取解决问题的一般方法与数学思想，为核心素养的发展奠定基础.

例3  已知在平面直角坐标系中，点A（－1，4），B（4，9）.

问题：（1）利用尺规作图法，到y轴上寻找点M，使∠AMB为直角.

（2）设点P（N，0）满足∠APB=45°，则n的值是多少？

（3）y轴上是否存在一点Q可使∠AQB=135°与AQ=BQ同时成立？若存在，求出点Q的位置；若不存在，说明理由.

问题（1）可通过辅助圆的添加，结合直径所对的圆周角为直角这个定理作图探点；问题（2）从问题（1）得到启示，画出以AB为弦，∠APB为周角的圆和x轴相交，结论一目了然；问题（3）可以先假设点Q满足条件∠AQB=135°或AQ=BQ中的一个，然后探索是否满足另一个条件即可.

此题组训练不仅夯实了学生对“圆的内接四边形性质”的理解，还培养了学生的数学发现能力、数学演绎能力、数学建模能力，建构“探索—发现—演绎—建模”的解题策略，为后续解决更多的复杂问题提供了研究方法上的帮助.

知识后延虽然放慢了学习进度，却帮助学生积累了研究经验，让学生掌握了解决这一类问题的技能. 因此，“慢学习”是实现“触类旁通”的最佳途径. 学生正因为拥有充足的自主支配时间，才形成了积极思考与主动学习的习惯；正因为有了充足的思考时间，才有了更多的解题经验，体验到解题成败的酸甜苦辣，并在不断改进与拓展中完善认知结构，提高解题能力.

正所谓“有自由时间，才有自由思想”. 新课改背景下的数学教育教学应致力于引发学生自主思考，让学生的思维处于不断生长的状态. 课堂因有思考而变得灵动，思维因有生长而充满生机.

总之，“慢学习”的路很长，其学习成效取决于学生在课堂中的地位以及教师是否有充足的耐心去理解数学、理解学生、理解教学，是否能够以爱育人. 只要教师潜心研究，静心等待，一定能讓“慢学习”结出丰硕的果实.

参考文献：

［1］陈柏良. 慢下来才会有“风景”［J］. 中学数学教学参考，2015（19）：23-25.

［2］林风. 数学教学要讲究“慢”教学［J］. 中国数学教育，2012（22）：5-8.

［3］杨翠蓉，周成军. 布鲁纳的“认知发现说”与建构主义学习理论的比较研究［J］. 苏州教育学院学报，2004（02）：27-31.