几何画板优化复习教学的措施研究

唐浩达

[摘 要] 利用几何画板进行专题复习教学，一方面可拓宽学生的视野，提高学生的“四基”与“四能”；另一方面可提升学生的数学思维，提高复习成效.文章从几何画板教学的优势出发，以“二次函数图象”的专题复习教学为例，具体谈谈如何用几何画板优化数学专题复习教学.

[关键词]二次函数图象；专题复习；几何画板

初三数学专题复习课程一般安排在二轮复习中，这是基于学生经历了一轮复习后，已经梳理完知识体系，需要从更高层次上审视知识的整合与应用.专题复习是加强知识应用交叉渗透的过程，意在从整体性、融合性、创造性与应用性等方面提升学生的数学能力.借助几何画板进行专题复习，不仅能将几何画板在教学中的优势展现出来，还能从真正意义上提高专题复习的成效.

几何画板的优势

1.直观展示变量关系

与传统教学模式相比，几何画板更具直观性，它可将抽象的变量或数量关系直观形象地展示出来，将一个量的变化引起另一个量变化的动态效果演示出来，如函数关系，就可借助几何画板将因变量与自变量间存在的关系进行演示[1].从某种意义上来说，几何画板打破了传统割裂知识联系的现象，为数学研究开辟了一条新的道路.

2.凸显知识形成过程

几何画板的操作技术比较简单，每一个学生都能自主操作与应用几何画板，因此它为学生自主参与学习营造了较好的学习氛围与环境.传统教学对概念的分析一般只能从文字上去完成，而几何画板却能完整地展示概念的形成过程，尤其是对一些数量关系的分析，让学生的学习实现由表及里、化繁为简，学生在几何画板的辅助下能从宏观的视角掌握数量所蕴含的规律.

3.简化问题难度

几何画板可将一些学生难以理解的内容变得直观化，让学生能快速理解问题的本质，为解题奠定基础.同时，它还可通过一些简约的操作来动态演示一些抽象的问题，以提高学生的思辨能力与操作能力.教师若将几何画板应用到数学专题复习教学中，能有效降低问题难度，提升教学成效.

教学过程

1.教学分析，明确目标

教学分析包含了学情分析、教学内容分析与几何画板技术功能分析三个部分的内容.从学情与教学内容特点来看，中考二轮复习阶段，学生对基础知识已经掌握得比较扎实.由于本节课是“二次函数图象”的专题复习课，因此可在学生原有认知基础上设计教学活动，以纵深深化学生对二次函数图象问题的认识；从技术功能的角度分析，几何画板的动态演示功能，可将二次函数图象直观地展示在学生面前，降低问题难度，让学生能更客观、快速地理解问题.

教学目标的确定主要是通过思维导图与游戏诊断等方式来进行，教师可要求学生在课前分组进行思维导图的绘制，同时对本节课的教学内容进行整理，择取优秀作品投影展示.学生通过自主探索与合作交流来进一步厘清知识脉络，为专题复习奠定知识基础.同时，教师还可通过小游戏的创设引发学生互动，以诊断学情，为制订教学目标服务.

2.设计问题，实施教学

二次函数章节主要涉及数形结合思想、函数思想、转化与化归思想等.为了提高专题复习的效果，教师可从渗透数学思想方法的角度出发，结合学情设计一系列问题，组成问题串，以启发学生的思维.借助几何画板进行问题的设计与思想方法的渗透，能让学生在动态展示的图形中感知合情与演绎推理的过程，以促进学生更好地总结与归纳基本模型，提炼各种数学思想方法.

为了彰显几何画板在此环节中的作用，笔者特别精选例题，并配以相应的变式题来启发学生的思维，引发学生自主思考与探索.

问题 分析二次函数y=m（x2-6x+8）（m>0，且为常数）的图象特点.

生1：因为二次项系数m>0，所以该函数图象是开口向上的抛物线.

生2：因式分解x2-6x+8这一部分，得y=m（x-2）（x-4），即y=0时，x=2或4.由此可明确二次函数y= m（x2-6x+8）的图象与x轴的交点为（2，0），（4，0）.

師：根据以上两位同学的结论，是否还有其他新的发现？

生3：根据二次函数y=m（x2-6x+8）的图象与x轴的交点，可知x=3为y=m（x2-6x+8）的对称轴.

师：很好！接下来大家一起观察用几何画板绘制该二次函数图象的过程.

第一步，如图1，作一条直线l，令其与y轴成平行关系；第二步，在x轴的上方，直线l上任取点M；第三步，获取点M位于直角坐标系上的纵坐标“m”；第四步，借助m的值作出函数y=m（x2-6x+8）的图象，所作图象与x轴相交于点A，B，与y轴相交于点C；第五步，拖动点M，观察该图象的变化情况，直观感知函数y=m（x2-6x+8）图象在运动时恒过点A，B.

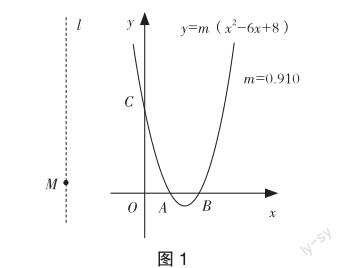
变式题1 如图2，以AC为对称轴，把原点O反射至点O，此时点O与O关于直线AC对称，拖动几何画板上的点M，点O能不能落在线段BC上呢？

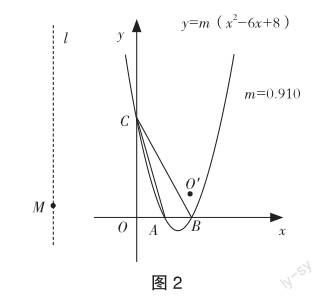
学生自主操作，其中一位学生提出：当拖动点M时，点O虽然可以移动，不知道为什么却一直无法落在线段BC上.另一位学生也提出：结合题中条件，可知AC平分∠OCB，则点A到BC与OC的距离相等，且必然都等于2，而AB的值也是2，这就出现了矛盾.由此能判断，不论如何移动点M，点O必然无法落在线段BC上.

笔者肯定了以上两位学生的说法，并引导学生继续调整点M的位置，并提出新的问题.

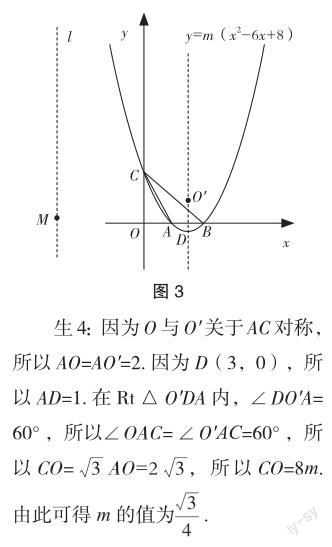
变式题2 借助几何画板进行操作演示，如图3，依然以AC为对称轴，将原点O反射至点O，作二次函数y=m（x2-6x+8）图象的对称轴，令其与x轴相交于点D，拖动点M，当点O恰巧位于图象的对称轴上时，M的值是多少？

变式题3 继续观察几何画板，如图4，在二次函数y=m（x2-6x+8）图象的对称轴上任取一点P，连接AP，CP后拖动点P，测得∠APC为一个钝角，上下拖动点P，发现∠APC的度数随着拖动而变小，在某个时刻会成为直角，且向上或向下都有出现直角的机会.以同样的方法拖动点M，却发现∠APC即使在最大的时候，都无法成为直角.由此可以看出∠APC与m有一定的联系，当m满足什么条件时，∠APC存在两次成为直角的机会？

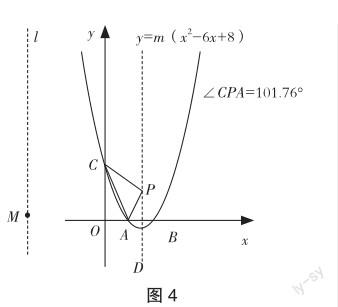
学生沉思，有一位学生犹豫地提出“是否可以作以AC为直径的圆来解决这个问题？”笔者鼓励学生自主尝试.该生作图分析，并在笔者的点拨下，继续应用几何画板加以探索：如图5，拖动点M，发现圆Q与图象的对称轴相切.

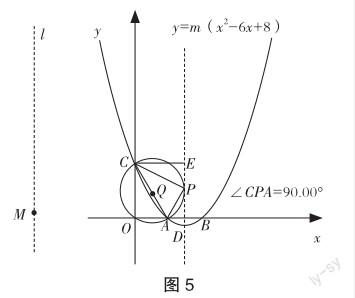
3.總结提炼，巩固升华

要求学生对本节课所探索的知识要点、几何画板的应用方法、学习感受等进行梳理与总结，并应用几何画板将所有内容罗列到一幅思维导图中，以构建完整的知识框架，形成结构化的认知体系，为后续学习夯牢根基.

几点思考

1.几何画板是提高专题复习效率的利器

专题复习强化学生对某个知识点或某类题的灵活应用程度，让学生获得用某种数学思想方法或某个知识版块的内容来解决一类问题的综合能力，并在例题与变式的应用中不断提升熟练程度，达到以一通百的目的[2]。

本节课教学的重点和难点在于函数图象的几何性质的探索中.几何画板的介入，不仅精确地将每一幅图展示出来，还将图中动点的变化过程直观地呈现给学生，让学生在图形的动态变化中感知几何图形的稳定性，学会透过现象看本质，以发现图形演变背后恒定不变的规律.

纵观本节课的教学，所有的问题都紧紧围绕原问中所提到的二次函数而展开，该二次函数图象为一条随m值变化而变化的抛物线，若想让学生直观地感知这条抛物线，最便利、高效的方法就是借助几何画板进行演示.这种设计方法不仅激活了学生的思维，帮助学生提炼了数学思想，还从真正意义上提高了教学实效.

2.几何画板应用于复习课可降低思维起点

数学是思维的体操.不论什么课型的教学，都要关注学生原有的思维水平，尽可能创设每一个学生都能积极参与理解的问题，以激活学生的思维，让学生的思维沿着由浅入深的问题螺旋式上升.几何画板的介入，可有效降低复习课的起点，让学生更积极地参与到问题的探究中去.

笔者本来创设的变式题1是：线段AC能否平分∠BCO，若能，求m的值；若不能，说明理由.这个问题在另一个班应用后发现，学生对此问的思维很不活跃.为了进一步提高教学实效，笔者与备课组其他成员一起研讨，经分析，认为借助几何画板的动态演示功能将原点O沿着AC进行反射，求反射点是否落在线段BC上更能激发学生的思维.这种处理方式，不仅增加了学生的思维与逻辑容量，还给学生制造了动手操作几何画板的机会，增加学习兴趣的同时提高了复习成效.

反观变式题3，点P，M的拖动以及∠APC的度数的测量，直观演示了点P运动时，∠APC能否成为直角，受点M位置的影响，也就是受m的值的影响.由此可见，几何画板的介入成功降低了学生审题与解题的难度，这是降低思维起点的重要举措，也是让每一个学生都能积极参与课堂教学的关键.

3.几何画板可跳出多媒体课件的局限

课件是教师根据教学目标与教学需求设计的教学活动方案，课件设计的目的是优化教学系统决策过程，它体现了教师作为课堂主导的事前工作.在传统教学中，不少教师将课件作为直接“播放”的利器，这部分教师将课堂可能发生的情况都做好了预设与化解方案，而事实上，课堂教学是一个不断变化的动态过程，不管多么优秀的教师都无法预见实际教学中的每一种情况，这也是课件的局限性所在.

几何画板的介入成功突破了课件的这种局限性，它的易操作性能让教师在课堂上实时完善课件，应对每一种突发情况，让课堂在操作中动态生成.其实，学生观看教师操作几何画板或自主操作几何画板的过程，也能进一步了解知识的来龙去脉，这对帮助学生更好地理解数学原理、知识内涵以及发展数学核心素养具有重要意义.

参考文献：

[1] 冯伟，张骅.几何画板在初三专题复习课中的应用——以“二次函数图象”为例[J].中学数学月刊，2021（1）

[2] 朱炎林.初中数学二轮复习的选题方法和教学策略[J].数学教学通讯，2018（4）.