初中数学解题中数形结合的应用

汪振宇

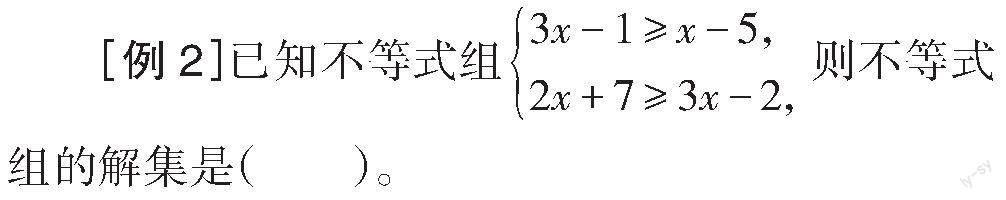
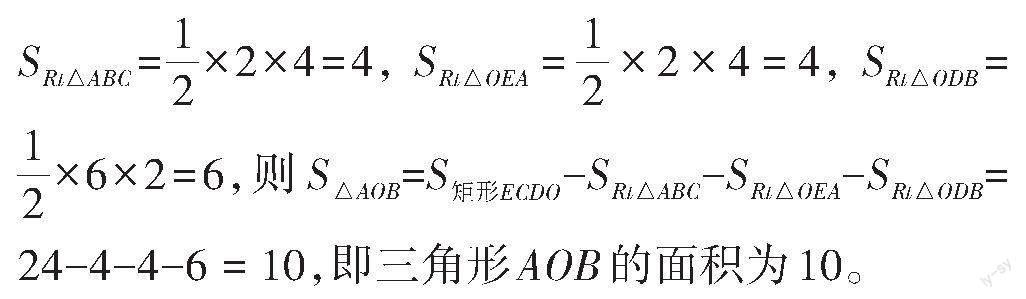
［摘 要］初中数学主要研究数量关系和图形关系，极具逻辑性和抽象性，学生在学习过程中通常会遇到不少困难，尤其是在解题环节更是深受困扰。在初中数学解题训练中，为处理一些难题，教师可指导学生应用数形结合思想，让他们学会通过数形结合的方式解答问题。文章对初中数学解题中如何应用数形结合进行深入研究，并罗列了一些应用实例。

［关键词］初中数学；数形结合；解题方法

［中图分类号］ G633.6 ［文献标识码］  A ［文章编号］ 1674-6058（2023）26-0032-03

初中数学课程主要由代数与几何两大部分构成，前者属于“数”，后者属于“形”，两者是存在一定联系的，这种联系就叫作数形结合，在一定条件下数和形能够相互转化。在初中数学解题训练中，教师需要求学生以认真阅读题目内容与审清题意为前提，根据实际情况与解题需求灵活应用数形结合，使其通过以数解形或以形助数的方式找准解题的切入点，确定解题思路、制订解题方案，进而在数形结合的助力下迅速完成解题，提高做题的正确率。

一、应用数形结合解决绝对值问题

绝对值是学生步入初中阶段后学习的第一个比较抽象的知识点，指的是一个数在数轴上所对应点同原点的距离，一般用符号“[]”来表示。学生刚刚接触绝对值时学习和理解起来难度较大。而且数轴是一个把数和形结合到一起的新型工具，学生缺乏对其的应用经验，在解题时极易遇到困境。在初中数学绝对值问题解题教学中，教师可指导学生借助数轴清晰准确地看到点到原点之间的距离，应用数形结合的方式顺畅完成问题解答。

［例1］已知[x<0]，[y>0]，且[x]的绝对值小于[y]的绝对值，则[x+y]的值是（ ）。

A.正数 B.负数    C. 0    D.难以确定

分析：这道题目难度一般，不过初中生比较缺乏解答有关绝对值题目的经验，如果仅仅凭空想象是难以快速、精准解答的。此时教师可提示学生应用数形结合的方法，根据题干描述把[x]与[y]的位置在同一个数轴上标出来，使其在直观观察中即可轻松判断出[x+y]的值。

解：根据题意在图1数轴上标出[x]与[y]的位置，由图可以看出[x]点到原点之间的距离明显小于[y]点到原点之间的距离，因此可以判断[x+y]的值是一个正数，故正确答案为A选项。这样不仅可以让学生从图形角度来直观理解绝对值的实际含义，还能够让他们掌握处理数轴上任意两个点的距离问题的技巧。

二、应用数形结合解决不等式问题

在初中数学教学中，学生对于不等式知识并非十分陌生，因为他们在小学阶段就学过有关“大于”和“小于”的知识。初中阶段的不等式知识难度与深度均有所增加，涉及更多的不等符号与不等式组等内容，相应的习题难度也在提升。教师可引导学生应用数形结合的方法分析与处理不等式问题，通过画图精准、清晰地展现题中存在的不等关系，进而摆脱解题困境。

A. [x≥-2] B. [x≤9]

C.[ x≥-2]且[x≤9] D. [-2≤x≤9]

分析：本题是一道典型的求解不等式组的习题。学生往往可以处理单个不等式的求解问题，但在求两个不等式解集的公共集时会遇到一定的难度。此时，教师可指引学生应用数形结合的方法完成解题，即结合数轴的直观特点把两个不等式解集之间的公共集展示出来，从而求得准确结果。

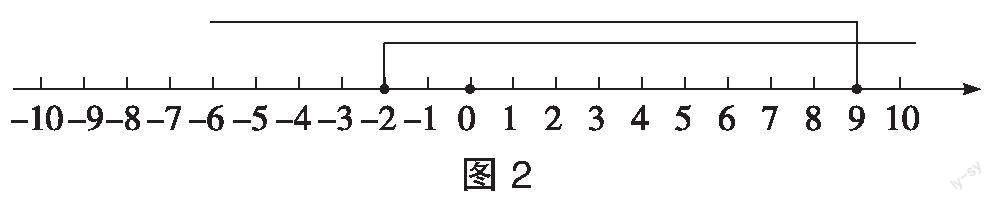
解：在这一不等式组中，求得第一个不等式[3x-1≥x-5]的解集为[x≥-2]，第二个不等式[2x+7≥3x-2]的解集为[x≤9]；将这两个不等式的解集在同一个数轴上表示出来（如图2），可以直观地看到不等式组的解集为[-2≤x≤9]，故选D。

三、应用数形结合解决坐标问题

平面直角坐标系是学生步入初中后学习的新知识，属于数轴的升级版，由横轴[x]轴与纵轴[y]轴组成，同样有原点、正方向与单位长度。在初中数学解题训练中，坐标问题难度相对较大，它能融入多个知识点，综合性较强。教师可引导学生应用平面直角坐标系来进行数形结合，以提高解题效率。

［例3］已知一条直线和一条抛物线的解析式分别是[y=x-1]，[y=x2+2x-2]，求它们的交点坐标。

分析：学生可先画出一个平面直角坐标系，再尝试画出这两个函数图象的草图，发现交点所处的位置在第三、四象限，由于所求的是两者交点，故可将解析式联立起来求解。

四、應用数形结合解决函数问题

函数在初中数学中属于难度比较大的一类知识点，也是学生在初中阶段接触到的新知识。初中函数以基础性函数知识为主，涉及的概念、图象、性质等均是高中函数的前提内容，而函数图象本身即为数与形的有机结合，所以说数形结合是解决函数问题的一个比较常用的解题技巧。初中数学教师可指导学生应用数形结合的方法准确找到函数中点的坐标及变量关系等，进而顺畅解题。

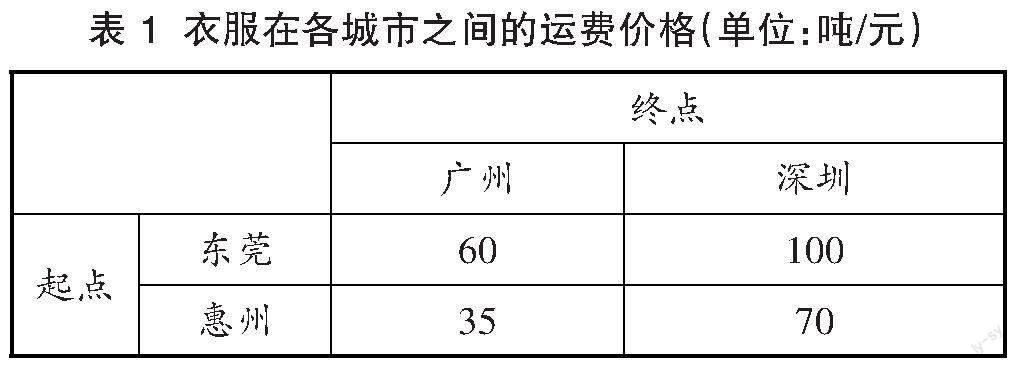
［例4］某一服装厂计划把生产的衣服以物流方式运送至外地销售，其中深圳和广州两个城市分别需要8吨和6吨衣服，惠州和东莞存储的衣服则分别为4吨和10吨，衣服在各城市之间的物流运费价格如表1所示。如果想要一起满足深圳和广州两个城市的衣服需求量，最少需要花费多少运费？

分析：本题题干的信息与条件较多，学生短时间内很难找到解题的切入点。其实本题从本质上看就是一道典型的一次函数题，而解答本题的关键之处在于精准找到衣服质量和运费两者之间存在的关系，由此建立一次函数模式，再根据表达式在平面直角坐标系中画出函数图象，即可轻松求出最少运费。

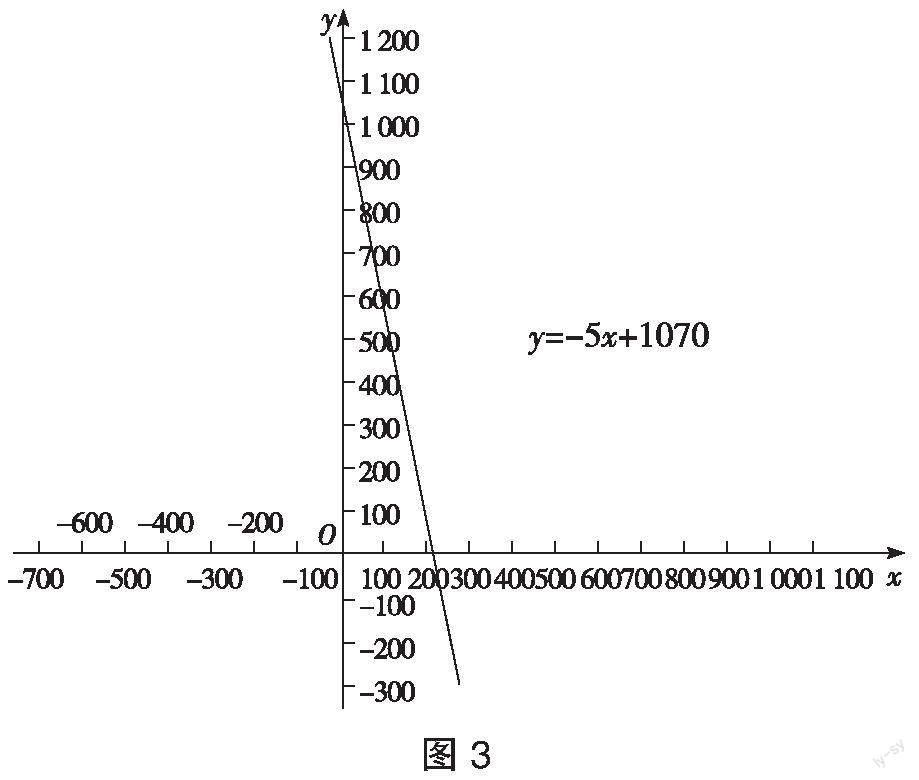
解：设从东莞运往广州的衣服质量为[x]吨，所需运费为[y]元，根据题意可列出一次函数表达式[y=60x+100（10-x）+35（6-x）+70（x-2）]，整理、化简之后得到[y=-5x+1070]，然后画出这一函数的图象（如图3）；根据题目要求确定[x]的取值范围为[2≤x≤6]，通过对该函数图象的观察可以发现该函数为递减函数，这说明[x]值越大，[y]值则越小，所以当[x=6]时[y]值最小，[y=-5x+1070=-5×6+1070=-30+1070=1040]，即当从东莞往广州运6吨衣服时花费的运费最少，为1040元。

五、应用数形结合解决三角形问题

学生在小学阶段就学习了不少关于三角形的基础性知识，如三角形的种类以及边、角之间的关系等，而初中数学中涉及的三角形知识更为多变、复杂，包括大量的性质和定理，题目考查范围有所扩大，学生需具备更高的解题水平。在初中数学三角形问题解题训练中，教师应引领学生应用数形结合的方法，借助“以数解形”精准找到解题的突破口以及快捷、简便的解题思路与方法，高效解决三角形问题。

［例5］已知[a]，[b]，[c]为三角形[ABC]的三条边，且关于[x]的方程[a（x2-1）-2cx+b（x2+1）=0]有两个相等的实数根，那么三角形[ABC]是一个什么形状的三角形？

分析：这是一道判断三角形形状的几何类试题，题干中提供了有关这个三角形三边关系的方程，因此可借助数形结合中“以数解形”的方式进行分析，最终确定该三角形的三条边关系，从而判断出它的形状。

解：先把方程[a（x2-1）-2cx+b（x2+1）=0]转变为一般式[（a+b）x2-2cx-（a-b）=0]，因为这个方程有两个相同的实根，故[Δ=0]，即[Δ=4c2-4（a+b）-（a-b）=4c2+4（a+b）·（a-b）=4（a2+c2-b2）=0]，从而得到[a2+c2=b2]，根据勾股定理能够判断出三角形[ABC]是一个斜边是[b]的直角三角形。

六、应用数形结合解决面积类问题

求图形面积是学生从小学就开始接触的一类数学题目，初中数学中仍然较为常见，但是涉及的图形种类变多，难度增强，计算流程繁杂，学生不仅要掌握基本的运算法则，还要采用一定的面积解题技巧，数形结合即为一个比较常用的方法。初中数学教师在平时的图形面积类问题解题教学中，需重点培养学生应用数形结合方法进行解题的能力，使其能根据题干中提供的条件展开深度分析，准确确定数和形的对应关系，进而顺利解答面积类问题。

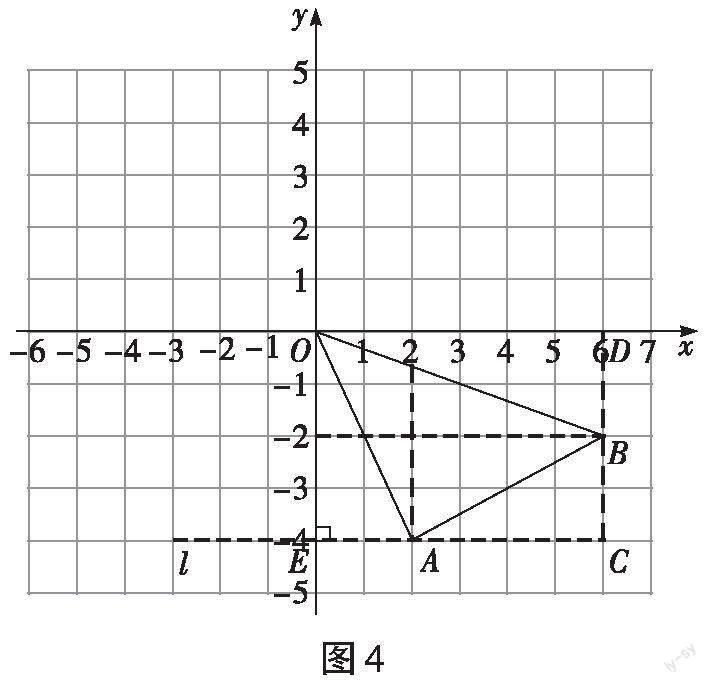
［例6］如图4，在平面直角坐标系中有一个三角形[AOB]，[A]，[B]两点的坐标分别为（2，-4），（6，-2），请求出三角形[AOB]的面积。

分析：解题时，可直接应用数形结合的方法在原图中添加辅助线，即过点[A]画一条水平线[l]，与[y]轴相交于点[E]，过点[B]画一条[x]轴的垂线，与直线[l]相交于点[C]，与[x]轴相交于点[D]，由此得到四边形[ECDO]的面积为24，根据[S△AOB=S矩形ECDO-SRt△ABC-SRt△OEA-SRt△ODB]就能够求出三角形[AOB]的面积大小。

解：在图4中添加辅助线，过点[A]画一条水平线[l]，与[y]轴相交于点[E]，过点[B]画出[x]轴的一条垂线，与直线[l]相交于点[C]，与[x]轴相交于[点D]，可以得到[OE=CD=4]，[EA=2]，[CE=6]，[BD=2]，[CA=CE-EA=6-2=4]，[BC=CD-BD=4-2=2]，那么[S矩形ECDO=6×4=24]，

七、应用数形结合解答几何证明题

数形结合在初中数学解题中应用空间十分广泛，既可以借助图形优势来解答代数题，还可以利用数学运算解答几何证明题。几何证明题是初中数学解题训练中难度系数较高的题型，学生解答此类题目时需综合运用所学知识和逻辑思维能力。教师可以引导学生应用数形结合的方法，结合数学定理与法则进行合理推导，进而破解难题困境。

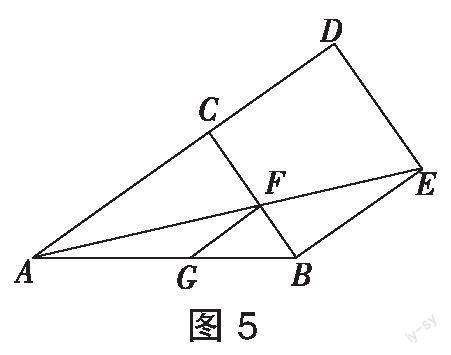
［例7］如图5，在三角形[ABC]中，[∠ACB]为直角，四边形[BCDE]为一个正方形，点[F]为[AE]与[BC]的交点，点[G]为线段[AB]上的一个点，其中[AC]和[GF]为平行关系，请证明[CF=GF]。

分析：要想证明本题中所求的结论，可将原图形拆解成两个三角形，即三角形[ABE]与三角形[ADE]，虽然[CF]和[GF]这两条线段所处的三角形不为全等关系，但是题中给出了平行关系，这时可以应用数形结合的方法，根据比例线段进行推导，从而证明结论。

解：根据题意可以证明三角形[ABE]和三角形[AGF]为相似关系，由此能够得到[GF]∶[EB]=[AF]∶[AE]，再结合题目条件可以证明三角形[AFC]和三角形[ADE]同样为相似关系，由此能够得到[CF]∶[DE]=[AF]∶[AE]，故[GF]∶[EB]=[CF]∶[DE]，因为在正方形[BCDE]中[EB]=[DE]，所以[CF=GF]。

总的来说，在初中数学解题教学中，教师应充分意识到数形结合的作用和价值，在讲授理论知识的过程中渗透数形结合思想，帮助学生扎实理论知识根基的同时做好数学思想的铺垫，了解数形结合的内涵、本质与使用方法，并能用來解答绝对值、不等式、函数、三角形、面积与几何证明等题目，继而提高他们的解题效率。

［   参   考   文   献   ］

［1］  张维军.“数形结合法”在初中数学解题中的应用［J］.数理天地（初中版），2023（7）：29-30.

［2］  黄汉财.妙用数形结合 让初中生数学解题思路更清晰［J］.数理化解题研究，2023（2）：8-10.