再谈圆锥曲线与函数、不等关系的综合考查

栾功　颜紫叶　肖玉霞

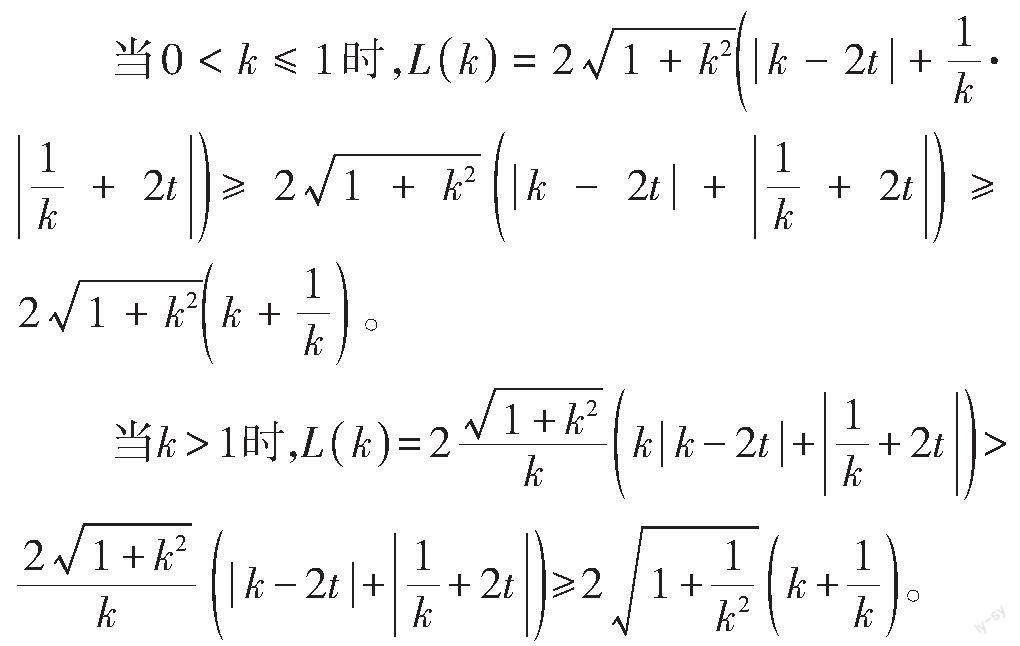
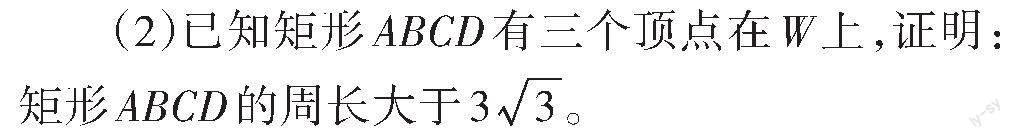
［摘 要］文章通过对2023年新高考Ⅰ卷数学第22题的解法进行探究，揭示了2023年新高考数学试题的一大新亮点：圆锥曲线与函数、不等关系深度综合，为2024年高三数学复习备考提供参考。

［关键词］圆锥曲线；函数；不等关系；综合考查；新高考

［中图分类号］ G633.6 ［文献标识码］  A ［文章编号］ 1674-6058（2023）26-0001-03

新时代背景下的教学改革与高考评价改革同向同行。随着全国各省新一轮教材的使用，截至2023年7月，全国已有29个省份启动新高考改革。近4年新高考数学试题的命题在逐步趋于稳定的同时，突出了一些新的亮点。笔者在本刊2023年第20期的文章中以2023年全国甲卷理科第20题为例论述了2023年高考数学试题的一大亮点：解析几何与函数深度综合。下面笔者以2023年新高考Ⅰ卷数学第22题为例，再谈2023年高考数学试题的另一大新亮点：圆锥曲线与函数、不等关系深度综合。

一、 试题呈现

（1）求[W]的方程；

分析 试题第（1）问以考生熟悉的抛物线的定义为知识背景，考查抛物线的概念和求动点轨迹方程的基本方法；第（2）问将一个边长可变的矩形与抛物线结合，考查矩形周长的最小化问题，看似是考生熟悉的弦长问题，实则极具创新性，将圆锥曲线中的弦长问题与绝对值函数、三角函数、导数研究函数的性质深度综合，注重思维过程，突出考查考生的数学素养，有助于拔尖创新人才的选拔。

二、试题溯源

题源1 （新人教A版数学选择性必修第一册第146页“复习参考题3”第10题，图略）已知直线与抛物线[y2=2pxp>0]交于[A]，[B]两点，且[OA⊥OB]，[OD⊥AB]交[AB]于点[D]，点[D]的坐标为[2，1]，求[p]的值。

题源2 （2002年全国高中数学联赛第13题，图略）已知点[A0，2]和抛物线[y2=x+4]上两点[B、C]，使得[AB⊥BC]，求点[C]的纵坐标的取值范围。

题源3 （1998年上海市高中数学竞赛第三大题，图略）已知在抛物线[y=x2]上有一个正方形的三个顶点[A]、[B]、[C]，求这个正方形面积的最小值。

题源1源于教材习题，与上述试题在几何特征上有相同的本质，都是直角三角形与抛物线相结合，区别在于题源1是确定性问题，而上述试题是双动点问题，源于教材而高于教材，起到引导教学、回归教材的作用。题源2与题源1相比，由确定性问题上升为动态问题。题源3与上述试题几乎相同，历年的竞赛试题往往蕴含着丰富的数学思想方法，一线教师需引起重视。

三、 解法探究

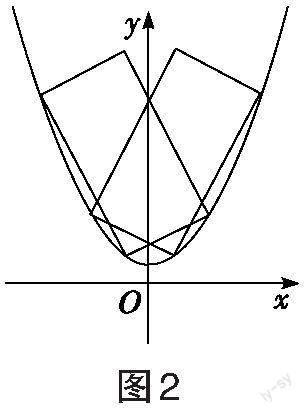
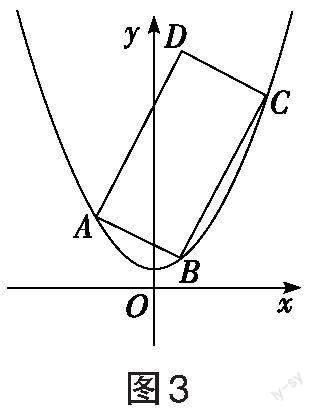
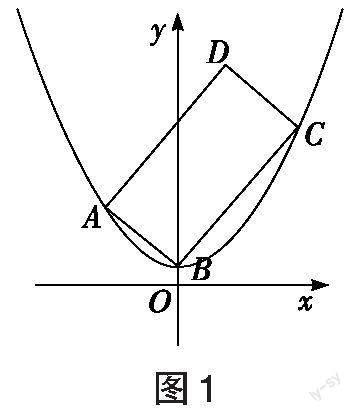
对于复杂的问题，考生可先从较为特殊的情况入手探寻思路。如图1所示，本题最特殊的情况就是矩形有一个顶点和抛物线的顶点重合，与题源1相同，考生自然清楚这是关于直线[BC]斜率[k]的函数问题。由于本题中矩形与抛物线搭接形式的开放性，我们需要顺势思考更为一般的情况。如图2所示，矩形的四个顶点有三个顶点在抛物线上，则这三个点不可能同时出现在[y]轴的同侧，结合抛物线的对称性，从逻辑意义上我们不妨只考虑图3的情况，记点[A、B、C]在抛物线上，且点[A]在[y]轴的左侧，点[B]、[C]依次出现在[y]轴的右侧。下面从不同角度设参求解。

评析：设线求解弦长是解答这类问题的通性通法，大部分考生都会想到这一步，解题困难主要在于矩形周长取值范围的求解。由于矩形边长的可变化性，致使矩形周长的表达式出现了双变量，这让绝大部分考生望而却步。该解法选择先固定主元再求解的思路，是解决双变量问题的常见方法。在具体的函数最值求解过程中，不论是去绝对值的分类讨论，还是运用导数求解目标函数的单调性，都将函数与圆锥曲线的综合体现得淋漓尽致。试题命制之新颖，解答之根本，都无不让人赞叹不已。

评析：该解法建立在洞悉试题背后的数学本质之上，通过两个“不妨设”和代数代换，避免了解法1的分类讨论，体现了“多想少算”的命题意图，对考生的数学思维能力要求较高。

评析：该解法的本质是借助直线的方向向量探寻矩形[ABCD]有三个顶点落在抛物线上的充要条件，对考生的动态思维能力和化归与转化问题的能力要求较高。

四、 回顾反思

回顾以上解法，解题思路皆源于对相关数学概念本质的理解，进一步探究，便有如下思考：

我们可做如下尝试：

这里巧妙地借助[k]的范围对表达式进行初步放缩，从而接着利用三角不等式放缩消元，将二元函数问题转化为一元函数问题。试题巧妙地将解析几何、函数、不等关系融合在一起，加大了对数学思维的考查，为不同层次的考生发挥水平提供了空间。

思考3 新时代下的高三数学复习教学的重心在哪里？从解题分析来看，试题的命制源于基础性、本源性知识，发展于各知识模块之间的联系。从新高考试题体现的这两大亮点来思考，高三复习教学的重心应落在基本概念、公式、原理等本源性知识的理解上，落在知识体系的构建上，落在学生思维能力的培养上。当然，高一、高二基础年级的教学更应如此。

［   参   考   文   献   ］

［1］  2002年全国高中數学联赛［J］.中等数学，2002（6）：19-24.

［2］  李大元，刘鸿坤，熊斌，等.1998年上海市高中数学竞赛［J］.中等数学，1999（3）：28-29.

［3］  教育部教育考试院.高考试题分析：数学：2024年版［M］.北京：语文出版社，2023.