核心素养指引下的中职学生数学思想培养探析

杜杰

摘要：“授人以鱼，不如授人以渔”，学生只有领会数学思想，掌握科学的数学学习方法，养成良好的思维习惯，才能真正形成数学学习能力，有效地应用知识解决各种数学问题。文章围绕任意角的三角函数教学内容的基本特征，通过从特殊到一般、从复杂到简单、从数字到图形的教学设计，培养学生的数学思想，并强调数学思想的培养要遵循过程性原则、持续性原则、参与性原则、反复性原则、可操作性原则。

关键词：中职数学；数学思想；任意角；三角函数；设计；反思；原则

中图分类号：G712文献标志码：A文章编号：1008-3561（2023）29-0113-04

数学是中职学校的公共基础课程，为学生提供继续学习、发展所需的数学知识、技能、方法、经验和思想，其具有基础性、应用性、发展性和职业性等特点。中职数学不仅是传授数学知识的载体，更承担着培养学生发现和提出问题、分析和解决问题能力等功能。单纯的知识教学只会让学生实现知识的累加，而掌握学习方法以及数学思想就会使学生受益终身，正所谓“授人以鱼，不如授人以渔”。学生只有领会了数学思想，掌握数学学习方法，养成良好的思维习惯，才能形成较强的数学学习能力，有效应用知识解决各种数学问题。本文以“任意角的三角函数”为例，探究核心素养指引下的中职学生数学思想培养策略，以期为中职数学教学工作者提供教学方法借鉴。

一、中职数学核心素养内容及培养学生数学思想的意义

中职数学学科核心素养包括数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析六个方面。其是一个有机的整体，但彼此之间又相互独立、相互交融。

随着新课程改革的推进，数学教育不能仅满足于对学生进行知识与技能的培养，还要以理性思维育人，着重于对学生的数学思想、学习方法和数学核心素养的培养[1]。掌握数学思想就是掌握数学的精髓，其不仅可提升学生发现问题、解决问题等能力，还能发展学生的数学思维，让学生领悟到数学的真谛。所以，教師应着眼于引导学生用数学的眼光观察世界、用数学的思维思考世界、用数学的语言表达世界。

二、三角函数的学科价值与数学思想

三角函数是描述客观世界中周期性变化规律的重要数学模型，在其他学科领域也有广泛应用。“任意角的三角函数”定义是高中数学的核心概念之一，其是完成“任意角和弧度制”后的新授课内容，是后续学习三角函数关系的推导、三角函数的图像与性质的基础，可以说，该章节内容起到的是承上启下的作用[2]。在学习三角函数的过程中，部分学生存在不理解、不会运用等情况，究其原因，是学生对三角函数的认知还停留在初中的函数问题上。数学思想是解决数学问题的基本策略，是提高学生解题能力的关键，无论是建立概念，发现规律，还是解决问题，都离不开数学思想、方法的支持与帮助，而基于数学核心素养有意识地培养学生的数学思想可让学科知识、技能转化为学生一生都受用的能力和素养[3]。在教学实践中，教师可融入数形结合思想、类比思想、函数思想、转化思想等，引导学生探索知识的形成过程，着重培养学生的数学思想和数学核心素养。

三、三角函数教学中数学思想的培育

掌握数学思想是促使学生将知识应用于实践的基础[4]。下面，笔者以转化思想为例，分别从特殊到一般、复杂到简单、数字到图形的转化，探究在三角函数教学中培养学生数学思想的策略。

1.从特殊到一般

任意角的三角函数是在学完“任意角和弧度制”后的一节新课，中职数学课程将角的概念进行了推广，而本节教学内容是将初中学过的锐角的三角函数的相关知识拓展到任意角的三角函数。因此，笔者在进行课堂教学时，利用学生熟悉的锐角三角函数引入任意角的三角函数，以唤醒学生的知识记忆，帮助学生完成从熟悉到陌生、从特殊到一般的过渡。

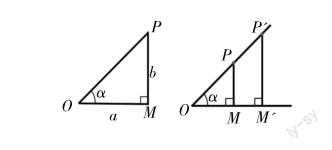
2.从复杂到简单

对于任意角琢，当角琢的终边落在第一象限时，通过在角琢的终边上任取一点构造直角三角形，再结合锐角的三角函数的定义，分别表示出角琢的三个三角函数，这样，学生比较容易理解。当角琢的终边落在第二象限、第三象限、第四象限或角琢为界限角时，通过构造直角三角形，按照锐角的三角函数的定义去表示角琢的三角函数，对学生来说，理解起来比较困难。所以，笔者根据学情对任意角的三角函数的定义推导过程进行了调整，只讨论角琢的终边落在第一象限时的定义，对其他情况不再详细推导，而是鼓励学有余力的学生课后自主探索，以突出本节课的教学重点。

在教学过程中，笔者将学生初中学过的锐角的三角函数定义放到平面直角坐标系中讨论，有效引导学生完成了从三角形到坐标系的转化，同时也为学生在平面直角坐标系中定义任意角的三角函数搭建了平台。

3.从数字到图形

数形结合思想是一种基本数学思想，其具备直观、形象、简捷等诸多优点。“数缺形时少直观，形少数时难入微”，数形的相互转化可将几何问题用代数的方法处理，或者通过几何图形来解决代数问题，不仅有助于学生整合数学知识，还能增强学生的创新思维。在“任意角的三角函数”教学中，笔者就运用数形结合思想，教学设计思路是由锐角的三角函数定义引出任意角的三角函数定义，由相似三角形的性质说明锐角的三角函数值与角终边上点的位置是没有关系的，具体如下。

（1）任意角的三角函数的定义。在教学实践中，笔者由锐角的三角函数过渡到任意角的三角函数，将锐角放在平面直角坐标系中加以说明。此时，角的终边落在第一象限，在角的终边上任取一点，构造直角三角形，进而转化为用点的坐标表示角的三角函数。

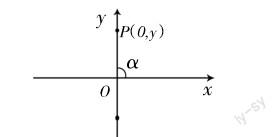
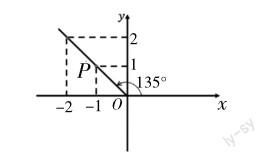
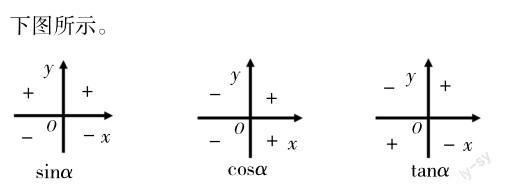
根据任意角的三角函数定义，得出任意角的三角函数值在各象限内的符号并不难，但对于中职生来说，记住每个象限内的三角函数值的符号是难点。因此，笔者在课堂上向学生介绍了三种不同的记忆方法。方法1：按照第一象限、第二象限、第三象限、第四象限的顺序，可用四个字“全”“是”“天”“才”记忆符号为正的三角函数值，即第一象限全正、第二象限sin琢为正、第三象限cos琢为正、第四象限tan琢为正；方法2：将“刁”字的书写顺序与sin琢、cos琢、tan琢相对应，跨越的象限符号为正。方法3：根据口诀“一全二正弦、三切四余弦”，记住符号为正的情况。

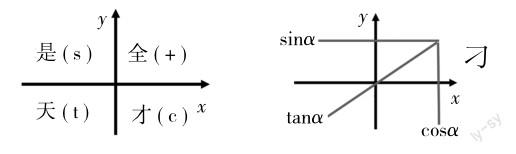
四、三角函数数学思想培育的教学反思

在核心素养背景下，教师在中职数学教学中，应积极创新，整合教学资源，渗透数学思想、方法，以多样化的教学方式，引导学生掌握数学逻辑，具备理性的数学思维，不断提高学生的数学核心素养[5]。在实际教学中，数学思想的渗透要遵循以下几项原则。

1.过程性原则

数学思想是依赖于数学问题而存在的。在实际教学中，为充分发挥数学思想的作用，教师必须做到以下几点。第一，要正确认识数学思想的应用价值。生活中的数学问题无处不在，而数学思想是解决实际应用问题的重要手段。第二，在运用数学思想解决数学问题时，教师要引导学生发现、认识以及总结数学思想，使学生逐步形成个性化的思维体系，并做到融会贯通，举一反三，即实现“授之以渔”。例如，“曲线与方程”的概念具有很强的抽象性和逻辑性。教师可引导学生结合数形转化思想，将数学题目进行数化形的转化，然后充分利用图形的直观性特点，合理运用课程知识点，形成科学的解题思路。

2.持续性原则

教师在设计教学活动时，要根据学生已有的知识储备，科学规划，合理设计教学内容，同时，教学方法要系统，具有可持续性，不能设定太高的起点，要让学生“跳一跳，够得到”。数学思想的渗透要循序渐进，不能急于一时，避免“灌输式”教学，达到“先学后用”的目的，使学生的数学思考能力逐渐提升。

3.参与性原则

在中职数学课堂上，要想使数学思想得到有效渗透，必须激发学生的学习热情。因此，中职数学课堂教学要坚持“参与”的原则，既要充分调动学生的学习热情，又要尊重学生在课堂上的主体性，指导学生根据自身的认识与能力，对数学理论知识进行探索与实践。例如，在教学“解一元二次不等式ax2+ bx+c>0”相关问题时，二次项系数a是否为0是讨论的重点内容，但学生往往忽略对a的讨论，在此过程中渗透分类讨论思想尤为重要。教师要适当引导，让学生在探索过程中发现问题，并体会分类讨论思想的重要性。

4.反复性原则

构建数学思想的应用体系不能一蹴而就，需要反复练习、反复积累、反复总结，教师在教学中要为学生创造锻炼的机会。例如，在求解集合的交集、并集、补集时，教师可利用数轴呈现集合元素之间的关系，反复引导学生运用数形结合思想解题。再如，针对不同类型的习题，教师可引导学生运用同一种数学思想方法进行解答，如二次函数二次项系数a相关问题、等比数列求前n项和中公比q是否为1的问题、判断曲线方程为椭圆或双曲线的问题等，都可用到分类讨论的思想。

5.可操作性原则

在实际教学中，教师要根据教学内容、学生的实际学习情况以及教学实践灵活渗透数学思想，并适时调整。例如，求点P（3，3）关于直线y=-2x+2的对称点P的坐标时，有的学生会先画出直线，通过作图的方法找到点P的对称点，但不能精确得到对称点的坐标。教师要及时提示学生将形转为数：直线PP與y=-2x+2是垂直的，且PP的中点在直线上，通过互相垂直的直线斜率乘积为-1以及中点坐标公式，即利用方程思想就可求得点P的坐标。

五、结语

总而言之，数学思想是分析、处理和解决数学问题的根本方法，是对数学规律的理性认识，数学思想在中职数学教学中具有积极意义。教师要在教学设计中渗透数形结合思想、类比思想、函数思想、转化思想，同时合理提出问题，创设情境，让学生主动探索新知，并在探索的过程中真正理解和掌握数学知识和技能、数学思想和方法，实现核心素养的提升。

参考文献：

[1]贺霞，蔡择林.基于“三教”的高中数学概念教学实践探索———以“任意角的三角函數”教学为例[J].高中数学教与学，2019（12）： 18-21.

[2]孙帮兰.“任意角的三角函数”概念教学的分析与建议[J].中学数学，2019（21）：12-13.

[3]杨子圣.高中数学教育重在培养数学能力与数学思想等核心素养[J].人民教育，2022（23）：77-78.

[4]刘玉文.关注数学思想渗透凸显核心素养培养———以2019年高考三角函数试题为例[J].中学数学研究，2020（03）：6-9.

[5]杨宏胜.同课异构“角”上生花———以“任意角的三角函数”的教学为例[J].高中数学教与学，2019（23）：1-2+9.

Exploration on the Cultivation of Mathematical Thought Among Secondary Vocational School Students Guided by Core Competence

———Taking "Trigonometric Functions at Any Angle" as an Example

Du Jie

（ Hangzhou Xianlin Vocational High School ， Zhejiang Province， Hangzhou 310000， China）

Abstract： "Teaching people to fish is better than teaching them to fish." Only by understanding mathematical ideas， mastering scientific mathematical learning methods， and cultivating good thinking habits can students truly form mathematical learning abilities and effectively apply knowledge to solve various mathematical problems. The article focuses on the basic characteristics of the teaching content of trigonometric functions at any angle， and cultivates students mathematical thinking through teaching designs from special to general， from complex to simple， and from numbers to graphics. It emphasizes that the cultivation of mathematical thinking should follow the principles of process， continuity， participation， and repetition， operability.

Key words： secondary vocationalmathematics； mathematical ideas； any angle； trigonometric function； design； reflection； principle