用导数研究函数的极值和最值高考真题分析
——以2022年全国乙卷理科第16题为例
2022-11-19江苏
江苏 龚 亮
高考数学命题依据《普通高中数学课程标准(2017年版2020年修订)》,突出、落实“综合性”考查要求,突出对主干、重点知识和内容的考查,发挥高考试题对中学教学改革的引导和促进作用.2022年全国乙卷理科第16题是一道突出“综合性”考查要求的导数应用试题.这里,以该试题为母题,就导数研究函数的极值、最值问题中的应用进行探究.
一、母题呈现
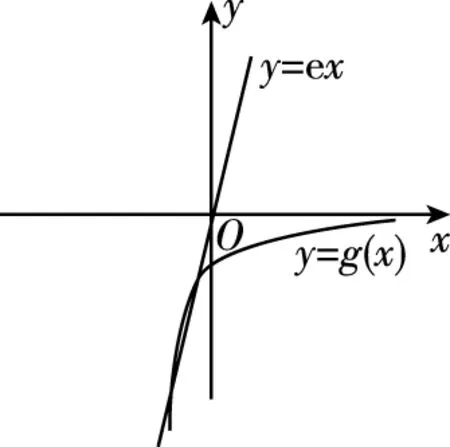
(2022·全国乙卷理·16)已知x=x1和x=x2分别是函数f(x)=2ax-ex2(a>0且a≠1)的极小值点和极大值点.若x1 函数的极值和最值是利用导数研究函数性质的两个重要应用,母题是以函数极值点的大小关系为题设背景设计的应用导数求参数取值范围问题.解答母题首先要理解函数“极值点”的概念,并在对a分类讨论的基础上,将函数“极值点”转化为导函数“零点”,再转化为相应方程的“根”,进而通过构造函数,转化为函数图象有两个交点,数形结合或利用函数的最值求解.解答母题要运用函数与方程、化归与转化、数形结合等数学思想,对数学抽象、逻辑推理、直观想象、数学建模及数学运算等数学核心素养的要求较高. 思路1:由x1,x2分别是函数f(x)=2ax-ex2的极小值点和极大值点可得,当x∈(-∞,x1)∪(x2,+∞)时,f′(x)<0,当x∈(x1,x2)时,f′(x)>0,再分a>1和0 解法1:因为f(x)=2ax-ex2(a>0且a≠1), 所以f′(x)=2axlna-2ex=2(axlna-ex). 因为x=x1和x=x2分别是函数f(x)=2ax-ex2的极小值点和极大值点, 所以f′(x1)=f′(x2)=0,且函数f(x)在(-∞,x1)和(x2,+∞)上单调递减,在(x1,x2)上单调递增, 所以当x 若a>1,当x<0时,2lna·ax>0,2ex<0,则此时f′(x)>0与当x 由f′(x1)=f′(x2)=0,可知x=x1和x=x2是方程f′(x)=0,即2(axlna-ex)=0的两根, 所以函数y=axlna与函数y=ex的图象有两个不同的交点,且交点的横坐标分别为x1和x2. 令g(x)=axlna,则g′(x)=axln2a,0 设过原点且与函数y=g(x)的图象相切的直线的切点坐标为(x0,ax0lna),则切线的斜率为g′(x0)=ax0ln2a, 解法2:因为x1,x2分别是函数f(x)=2ax-ex2的极小值点和极大值点,所以x1,x2分别是导函数f′(x)的两个零点,即x1,x2分别是方程f′(x)=0的两个根,且x1 由解法1知a>1不符合题意,所以0 导数及其应用是中学数学的核心内容,也是每年高考考查的重点和热点,无论是客观题还是解答题,多数情况下处于压轴题的位置,起着“把关定向”的作用.高考数学“成也导数,败也导数”是导数试题重要性的真实写照.极值和最值是函数的两条最重要的性质,用导数研究函数的极值和最值更是高考命题考查的热点,常常在同一个题中同时考查.除上述母题外,还有2021全国乙卷理科第20题:“设函数f(x)=ln(a-x),已知x=0是函数y=xf(x)的极值点. 另外需要指出的是,母题的函数中出现了一般指数函数“ax”的形式,这在全国卷中不足为怪,但在新高考卷中却鲜有涉及,主要是以特殊指数函数“ex”的形式呈现,这或许是全国卷与新高考卷的一点差异吧,2023年高考由全国卷转为新高考卷的地区的师生在复习备考中应特别关注一下. 若母题的题设条件不变,结合母题的解法2,设计求函数最值的取值范围,则有: 若改变母题中的函数形式,同时不明确两个极值点的属性和大小关系,则有: 变式2:已知函数f(x)=ex(aex-1)+x(a>0)有两个极值点x=x1和x=x2,则实数a的取值范围为________. 解析:因为f(x)=ex(aex-1)+x,所以f′(x)=2ae2x-ex+1, 令t=ex,t∈(0,+∞),则令f′(x)=0可得2at2-t+1=0,则判别式Δ=1-8a. 则当x∈(-∞,x1)时,f′(x)>0,当x∈(x1,x2),f′(x)<0,当x∈(x2,+∞)时,f′(x)>0,此时函数f(x)有两个极值点,符合题意, 若改变母题中的题设函数,设计函数存在极值,且极值为正数,则有: 变式3:已知函数f(x)=aln(x+1)-xex(a≠1)有极值,且极值为正数,则实数a的取值范围为________. 解析:函数f(x)的定义域为(-1,+∞). 当a≤0时,f′(x)<0,所以f(x)在(-1,+∞)上单调递减,所以f(x)无极值. 所以f′(x)在(-1,+∞)上单调递减. 又f′(0)=a-1,f′(a-1)=1-aea-1. ①当0 当-1 ②当a>1时,f′(0)>0,f′(a-1)<0,同理符合题意. 综上,可得a>0且a≠1. 故实数a的取值范围是(0,1)∪(1,+∞). 若改变母题中的函数形式,设计判断两个极值的差是否有最小值的探索性问题,则有: 解析:f(x1)-f(x2)无最小值,理由如下: 函数f(x)的定义域为(0,+∞). 设g(x)=-x2+x-a. 因为函数有两个不同的极值点x=x1和x=x2, 所以方程-x2+x-a=0有两个不同的根x=x1和x=x2, 因为f(x1)-f(x2)的最小值为f(x)极小值-f(x)极大值,不妨设f(x1)为极小值,f(x2)为极大值, 故f(x1)-f(x2)不存在最小值. 导数是解决函数问题的有力工具,运用导数研究函数的极值与最值等问题是高考命题的一类热点题型,常常处于压轴题的位置.这里,将函数的极值与最值相关的知识和注意事项加以归纳整理. 1.利用导数研究函数极值、最值的思维程序 2.利导数求函数y=f(x)在某个区间上的极值 利导数求函数y=f(x)在某个区间上的极值的步骤: ①求导数f′(x); ②求方程f′(x)=0的根x0; ③检查f′(x)在方程f′(x)=0的根x0的左右的符号:“左正右负”⟺f(x)在x0处取极大值;“左负右正”⟺f(x)在x0处取极小值. 利用导数研究函数的极值问题时要注意f′(x)=0为极值点的必要非充分条件.判断极值时,一定要结合函数的单调性来判断,避免出现错误.如果函数在x=x0处满足f′(x0)=0,若导函数的值在该点附近符合“左正右负”,则x0是极大值点;若符合“左负右正”,则x0是极小值点. 3.求函数f(x)在[a,b]上的最值 若函数f(x)在[a,b]上连续,在(a,b)上可导,则求函数f(x)在(a,b)上的最值的步骤: ①求函数f(x)在区间[a,b]上的极值; ②将求得的极值与f(a),f(b)比较,得到f(x)在区间[a,b]上的最大值与最小值. 利用导数研究函数的最值时应注意:①函数的最值是对整个定义域而言,是在整个取值范围内讨论问题,是一个整体性的概念;②函数在其定义域区间上的最大值、最小值最多各有一个. 4.由函数的极值或最值求参数取值范围二、母题分析
三、母题解答




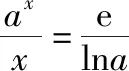
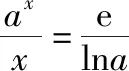

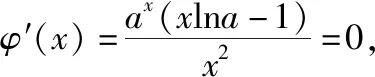

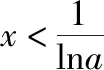

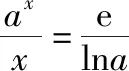
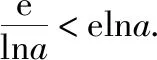


四、考查模式

五、母题变式


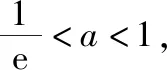


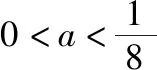
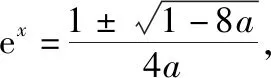
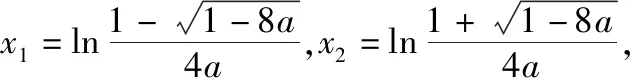

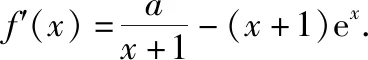







六、方法规律


