浅谈解题教学的“过程”教学

湖南 欧阳才学

“解题教学”，就是通过典型数学题的学习，去探究数学问题解决的基本规律，使学生会像数学家那样“数学地思维”.“解题教学”是数学教学的重要组成部分，数学教学离不开“解题教学”.通过“解题教学”，不仅可以使学生加深对所学知识的理解，而且有利于促进学生数学核心素养的形成和发展.

数学“解题教学”不应是“结果”的教学，而应是“过程”的教学，在“解题教学”过程中，教师不能只告诉学生每一步如何做，而是要把为什么这么做,把所思、所想的“思路历程”展现给学生，让学生经历一次探索、解决问题的过程，教会学生如何通过自己的分析获得解题思路.

那么，如何体现解题教学的“过程”呢？本文通过以下两个案例来说明.

【案例1】如图1，已知在圆锥SO中，底面半径r=1，母线长l=4，M为母线SA上的一个点，且SM=x，从点M拉一根绳子，围绕圆锥侧面转到点A.

(1)求绳子的最短长度的平方f(x)；

(2)求绳子的最短长度的最小值和最大值.

答案：(1)f(x)=x2+16(0≤x≤4);(2)最小值为16，最大值为32.

思路探索:

①题目给出的是已知底面半径、母线长的圆锥，需要求的是圆锥侧面上两点A,M间所拉绳子的最短长度(两点间的最短距离)，如何来求最短长度？在圆锥侧面上“绕来绕去”恐怕很难确定何时长度最短.如图2，沿母线SA将圆锥的侧面展开，“化曲为直”，连接AM即为绳子的最短长度.

②绳子的最短长度AM“找到”了，可如何用x表示它的平方呢？

由图2可以看出，只好“交给”△ASM了.在△ASM中，已经知道SA=l=4，SM=x,

那么，现在的关键就是去求侧面展开图——扇形的圆心角∠ASA′了.怎样求出∠ASA′？这可能是许多同学“为难”的地方.下面我们一起解决掉这一难点.

我们知道，扇形是圆的一部分，圆周角是360°，只要知道扇形占所在圆的“份额”，扇形的圆心角就能够求出来了.

这里，扇形所在的圆以圆锥母线的长SA=l=4为半径，则扇形所在圆的周长C=2πl=8π；而扇形的弧长即圆锥底面圆的周长C′=2πr=2π.

③求出∠ASA′=90°，在△ASM中利用勾股定理就可以用x表示出绳子的最短长度AM的平方f(x).由于M为母线SA上的一点，且SM=x，所以0≤x≤4.

④根据f(x)和x的取值范围，利用函数知识求出f(x)的最小值和最大值，进而求出绳子的最短长度的最小值和最大值.

通过上述的思路探索，请同学们完整地写出解题步骤.

这样设计本题的讲解，能让学生感悟知识生成、发展与变化的过程，训练学生真正理解和掌握数学知识与技能、数学思想与方法，获得广泛的数学经验.

分析：观察所求函数式的特点，先通过取倒数拼凑，再用均值不等式求解.

对于如此的“解题教学”，我们肯定会有疑问：分析中所说的“特点”是什么？“取倒数拼凑”出什么？“均值不等式”在哪？解题中，怎么想到“x→3x”的呢？不知道学生听完后会不会晕，笔者的感觉是如此高超的解题技巧令人叹服，只是不知道这样的方式在课堂上讲解会不会让学生对数学望而生畏？如果笔者是学生的话，多半会感觉数学难度很高，很难想到这种解法！这样的讲法让不少学生远离数学，吓跑学生是迟早会发生的事！

笔者认为，“解题教学”有个原则：从学生思维的最近发展区入手，展示教师的“思维过程”，行使教师的“传道授业解惑”职责，因此，从大多数学生的想法也就是平时所说的通性通法来考虑也许会更好！

思路探索:

也就是说利用我们熟悉的“二次方程根的存在性与分布问题”已经解决了这个问题：

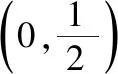
拓展：一般地，求分母为二次式的分式函数的最值时，可以将待求的函数值先看成常数，并把分式函数转化成二次方程，利用判别式法解决.

探究：我们处理分子、分母都在变的分式函数，常规想法是把分子(或分母)变成常数来处理，这样可以把分母改用1+x表示，并上下同除以(1+x)2，其过程：

分子、分母同时除以(1+x)2，

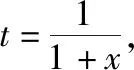
小结：方法2是化归与转化思想的具体体现，其实质依然是二次函数的最值问题.