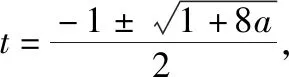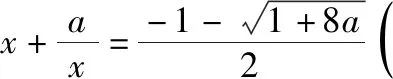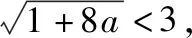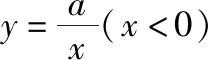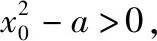多思维切入 妙角度拓展——以一道零点问题的探究为例

江苏 韩文美

函数零点问题是函数与方程中的基本知识和重要内容，一直是历年高考中的热点和重点问题之一．此类问题内容丰富、融合度高、交汇性强、创新度高，同时又能合理渗透高中数学中重要的数学知识与思想方法，有机融入函数与方程思想、“动”与“静”之间的合理转化等辩证思维，是充分体现与考查数学知识及数学能力的一个好场所，备受各方关注．

1．问题呈现

【问题】(2022·浙江省温州市普通高中高考适应性测试数学试题(温州二模)·17)已知a>0，函数f(x)=x4+x3+ax+a2有且仅有两个不同的零点，则a的取值范围是________．

此题以含参的四次函数为问题背景，结合参数的取值限制，利用函数的零点个数情况来确定参数的取值范围，难度较大．具体解决问题时，可以通过函数的图象思维、方程思维、解析几何思维以及不等式思维等不同的思维方式来切入，结合零点的个数情况进行综合分析与判断，实现参数的取值范围的确定．

2．问题破解

思维视角一：图象思维

方法1(图象转化法1)：

解析：由f(x)=0，可得x4+x3=-a(x+a)，

结合函数f(x)=x4+x3+ax+a2有且仅有两个不同的零点，可知函数g(x)=x4+x3与直线y=-a(x+a)的图象有两个不同的交点，

又g(-1)=g(0)=0，可得函数g(x)的大致图象，如图所示，过点A(-1，0)，O(0，0)，

由a>0，可得直线y=-a(x+a)与x轴负半轴交于点B(-a，0)，

结合图象可得，函数g(x)的图象与直线y=-a(x+a)相切时有且仅有一个交点，易得切点为A(-1，0)，此时B(-1，0)，

所以当a=1时，函数g(x)的图象与直线y=-a(x+a)相切，结合直线y=-a(x+a)的斜率与零点的关系，数形结合可知，当01时，函数g(x)的图象与直线y=-a(x+a)没有交点，所以a的取值范围是(0，1)．

解后反思：根据函数所对应的方程，结合零点情况拆分为一个函数与一条直线的交点个数问题，进而利用函数图象的单调性与直线的位置关系来直观分析，数形结合，巧妙转化，是解决此类高次函数零点问题中比较常用的解题技巧．正确的拆分与转化是关键所在，动直线是其中一个比较常见的问题．

方法2(图象转化法2)：

解析：由于a>0，当x≥0时，f(x)=x4+x3+ax+a2≥a2>0，

根据题目条件，可知函数f(x)有且仅有两个不同的负零点，

由f(x)=0，可得x4+x3+ax+a2=0(x≠0)，

又g(-a)=0，可得函数g(x)的大致图象，如图所示，同时在同一平面直角坐标系中作出二次函数y=-(x2+x)的图象.

数形结合可知，只需-1<-a<0，即0

解后反思:根据分离函数法，将函数有两个零点的问题转化为两个函数图象有两个公共点问题，然后运用数形结合直观地求出参数的取值范围．这里分离函数中将求复合函数参数的取值范围问题转化为一个含参的复合函数以及一个常见的二次函数图象的交点变化与个数确定问题，从而运用数形结合解决问题．

思维视角二：方程思维

方法3(换元法)：

解析：由f(x)=0，可得x4+x3+ax+a2=0(x≠0)，

解后反思：根据函数所对应的方程，通过恒等变换处理，利用换元转化为二次函数方程，结合二次函数求根公式，通过根的性质以及函数零点的个数情况构建对应的不等式，通过求解不等式来确定参数的取值范围．合理的利用恒等变换方法进行处理为问题的进一步分析与解决提供一定的思维依据，变换的过程往往是朝着熟知的知识方向进行．

方法4(方程转化法)：

解析：由于a>0，当x≥0时，f(x)=x4+x3+ax+a2≥a2>0，

根据题目条件，可知函数f(x)有且仅有两个不同的负零点，

由f(x)=0，可得x4+x3+ax+a2=0(x≠0)，

所以a的取值范围是(0，1)．

解后反思:根据函数所对应的方程，通过恒等变换，将函数零点问题转化为方程的根的问题来处理，利用二次方程的判别法求得参数的取值范围．再利用参数条件以及函数的特征确定函数具有两个不同的负零点，是解决问题的关键所在，为后面进一步的方程求根指明方向，回避不必要的分类讨论．

思维视角三：解析几何思维

方法5(距离转化法)：

解析：由于a>0，当x≥0时，f(x)=x4+x3+ax+a2≥a2>0，

根据题目条件，可知函数f(x)有且仅有两个不同的负零点，

由f(x)=0，可得x4+x3+ax+a2=0(x≠0)，

所以a的取值范围是(0，1)．

解后反思：根据函数所对应的方程，通过恒等变换，合理配方，利用配方后关系式的结构特征，将问题转化为相应曲线上的点到定点距离为定值的点的个数问题，利用图形直观想象，数形结合得出参数的取值范围．通过距离这一特殊结构特征，合理构建，数形结合直观处理，更加简洁有效．

思维视角四：不等式思维

方法6(均值不等式法)：

解析：由于a>0，当x≥0时，f(x)=x4+x3+ax+a2≥a2>0，

根据题目条件，可知函数f(x)有且仅有两个不同的负零点，

由f(x)=0，可得x4+x3+ax+a2=0(x≠0)，

即x2+2x+a<0，

结合判别式Δ=4-4a>0，解得a<1，即0

所以a的取值范围是(0，1)．

解后反思:根据函数所对应的方程，通过恒等变换，将函数零点问题转化为方程的根的问题来处理，借助均值不等式的转化以及因式分解进行变形与转化，得以确定对应的不等式成立，利用方程的判别法构建不等式来确定参数的取值范围．合理借助均值不等式的放缩与转化，为问题的解决提供更加直接有效的途径．

3．变式拓展

探究1：保留题目创新情境，改变参数a的限制条件为一般性条件，由“a>0”拓展为“a∈R”，使得问题的分类与研究更加广阔，从而得到以下更为一般性的变式问题．

【变式1】已知a∈R，函数f(x)=x4+x3+ax+a2有且仅有两个不同的零点，则a的取值范围是________．

解析：当a=0时，由f(x)=x4+x3=x3(x+1)=0，可得x=0或x=-1，函数f(x)恰有两个不同的零点；

当a>0时，由以上问题的方法5，可得a的取值范围是(0，1)；

探究2：根据变式1及其解析过程，在一般条件下进行全面系统地讨论对应函数的零点个数问题，从而得到以下对应的变式问题．

【变式2】已知a∈R，试讨论函数f(x)=x4+x3+ax+a2的零点个数情况．

具体解析过程可以参照原问题的解析与变式1中的解析过程，得到以下对应的结论：

(2)当a=1时，函数f(x)有且仅有一个零点；

4．教学启示

(1)总结常规方法，归纳常见思维

解答一些函数零点的相关问题时，最常用的方法就是借助函数的图象，数形结合直观解决，利用合理代数运算与恒等变换，转化为比较熟知的基本初等函数问题或可以求导确定函数单调性的对应函数问题等，巧妙分离参数，合理做到一“静”一“动”或一“直”一“曲”，“动”直线，“静”曲线，巧平移，妙变换．借助函数的图象，“直”“曲”分离，数形结合，“动”“静”配合，直观想象．

(2)倡导“一题多解”，实现“一题多得”