函数与导数零点问题中的易错分析与教学探讨
2022-11-19湖北
湖北 周 威
导数综合问题中的零点个数问题在高考中常以解答压轴题的形式出现,教师在关注不同层次考生得分的同时,还要关注这类问题中如何体现对学生分类讨论思想、数形结合思想、化归与转化思想、函数与方程思想等数学思想的考查,包括学生应用这些数学思想时的思维错乱或脱节情况.本文以2022届高三一次大型跨区域联考的导数综合题为例,分析解答过程中学生容易出现的4种典型易错类型,并提出相应的解决策略,提高不同层次考生在导数综合问题中的得分率.
一、试题呈现

(1)证明:f(x)在(1,+∞)上有且仅有一个零点;
(2)假设常数λ>1,且满足f(λ)=0,试讨论g(x)的零点个数.

(易错类型1:不能恰当选择自变量的值来确定函数值的正负,从而确定不了零点的取值范围)

①当a<0时,
(易错类型2:不会对参数进行恰当界点的分类)
g″(x)>0,g′(x)在(0,+∞)上单调递增.因为g′(1)=-2a>0,g′(e2a)=2a(1-e2a)<0,则存在x0∈(e2a,1)使得g′(x0)=lnx0-2ax0=0,即lnx0=2ax0,所以当x∈(0,x0)时,g′(x)<0;当x∈(x0,+∞)时,g′(x)>0,即g(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增;
(易错类型3:不会自设“隐零点”进行讨论)
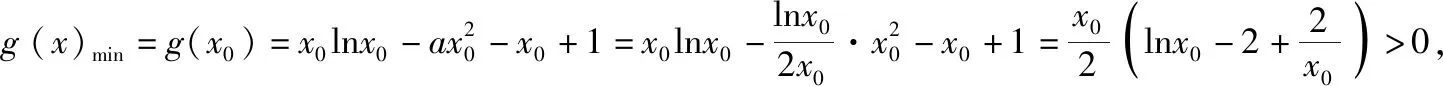
②当a=0时,
g(x)=xlnx-x+1,g′(x)=lnx,令g′(x)=0,得x=1,可得g(x)在(0,1)上单调递减,在(1,+∞)上单调递增,g(x)min=g(1)=0,只有一个零点.
③当a>0时,


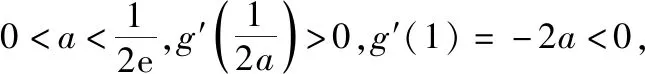
(易错类型3:不会自设“隐零点”进行讨论)

所以g(x)在(0,m)上单调递减,在(m,n)上单调递增,在(n,+∞)上单调递减.
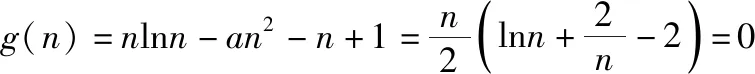

(易错类型4:不能将参数用已知条件表述出来)
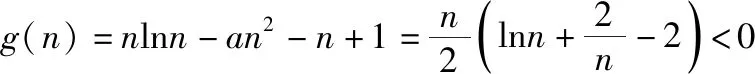
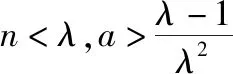
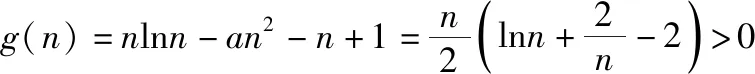

(易错类型2:不会对g(n)与界点“0”进行分类讨论)

解法二(分离参数法):
令g(x)=0,即xlnx-ax2-x+1=0,从而有a=
(易错类型4:不能将参数用已知条件表述出来)
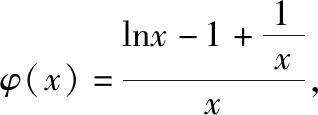

结合(1)可知,φ(x)在(0,1)上单调递减,在(1,λ)上单调递增,在(λ,+∞)上单调递减.
(易错类型3:不会根据“隐零点”进行单调性讨论)
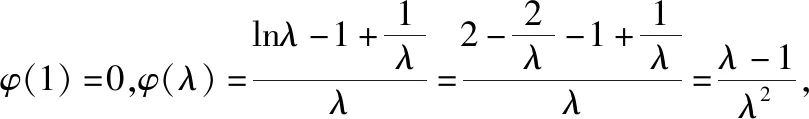
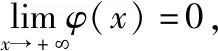

当a<0时,g(x)没有零点;
(易错类型2:不会对参数进行恰当界点的分类)


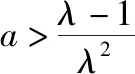
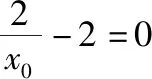
二、试题数据分析与错因分析
1.考试数据分析
本题属于跨地市区域联考,不区分物理方向和历史方向的考查结果为均分1.6分,属于难题.具体数据如下表:

参考人数小题小题分值平均分157752第(1)问31.4第(2)问90.2

难度系数区分度满分人数零分人数0.50.723095521330.020.1282136843
2.错因分析
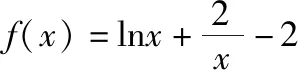

三、易错练习
1.相同命题立意下含“单参”变式练习
【例2】已知函数g(x)=xlnx-ax2-1(a≥0).
(1)当a=0时,讨论g(x)的单调性;
(2)当g(x)恰有两个零点时,求a的取值范围.

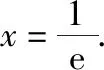
(2)解法一(分类讨论法):
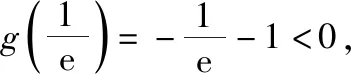


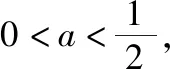
因为g(m)=mlnm-am2-1=am2-m-1<0,

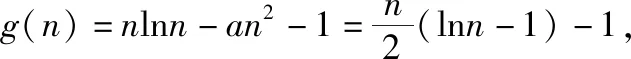

当g(n)>0时,此时n>4.32且0 当g(n)<0时,此时n<4.32且a>0.29,g(m)<0且当x→0时,g(x)<0,g(x)没有零点. 综上所述,当0 解法二(分离参数法): 令φ(x)=xlnx-x-2,则φ′(x)=lnx,令φ′(x)=0,则x=1,所以φ(x)在(0,1)上单调递减,在(1,+∞)上单调递增.又φ(1)<0,φ(e)<0,φ(e2)=e2-2>0,当x→0时,φ(x)<0,故φ(x)在(e,e2)上有唯一的零点x0.根据所给数据4.32×(ln4.32-1)≈2,从而x0≈4.32. 所以当x∈(0,4.32)时,h′(x)>0,即h(x)在(0,4.32)上单调递增; 当x∈(4.32,+∞)时,h′(x)<0,即h(x)在(4.32,+∞)上单调递减. 且当x→+∞时,h(x)→0,且当x→0时,h(x)→-∞, 所以当0 【评注】命题意图虽然类似,但函数形式发生了变化,题中也没有将“隐零点”直接给出,而是给出了近似计算参考数据,要求学生对a的临界值进行近似值估算,并根据近似值进行分类讨论.高考导数综合题中出现近似计算的情况也并不少见,教学中可以进行尝试.对于含“单参”的导数综合题,依然需要引导学生进行“参数分离”的尝试,特别是在加入了近似计算的情况下,“感觉会做”与“算出来”的效果差距很大! 2.类似含“双参”变式练习 【例3】(2021·新高考Ⅱ卷·22改编)已知函数f(x)=(x-1)ex-ax2+b. (1)讨论f(x)的单调性; (2)若a>0,讨论f(x)的零点个数. 【解析】(1)因为f′(x)=x(ex-2a),令f′(x)=0,x=0或x=ln2a,所以 当a≤0时,f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增; 当b 当b=a(ln22a-2ln2a+2)时,f(ln2a)=0,函数f(x)有两个零点; 当a(ln22a-2ln2a+2) 当b=1时,f(0)=0,函数f(x)有两个零点; 当b>1时,f(0)>0,函数f(x)有一个零点. 当b>a(ln22a-2ln2a+2)时,f(ln2a)>0,函数f(x)有一个零点; 当b=a(ln22a-2ln2a+2)时,f(ln2a)=0,函数f(x)有两个零点; 当1 当b=1时,f(0)=0,函数f(x)有两个零点; 当b<1时,f(0)<0,函数f(x)有一个零点. 【评注】当遇到含有“双参”的函数零点个数问题,分离参数、数形结合或者“对数单身法”就可能会失去效能,这时分类讨论是解决问题的首选基本技能,特别是其中某一大类又要分成很多小类,那么如何做到有效、全面和不重复分类,需要教师和学生在“讨论”的做题过程中去深刻领悟. 对于导数综合题的零点个数问题,由于涉及多类问题特征(包括单调性、特殊位置的函数值符号、隐零点的探索、参数的分类讨论等),需要学生对多种基本方法、基本思想、基本技能进行整合,从而解题难度相对较大,再加之考试时间紧张,绝大部分学生在导数综合题的得分为0,但是如果把握好策略性知识复习的有效性,提高不同层次考生的得分率,效果也应该是各专题中最明显的! 1.做细解题过程的易错类型归类 导数在判断函数零点个数的作用主要体现在通过极值的正负与函数单调性判断函数图象走势,从而判断零点个数.就导数综合题中零点问题的易错类型,一般可参照例1解题过程归为4类,对不同题型、不同解法的解题过程,可对照这4个易错类型从思维的角度进行归类,建立思维痛点和易错点之间的联系,才能提高解题效率. 2.加强分类讨论思维的步骤训练 对于导数综合题,分类讨论才算得上是真正的通性通法.很多同学习惯了规避分类讨论的解题套路,在真正遇到需要思维深度的例题(比如例3)时,依然束手无策,在解题过程中要形成如下分类讨论的思维步骤:对哪个参数分类?在什么情况下分类讨论?分类的界点怎么确定?分类是否全面?通过具体实例、设问层层递进,引导学生经历、领悟分类讨论思维步骤的过程,特别是在思维痛点处、易错点处适当搭建脚手架,让学生逐步逼近分类讨论思想的本质. 3.落实一题多解与变式迁移训练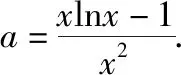





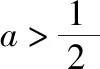



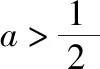
四、教学复习策略

