解读尺规作图，类题探究感悟

季叶红

[摘  要] 尺规作图在中考试题中较为常见，同时尺规作图有着独特的教学价值，不仅可以巩固学生的基础知识，同时作图过程是思维与实践的结合，有助于提升学生的思维能力. 文章解读了尺规作图，并结合实际开展问题探究，深入感悟，提出了几点建议.

[关键词] 尺规作图;实践;角平分线;垂直平分线

问题解读

尺规作图是中考的高频考点，能够全方位考查学生的能力，即阅读理解能力、作图实践能力、知识应用能力，以及逻辑思维能力. 问题设计特点鲜明，要求学生利用尺规来绘制图形，从根本上可归为作角的平分线、垂直平分线、全等三角形、构建特殊线段长等，掌握基本的作图方法是关键.

近几年在实际考查时将作图实践与计算推理、开放设计相结合，提升了问题的综合性，要求探究学习要深刻理解作图的方法原理，挖掘问题本质;准确定位考点，构建作图思路;结合图形特性开展推理，确保作图“有理”，分析“有据”.

探究剖析

尺规作图综合题的类型较为众多，解析过程需要充分阅读题干信息，把握作图的关键，在此基础上分析作图思路，下面笔者结合实例深入探究，分步剖析作图过程.

1. 类型一：数轴作图，数值比较

例1 （2021年江苏省盐城市中考卷第21题）如图1所示，A是数轴上表示实数a的点.

（1）用直尺和圆规在数轴上作出表示实数的点P（保留作图痕迹，不写作法）;

（2）利用数轴比较和a的大小，并说明理由.

分析：本题的难点是作图表示的点，作图的关键是确定的线段长，然后利用圆规画弧定点到数轴上. 比较和a的大小只需观察在数轴上的位置关系即可.

过程剖析：（1）第一步——线长构建

以表示1的点为圆心，单位长为半径作圆，利用线段的垂直平分线作出高，则可以构建直角边为1的等腰直角三角形，由勾股定理可知斜边长为，从而完成线长构建，见图2中的虚线.

第二步——数值定位

以点O为圆心，线长（虚线）为半径画弧，与数轴正半轴的交点就为点P，如图2所示.

（2）由于点A位于点P的右侧，故a>.

解后总结：对于数轴上特殊值点的确定问题，通常先作直角三角形，利用勾股定理来构建特殊值的线段长;然后结合圆的性质，通过画弧来实现等线段转化.

2. 类型二：综合作图，函数求值

例2（2021年江苏省无锡市中考卷第24题）如图3所示，已知锐角三角形ABC中，AC=BC.

（1）请在图3①中用无刻度的直尺和圆规作图：作∠ACB的平分线CD;作△ABC的外接圆☉O（不写作法，保留作图痕迹）;

（2）在（1）的条件下，若AB=，☉O的半径为5，则sinB=______. （如需画草图，请使用图3②）

分析：本题中作图要注意△ABC为等腰三角形，（1）问需要作角平分线，属于基础作图，而作△ABC的外接圆☉O，则需要确定△ABC的外心，而外心是三角形三条垂直平分线的交点. 在本题目中CD为AB的垂直平分线，只需再作另一边的垂直平分线即可. （2）问求sinB，可将其放在直角三角形中，结合圆半径、AB长求线段比例即可.

过程剖析：（1）第一步——作角平分线

利用尺规作∠ACB的角平分线CD，与AB的交点设为E，实则CD也是AB的垂直平分线（如图4所示）;

第二步——作垂直平分线

利用尺规作线段AC的垂直平分线，与CD的交点就为三角形的外心（三角形任意两边垂直平分线的交点为外心），也是三角形外接圆的圆心（如图4所示）.

第三步——作外接圆☉O

以点O为半径，AO长为半径画圆即可（圆心O到三角形顶点的距离均相等），如图4所示.

（2）在Rt△AEO中，已知AO=5，AE=AB=，由勾股定理可得OE==，所以CE=EO+OC=. 在Rt△CEB中使用勾股定理，可得BC==8，所以sinB==.

解后总结：上述解析的关键是理解三角形的外心为对应外接圆的圆心，“垂直平分线上的点到线段两端距离相等”是作图构建的基础. 而在实际求解时无须作三边的垂直平分线，利用两线定交点即可完成.

3. 类型三：画弧定点，构形分析

例3（2021年江苏省常州市中考卷第23题）如图5所示，B，F，C，E是直线l上的四点，AB∥DE，AB=DE，BF=CE.

（1）求证：△ABC≌△DEF;

（2）将△ABC沿直线l翻折得到△A′BC.

①用直尺和圆规在图中作出△A′BC（保留作图痕迹，不要求写作法）;

②连接A′D，则直线A′D与l的位置关系是______.

分析：下面主要探究第（2）问尺规作图及位置关系分析，作△A′BC与△ABC关于直线l对称，故为全等关系，只需確定点A′的位置即可，而点A′由A′B和A′C的长度限制，即到点B和点C的距离是一定的，故可利用圆规作圆弧来确定.

过程剖析：①第一步——定线段AB画弧

以点B为圆心，AB长为半径画弧，则该弧上各点到点B的距离均等于AB长;

第二步——定线段AC画弧

以点C为圆心，AC长为半径画弧，则该弧上各点到点C的距离均等于AC长;

第三步——交点定点A′

显然两弧的交点到点B和点C的距离分别等于AB和AC，就为满足条件的点，即点A′.

②过点A′作A′M⊥l，过点D 作DN⊥l，如图6所示，根据上述作图过程可知△A′BC≌△ABC≌△DEF，从而可知A′M=DN，且两线平行，所以四边形A′MND为平行四边形，所以A′D∥l.

解后总结：上述实则是通过作图构建全等三角形，故需要满足两边对应相等，可采用两段画弧相交定点的方式. 该种方式也可用于构建不同位置的全等三角形，即首先任意定量一条线段，确定三角形其中两个顶点，然后两端画弧确定第三个顶点.

4. 类型四：作图设计，开放思维

例4（2021年江苏省无锡市中考卷第24题）如图7所示，已知P是☉O外一点. 用两种不同的方法过点P作☉O的一条切线. 要求：

（1）用直尺和圆规作图;

（2）保留作图的痕迹，写出必要的文字说明.

分析：本题为开放型的作图题，要过点P作圆的切线，把握核心特性，若切点为Q，则∠PQO=90°，作图时可立足直角三角形的特征——斜边中点到切点的距离等于斜边的一半.

过程剖析：

方法1——垂直平分线+画弧定点

第一步——作PO的垂直平分线

连接PO，作OP的垂直平分线，与OP的交点设为A，则点A为OP的中点;

第二步——画弧定切点，连切线

以点A为圆心，PA长为半径画弧，与☉O的交点就为切点Q，连接PQ，就为满足条件的切线（AP=AO=AQ），如图8所示.

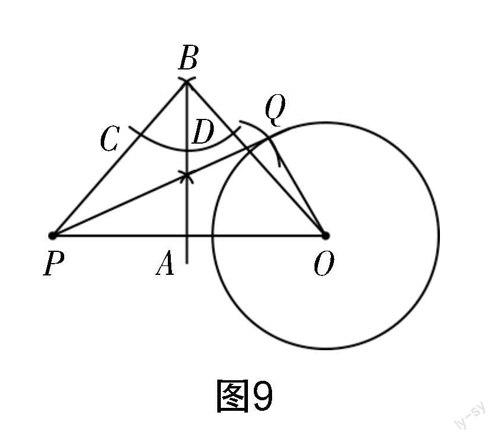
方法2——等腰三角形+角平分线+画弧定点

第一步——作等腰三角形

作以OP为底边的等腰三角形BPO;

第二步——作中点A

作出∠OBP的角平分线，与OP的交点为A（AB就为PO的垂直平分线，AP=AO）

第三步——画弧定切点，连切线

以点A为圆心，PA长为半径画弧，交☉O于点Q，连接PQ，就为满足条件的切线（AP=AO=AQ），如图9所示.

解后总结：上述作图的核心是作三线段相等，故围绕垂直平分线、角平分线和画弧来组合设计方案. 作图设计为开放型问题，往往设定几何特性，作图的过程方法不唯一，但作图过程要立足定理、思路清晰.

感悟建议

尺规作图是數学文化中的璀璨明珠，直观地呈现了几何的图形魅力，作图过程可以充分反映学生的思维，可全面考查学生的定理理解、实际操作能力及创新意识. 教学中要引导学生，积累作图经验，理解作图原理，故笔者提出以下几点建议.

1. 掌握基本作图，积累作图经验

从上述典例探究中可知，众多基本作图方法是破解综合题的关键，故教学探究中教师要引导学生总结基本的作图方法，结合具体问题积累经验. 如常见的作角平分线、垂直平分线、两段画弧定交点等.

2. 几何知识分析，理解作图原理

作图过程中隐含了几何的知识定理，正是在几何定理的支持下完成了作图构建，因此学生只有理解作图原理才能从根本上掌握作图方法. 教学中教师可从基本作图方法入手，引导学生利用几何知识分析方法原理，如垂直平分线作图原理是两段弧的交点到线段两端点的距离相等.

3. 挖掘问题本质，激活创新思维

尺规作图综合题的破解过程，需要挖掘问题本质，准确定位根本特性. 如上述例4作切线，构建直角三角形斜边中点到顶点的线段关系，并基于该特性构建了两种作图方案. 教学中教师要引导学生透视问题，把握本质，给学生留足思考空间，激发学生的创新思维.

4. 培养逻辑思维，提升核心素养

尺规作图过程中的严谨性、逻辑性十分突出，是逻辑推理与合情推理的融合，教师在尺规作图教学中要注重培养学生严谨思考的习惯，提高学生的逻辑推理能力. 同时教师要渗透图形变化、数形结合等思想，将提升学生的核心素养作为教学根本.