初中数学教材“单元解读”的视角、方法和范式

王婷婷

[摘  要] 初中数学的单元解读是基于核心素养的衍生物，重视教学的主体性，注重执教者个体思想的注入. 而且单元解读的视角、方法和范式直接决定着数学教学质量，因此初中数学很注重单元解读. 文章就初中数学教材中单元解读的视角、方法和范式展开论述并提出相关建议.

[关键词] 初中数学教材;单元解读;视角、方法和范式

引言

初中阶段的学生从生理学角度看绝大部分处于青春期，性格上有些许叛逆，也没有总结过去的能力，而“单元解读”教学法恰好解决了这个问题，从课本规定的单元以及执教者自己组合的单元知识进行教学，提高了学生整合知识的能力以及综合运用能力. 下面针对“单元解读”的各方面进行分析.

单元解读概念解析之教学现状分析

1. 单元解读概念解析

首先，从历史角度看“单元解读”. 它原始起于“单元教学”，19世纪启蒙运动促进了思想解放，更加注重主体性的发挥，从而提出了整体化的教学方法. 这一方法萌芽于比利时教育家德克乐利提出的教学整体化和兴趣中心原则，在1931年美国莫里逊提出“单元教学法”——把学习内容分割成较大的单元，让学生在几天或一周时间内学习一项教材或解决一个问题.

其次，从现代教育看“单元解读”. 现代教育中的单元有两个含义：①以当下教材为蓝本，按照编写者规划的教学顺序进行简单的重组，以便课时之间的配合协作更加紧密. ②以教材内容结构之间的逻辑关系为蓝本，重新组合“大单元”来突出教学的整体性、系统性，并且在新的单元里融入教师对教学内容的创造性思考. 羌达勋认为数学单元教学是基于数学的学科素养，用系统论的方法对教材中所有有联系的内容进行分析、整合、设计和开展单元教学.

最后，从官方解释看“单元解读”. 数学单元教学的定义是这样描述的：指教师以整体教学观和系统论为教学指导，以培养教学学科素养为目标，将关联性强的知识、技能和经验整合为模块（单元）而开展的教学活动. 总而言之，教师主观性的整合与教材本身划分相结合，但是以执教者自行规划为主体展开大模块教学.

2. 现阶段初中数学“单元解读”教学现状分析

首先，数学单元教学提高了教师教学的难度. ①据调查统计，男教师的整体感比女教师整体感要强，男教师擅长宏观把控，女教师恰好是擅长微观教学. 但是当下男女教师分配不平衡，在选择教师行业上，女教师在初中数学教师的占比超过了60%，所以导致初中数学在整体教学方面是个短板. ②当下教师大部分坚持原本的非单元教学，不愿意改变，给“单元解读”教学法的进行造成了困扰，那么单元解读教学的效果和质量是不理想的. ③“单元解读”是把所有有关联的数学知识整合到一个模块进行教学. 但是当下数学教材“知识零碎化”现象严重，而且执教者每个人都有自己的整合标准，在数学课程目标和教材的理解上会产生很大的偏差，这可能会让教师产生偏离“单元教学”的牵引，说白了就是语文写作中的“跑题”. ④在很多知识量大以及单节课教学内容小的矛盾处理上，教师很难把握教材的“分解和集成”. ⑤在传统意义上的教学会有统一的教学进度，但是如果用单元解读教学法就无法保证教学进度的一致性，涉及学校考试也很难做到统一.

其次，数学单元教学给学生带来了挑战. ①数学单元的教学法看中的是整合性，对学生整合信息、推导结论等方面提出了更高的要求. 而且“单元教学法”下的数学学习工程量大，需要掌握的数学知识多，在真实的广度與深度方面给学生带来了阻碍. ②现代教育中考试成绩是重要的选拔标准，通过考试来测验学生的能力，也就是当下教师和学生都注重容易量化的指标，比如知识与技能的考查容易量化，但是都忽视了不容易量化的，如学习策略、情感态度和价值观等评价指标. 这样造成了学生对于自己评价的一种误解，对于学生的学习与教师的教都会产生不好的影响. ③处于初中阶段的学生原认知水平不高是对单元教学的一大挑战. 对教学知识方法和思想认知方面都需要原认知的主动配合与操作，认知和非认知的协同与管理也是需要原认知的参与. 单元教学需要学生整体、系统地看待多个具有独立性的教学知识、方法和思想，需要激活调动协调认知因素和非认知因素，但是当下绝大多数学生原认知水平是很难适应的. ④单元教学下对学生深度学习的要求以及思维的要求、练习的要求都是非常高的，对学生来说都是很困难的. 以上从教师以及学生的角度分析了单元教学法面临的问题，并从主客观角度分析了单元教学法的可行性.

初中数学“单元解读”视角教学

方法呈现

1. 基于“生活数学”的宏观角度，密切联系生活实例

生活与数学是“个体与影子”的关系，也是一对矛盾的主体，两者互相影响、互相制约. 数学是研究数量关系和空间形式的科学，是对客观现象抽象而逐步形成的科学语言与工具. 从这种意义上来说，数学来源于生活，但是高于生活，又服务于生活. 因此，在当下的教学中教师要重视生活与数学的联系，密切联系生活实例.

比如在教学苏教版七年级上册第二章“有理数”中的第一节“负数”这一部分知识时，教师要尽可能让学生从生活中找到“负数”的影子. 在日常生活中，人们坐电梯向上记为正，向下则记为负;电视上广播的天气预报中，某城市天气为-4 ℃～16 ℃，在天气语音广播中是这样读的：某城市天气为零下4 ℃到零上16 ℃，所以在温度中有零上和零下之分，那零下就是负数的概念. 再如，教师教学数轴时，可引导学生将向右移动记为正方向，向左移动则记为负方向. 只要学生善于发现，就不难找到生活中的数学知识.

2. 基于“知识关联”角度，提高学生知识迁移能力

数学这门学科的知识是琐碎的，但是每个零碎的知识点都能追根溯源，好比树的主干与枝干的关系. 只有努力找到每个知识点的归宿，才能让数学知识有其自身的结构与体系. 但是当下教材编写并不是把一个“整体线”有逻辑顺序地展现给大家，而是分开编写，而且知识的学习也是前后联系的，这要求学生在学习知识的时候能够互相迁移.

如学习苏教版七年级下册“一元一次不等式”时，就需要学生联系前面所学习的等式有关知识，虽然两个是不一样的知识点，但有着很强的对比性，也有其内在的联系性，能够帮助学生更好地理解不等式知识. 在不等式第一节中是“生活中的不等式”，要求学生关联生活数学知识，如日常生活中公路路段的最高时速限制、牛奶中蛋白质所含重量的限制等，在不等式的求解方面跟等式是一样的，不过就是把“=”号换成了不等号（“>”“<”“≥”及“≤”），对于学生知识的掌握有很大促进作用.

3. 基于“矛盾转化”的辩证角度，培养学生数学转化思维

数学是一门充满神奇的学科. 数学中包含了特殊与一般、有限与无限、变化与不变、数与形、整体与局部、单一与多样、间接与直接、正与反、一维与多维、简单与复杂等矛盾的主体. 在哲学中常说“矛盾是可以互相转化的”这也适用于数学，在数学教学中，教师要培养学生矛盾转化思维.

比如苏教版八年级上册第一章“全等三角形”，在证明三角形全等时学生可以采用“对顶角相等、內错角相等、同旁内角互补”等法则、原理来进行“角与角”之间的转化. 再如在学习九年级下册“锐角函数”中常见的也是转化法，正弦、正切和余弦之间有一个公式关系即sinα=cosα·tanα，若题目中告诉了正切值，学生就可以用正弦和余弦来代替. 再者在求三角函数的过程中也经常用到转化法. 已知角的度数、正弦值就可以求出正切值或者是余弦值. 利用一个角跟正弦值就能求出边长，进而进行解题.

复习巩固

（1）在A市建设规划图上，城区南北长为240 cm，A市城区南北的实际长为18 km，试写出该规划图的比例尺.

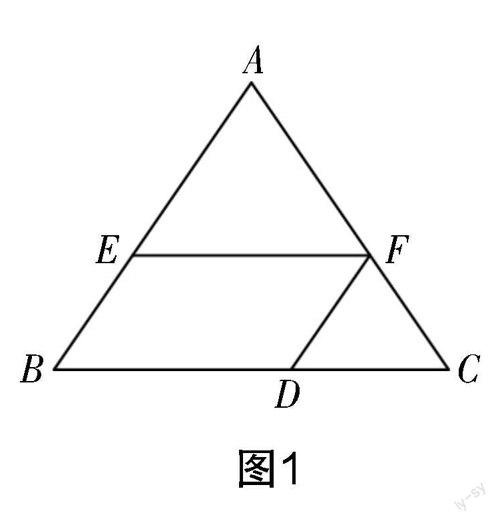
（2）如图1所示，在△ABC中，点D，E，F分别在BC，AB，AC上，且EF∥BC，FD∥AB. 若AE=3.6，BE=2.4，CD=2.8，求BD的长.

这是九年级下册“图形的相似”这一章的习题，题中BD的长度可转化为EF的长度，再利用题中平行条件得出平行四边形，然后计算出长度. 总之，转化在数学上就是把相等的互相转化、意义相同的互相转化、未知的转化为已知的、特殊的转化为一般的，不断借助辩证的哲学思维解决数学题目.

结语

初中数学在新时代素质教育以及核心素养培养号召下衍生出“单元解读”教学法，本文通过了解单元解读的概念以及单元教学的现状，提出密切联系生活实际、提高学生知识迁移能力以及培养转化思维的方法来提高学生整体化学习的效率，以促进教育教学的进步与发展.