复习课教学的三条主线：知识·思维·数史

【摘 要】数学复习课是初中数学教学中不可忽视的重要环节，由于应试教育的冲击，现在的数学复 习课堂很大程度上抑制了学生的思维活动、操作经验和知识素养的提升和发展。面对现状，教师应抓住 知识、思维、数史的主线，还数学复习课堂一个活泼的氛围。

【关键词】初中数学；复习课；尺规作图；知识串联

【中图分类号】G633.6 【文献标识码】A 【文章编号】1005-6009（2015）14-0044-03

【作者简介】张建良，江苏省常熟市教育局教学研究室（江苏常熟，215500）教研员。

数学复习课是整个教学环节中一类十分重要的课型，它既是对学过知识的再巩固和再拓展，也是对学习思维的再梳理和再提升。但为了成绩，应试模式的复习课层出不穷。这限制了学生的思维活动、操作经验、知识素养的提升和发展。那么如何改善这样的复习课堂呢？下面结合笔者所执教的一节初二尺规作图复习课来尝试回答以上问题。

一、教学设想

初二学生已经学习过5种基本尺规作图，为此在进行尺规作图的复习教学设计前主要思考了以下三条主线。

1.“知识”线。

尺规作图的工具只限于直尺和圆规，其核心是通过圆规作等长的线段，达到制图的效果。我们知道几何图形的最基本的元素是“点”，所以尺规作图是通过“作点”来实现的。因此，在解答尺规作图题时，就要分析“点”所满足的条件，然后用作等长的线段来确定点。在完成作图以后，还需找出正确作图的理由，通过对作图目标任务的分析获得正确的作图方案。

2.“思维”线。

尺规作图不仅是一种操作，更是对数学思维和数学探究的过程。在尺规作图中，学生一般先通过分析、预测、判断，再进行画图操作。在探究过程中“为什么要作这样一个点？”“为什么这样作图是正确的？”这两个问题的思考伴随着整个作图的整个过程，从而完成学习自我监控。学生思维的激发还在于有好的问题，一个需要思考的问题往往最能让学生思维活跃起来，是一个有效的思维触点。

3.“数史”线。

数学文化与数学教育是目前很多人关注的话题，数学文化中包括数学史、数学家、数学美以及人类认识和发展数学的过程中体现出来的探索和进取精神等。数学文化的价值主要在于数学对于人们观念、精神及思维方式的养成所具有的影响。因此在教学中让学生接触数学文化，可以了解人类追求知识的步伐，感受数学家锲而不舍的探索精神。其次，接受数学文化的熏陶，也是提升课程目标中情感态度价值观的一个很好的教学支点。

在尺规作图复习课中进行三“线”合一的教学，即一条知识（作图）线，一条思维线，一条数学史线，期许实现更有价值的数学复习。

二、教学片段

片段1 播放微视频

微视频1：基本作图——作已知角的角平分线；

微视频2：基本作图——作已知线段的垂直平分线。

通过以上两个微视频，回答（1）直尺和圆规的作用；（2）“交点”的情形种类；（3）“尺规作图”的由来。

【设计意图】

通过播放基本作图的微视频，一是说出两个尺规作图对应的名称；二是说出直尺画直线，圆规画等长线段的道理；三是说作图中符合条件的关键点；四是说尺规作图中交点的情形，另外在课上介绍关于尺规作图的数学小史。

【教后反思】

通过观看基本作图的微视频，学生没能说出用圆规的本质是获取等长线段。对于交点的各种类型，课上没有讨论到。预设写在纸上，变化却在课上。

片段2 解决问题

问题一：求作一个角等于30°。

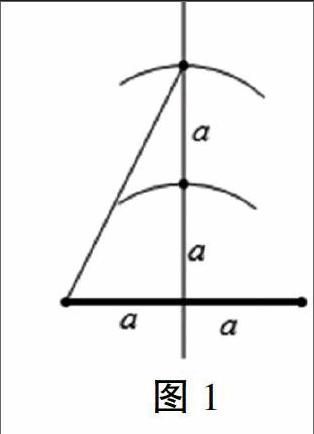
生1：首先作一条线段，然后作该线段的垂直平分线。接着在垂直平分线上，以垂足为圆心、线段一半长为半径作弧与中垂线交于一点；再以该交点为圆心、同样长为半径作弧交于上方部分一点。连接这个交点和线段一端点，夹角就是30°（如图1所示）。

师：图中所作出的角是30°吗？

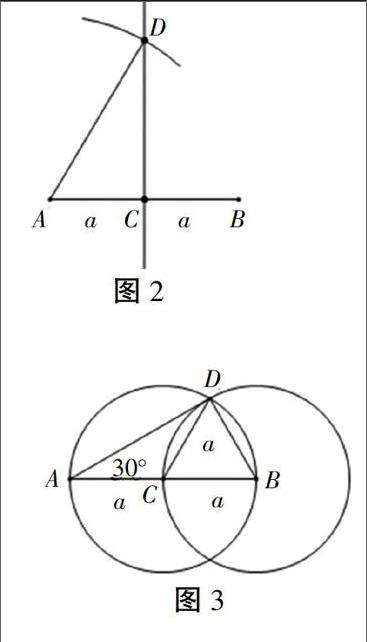
生2：图中所示角不等于30°，因为图中出现的是两条直角边之间有一半关系，而不是一条直角边等于斜边的一半。应以线段的一个端点为圆心，以2a长为半径作弧与垂直平分线交于一点，图中∠ADC的度数等于30°（如图2所示）。

师：还有其他作法展示吗？

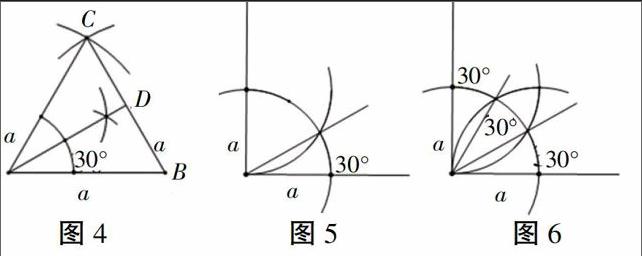
生3：同样作一条线段，并作该线段的垂直平分线。以该线段的一个端点为圆心、以该线段的一半长为半径作圆。再以线段垂直平分线的交点为圆心，作一样大的圆；连接端点和两圆交点，就得30°的角（如图3所示）。

师：很好，这是一个创新之举。下面讲的是老师的作法，其实和第二个同学的思路不谋而合，都想到构造等边三角形去解决问题（如图4、图5、图6所示）。

图6展示的是直角的三等分，那么任意角可以进行三等分吗？对于这样一个问题的回答我们就要再次翻开数学历史一角。介绍尺规作图中的三大不可作问题。

【设计意图】

通过求作一个角等于30°，想通过转化到另一类特殊角60°或90°去完成，第一主要是熟练作图技能；第二是展示“转化”在解决问题中的重要性。

【教后反思】

在教学过程中，教师边听边画图记录，和其他学生一起去理解该学生的作图想法，在这个教与学的过程中，出彩的不是教师而是学生。因此，有时不要以为班中没有思维好的学生，而是因为我们没有给予好的问题。教学过程中学生并不会全部按照教师的预设展开思考，当师生思维不同路时，出彩也就在不同的路上。

问题二：求作点P（，0）。

生：（1）连接（0，1）和（2，0）两个点；（2）以点O为圆心、该线段长为半径作弧交x轴的正半轴于点P，即为所求点P（，0）。

师：是无理数，无理数是一个无限不循环小数。用尺规作图的方法可以“抓住”这一类无理数。同样我们继续思考下面的问题：若记点（0，1）为A，点（2，0）为B，则请你在两坐标轴上求作点Q，使△ABQ为等腰三角形。

生：以点A为圆心、AB长为半径作圆，再以点B为圆心、AB长为半径作圆，与x、y轴的交点即为所求的点Q。

师：满足条件的点还有吗？

生：过两圆的交点作一条直线l，与x、y轴的交点也是所求的点Q。

师：找到了几个点Q？

生：x、y轴上各有四个点，一共可作出8个Q点（如图7）。

师：能不能把这条直线l对应的函数关系式求出来……

【设计意图】

一是利用圆规旋转截等长线段构点，积累直观操作经验；二是让学生再次利用尺规作图理解无理数与数轴上的点的对应关系；三是引申出已知点与一次函数图像的关系，在复习中多一点知识之间的串联。

【教后反思】

当学生说出“过两圆的交点作一条直线，与x、y轴的交点也是所求的点Q。”我心里一阵惊喜，没想到学生给出了如此简单直接的说法，究其原因，第一种可能是这名学生对于图形中的对称现象观察非常到位；第二种可能是这名学生对垂直平分线的画法理解透彻，可以说这就是我们要寻找的“几何直观”思维，预设虽好，但是生成更好。

三、教学启示

日本东京大学大学院教育学研究科教授、教育学博士佐藤学在《教师的挑战——宁静的课堂革命》一书中提到：“在教学中教师的中心工作在于倾听、串联、反刍。可以说，串联是教学的核心。”

1.倾听与态度。

在教学的过程中，如果不去认真倾听问题一中的两名学生的作图叙述，不去听从学生的指令动手画草图，那肯定捕获不到教学的有效生成，或许生成会变为生而不成，学生的创新思维也就不会被大家所见。因此作为授课教师需要准备好的问题，也需要准备倾听学生回答的态度。随时随地捕捉到学生在课内课外的声音，善于发现学生心灵之美、思维之美，并给予学生更多的鼓励和赞美，是教师的一份深深的教学情怀。若当聆听到学生给出的答案不够正确时，我们可以听一下培养学习型组织倡导者彼得·圣吉说的话：婴儿学走路，是在跌倒、爬起、再跌倒、再爬起的过程中学会的。学生思维能力的发展就像婴儿学走路一样，要经过一个想错、再想、再错、再想的过程。学生的每一个错误都意味着成长，教师要有“祝贺失败”的修养。

2.串联与丰富。

知识之间可以串联，思维方法之间可以串联，学科之间可以串联，课内与课外也可以串联，特别是在移动互联网下校内和校外的学习更是可以串联。通过串联使得复习课不仅仅再现几个知识点，再练几道习题，而是能在复习的过程中呈现出更为丰富的学习资源。例如本节课中由三等分直角引出尺规作图中的三大不可作问题，即任意角三等分、立方倍积、化圆为方，从中让学生感知数学中也有不能解决的问题，但即使“不能”也需要给出证明，感知“几何作图”可以转化为“代数运算”解决。课堂上通过将数学文化和数学教学串联起来，为学生展示数学的另一面。同时串联将原先分散学到的知识点、解决问题的方法连点成片实现学习效能提升，让数学学习变得更厚实、更丰富。因此串联应成为教师自觉的教学追求。

3.预设与生成。

教学中需要预设，预设是对将要学习的问题、面对授课学生的知识能力、水平作提前研究和准备，但预设并不是教学的全部，生成伴随其左右。例如图3的图形该学生设计的作图有相当大的思维量，完全是一种个人思维的成功，在这个环节里不要讨论，不要提示，只需学生动手动脑，教师做的就是等待“生成”，生成出的新思维一定超出教师的预设。因此数学复习课中要以数学问题为主，以激发学生思维为核心，多为学生创设问题单和思考空间，让学生在变换的环境中加以应用，实现数学思维和解决问题能力的提升，在这样的复习教学中预设精彩，生成出彩。

总之，数学复习课，尤其是非毕业班的复习课应少一点应试的功利，多一点思维的空间，增一点数学文化的营养。只有这样复习课的品质才能有所提升。

【参考文献】

[1]周建勋.无锡市中考尺规作图的命制及思考[J].中学数学月刊，2014（11）.

[2]赵齐猛.挖掘教材的数学文化价值——从Koch曲线谈起[J].中学数学，2014（24）.