经历过程的体验教学与反思

[摘  要] 文章阐述了“正方体截面形状”这节体验教学课的过程，并对其进行了总结与反思. 这节体验教学课遵循“四个理解”，引导学生在“做”中体验，关注学习过程，层层深入，从操作层面的直观经验到理性层面的逻辑思考，采用了技术和实物工具相结合的方式，把主动权交给学生，做到了“以生为本”. 体验式教学能让学生体验知识的发生与发展过程，能提升学生的空间想象能力和逻辑思维能力，能促进学生数学素养的提升.

[关键词] 学具;操作;过程;体验

《义务教育数学课程标准（2022年版）》[1]指出，除接受学习外，动手实践、自主探索与合作交流同样是学习数学的重要方式. 学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程;数学教学应让学生亲身经历将实际问题抽象成数学模型，并进行解释和应用的过程，进而使学生获得数学知识的同时，在思维能力、情感态度与价值观等方面也得到提高与发展.

数学课程标准的实施，要求数学教学不仅要关注结果，更要重视学习过程，让学生亲身经历知识的发生和发展过程. 下面结合2021年6月笔者开设的“正方体截面形状”一课，谈谈笔者在教学中的一些体验和感受，恳请读者不吝赐教.

教学流程及设计意图

1. 创设情境，激发兴趣

教学时，笔者引入切割钻石的视频——切割工匠们通过画线和标记，把粗糙的原石切割成不同多面体的钻石，切割后的钻石熠熠生辉，光彩夺目，价值也很高. 可是，如果原石切割不好，会直接影响其价值.

师：如果老师手里有一块原石，你们想通过切割把它变成美丽的钻石吗？

生（齐）：想！

设计意图数学源于生活，生活中处处有数学. 从生活实例出发，用图文并茂、生动形象的微视频创设情境，比采用单一的教学手段进行教学更具有吸引力和感染力. 观看原石经过切割变成钻石的过程，不仅能让学生感受到切割的重要性和科学性，还能激发学生的好奇心和求知欲，为这节课的学习奠定基础.

2. 层层递进，经历过程

师：为了探索这个实际问题，今天我们聚焦截面形状的问题，按照从特殊到一般的研究思路，我们先来看看切割正方体的截面问题. 首先，请大家大胆猜想一下，如果每个同学都有一块正方体原石，要求只切割一刀，你们觉得切割面会是什么形状？

生1：如果切去正方体的一个角，切割面会是一个三角形;如果竖着切或者横着切，切割面会是一个长方形或一个正方形，其他的我不太确定.

师：生1想到了切割面可能是三角形、长方形或者正方形，其他同学呢？

生2：我也觉得不太好说，因为它不是平面的.

师：既然说不清楚，那我们该怎么办呢？

生3：我觉得可以画出一个正方体，然后进行切割.

师：同学们都画画看吧！（教师巡视）

师：看来画图不能解决问题，那我们接下来该怎么办呢？

生4：如果有一个真正的正方体拿来切割就好了.

师：老师现在給每组一个正方体积木，你们试试看.

（学生拿到积木后开始观察、思考，小组交流、研讨）

生5：老师，我觉得可以切割成一个梯形（生5展示切割的方法，如图1所示）.

生6：也可以切割成一个菱形和一个（普通的）平行四边形（生6展示切割的方法，如图2和图3所示）.

师（追问）：切割面还会是什么形状？

（学生沉默）

设计意图通过“想图形”，学生很难想象正方体切割面的形状，大多数学生感觉很困难. 当教师追问时，学生想到“画图形”，画一个正方体，但是画在纸上的正方体是平面图形，如果学生的空间想象能力不足，感受正方体截面的所有形状还是有困难. 接着，给出正方体“实物”，可是学生没法把正方体积木切割开，只能通过在表面画线的方式进行想象. 学生在这种情况下发现了截面可以为梯形、菱形、平行四边形. 显然，只靠观察实物得到正方体其他切割面的形状，对学生来说还是挺困难的，这恰恰说明了用正方体学具解决切割面形状问题的必要性. 可见，没有经历过程，没有真正的体验，要想象出所有正方体截面的形状是很困难的.

3. 借助学具，深刻体验

笔者这时才从盒子里拿出里面装有蓝色液体的透明正方体学具——“水立方”（两种型号，液体体积占比为10%、40%的正方体分别称为“1号水立方”和“2号水立方”，如图4所示）. 笔者把“水立方”发给每一组的学生，他们拿到后便开始动手操作. 在操作的过程中，很多学生发现了不同的截面形状. 笔者借助希沃技术，把学生的操作演示给大家看，然后让学生把要切割的线在正方体积木的表面画出来.

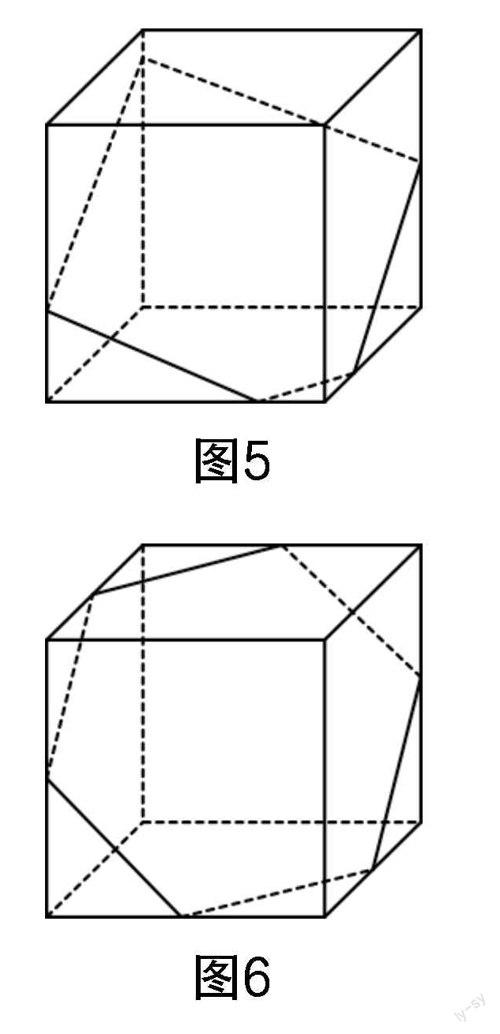
学生用“水立方”操作，除了发现截面形状有三角形、长方形、正方形、平行四边形、梯形、菱形外，还用2号水立方发现了截面形状还有五边形和六边形，如图5和图6所示.

4. 启思明理，层层深入

师：大家观察一下，截面的每1条边是怎样产生的？

生7：每1条边都是水面和正方体的面相交产生的.

师：正方体的截面的形状最多是几边形呢？

生8：最多是六边形，因为正方体一共有6个面，水面和每个面相交，最多产生6条边.

师：当截面的形状是三角形时，会产生哪些特殊的三角形？

生9：等腰三角形和等边三角形.

师：截面的形状会是直角三角形吗？请说明理由.

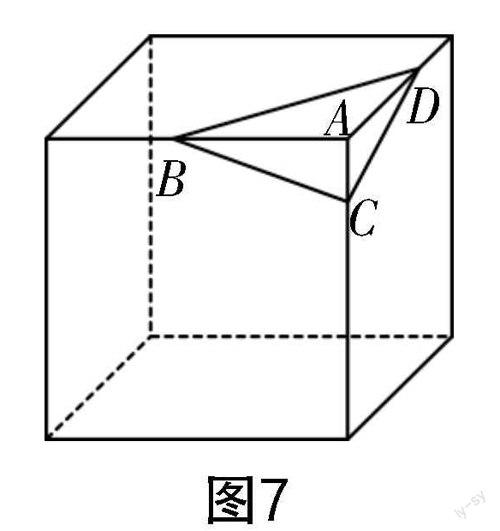
生10：如图7所示，假设截面△BCD是直角三角形，且BD是最长的边. 因为BC2=BA2+AC2，DC2=AD2+AC2，所以BC2+DC2=BA2+AC2+AD2+AC2=BA2+AD2+2AC2. 因为BD2=BA2+AD2，所以BC2+DC2>BD2. 所以截面△BCD不是直角三角形.

师：非常好！那么，当截面的形状是四边形时，这些四边形的边有什么共同特征？

生11：我们得到的截面的形状有矩形、菱形、梯形、正方形、平行四边形，这些图形至少有一组边是平行的，这一组平行的边应该是正方体相对的2个面与水面相交形成的.

师：很好！大家再想一下，截面的形状是五边形和六边形时，会有几组平行的边？

生12：当截面的形状是五边形时，5条边是水面和正方体的5个面相交形成的，所以应该有2组平行的边;当截面的形状是六边形时，6条边是水面和正方体的6个面相交形成的，应该有3组平行的边.

师：回答得非常好！现在老师想问大家，如果原石的形状是三棱锥，那么，切一刀，截面会有哪些形状？

生13：因为三棱锥共4个面，所以截面会出现三角形或四边形.

设计意图“水立方”学具为学生直观地观察截面形状提供了方便. 学生在操作“水立方”的过程中得到了所有正方体截面的形状，并且能深层次地思考出截面的形状不可能是七边形、直角三角形，正方体相对的两个面与水面相交形成的边是平行的. 学生由学习正方体截面形状积累的经验，得到了截三棱锥所形成的截面的形状是三角形或四边形这一结论，发展了思维.

教学反思

课后，笔者根据专家提出的宝贵意见和给出的中肯建议，以及数学教材中出现的一些类似教学体验环节，对这节课进行了深刻的反思.

1. 理解数学

物理和化学都是实验性学科，与它们相比，数学目前的教学现状是很少有实验，甚至没有. 学生希望通过数学实验得到真正经历和体验的教学. 数学是一门思维性极强的学科，思维的形成离不开体验，借助实物工具，通过手和脑相结合的方式去体验，引发学生思考，促进学生对知识的理解和掌握，这才是真正的数学教学.

本节课以“做”为支架，引领学生经历过程，手脑并用，充分体验，启思明理，借助学具帮助学生更直观地理解知识，通过操作体验和思考其中的原理，真正推动了数学课堂学习方式和教学方法的变革.

2. 理解教学[2]

教学主要是根据学生的最近发展区，为学生搭建适合学生的“脚手架”，让学生真正理解知识，做到灵活运用. 学生比较容易接受具体、直观、形象的事物，所以教师在教学中要引领学生从特殊到一般，从具体到抽象，从简单到复杂，逐渐深入. 教学要让学生通过“做”数学，手脑协同，启思明理，经历完整的数学学习过程，要让学生不仅知道知识从哪里来，还知道知识往哪里去. 同时，教学要为学生的数学学习提供资源，比如提供教学所需要的教具、学具等，给学生带来学习方式的创新.

本节课，笔者设计的“脚手架”一层一层逐级上升，从“想图形”，到“画图形”，再到“看实物”，最后到使用学具，学生的思维层次在不断加深，逻辑思维能力也在逐渐提升. 本节课能让学生全身心地参与课堂、动手操作，真正地做到了经历每一个过程，充分体验并理解了截面每一个形状的产生过程.

不过，本节课的教学超时2分钟，原因是学生受传统教学方式的影响较深，通过实验来体验学习的教学方式，学生还不是很适应.

3. 理解学生

笔者上课的学生是八年级的学生，他们具有一定的推理能力. 在动手操作环节，学生通过体验，去感悟，去发现，去归纳，去总结，经历了知识的形成和发展过程，真正地理解了知识，课堂教学目标达成得较好. 这样的课堂，学生喜欢，所以数学课堂要以生为本，要处处为学生着想，要真正理解学生.

本节课，笔者把主动权留给学生，让学生一步步思考. 当学生遇到困难时，笔者并没有立即把学具拿出来，而是一步一步地引领学生去思考、去推理. 且课堂上笔者所提的问题，均由学生通过操作体验、独立思考和交流探讨来解决.

4. 理解技术

本节课是实物和信息技术的有机结合课，微视频的引入、希沃技术的展示和“水立方”学具的体验，这些技术和实物工具的使用，激发了学生的学习热情，尤其是“水立方”学具，其功能和作用在这节课中发挥得淋漓尽致. 随着时代的发展和技术的更新，学生的学习方式和教师的教学方式都在发生变化.

《义务教育数学课程标准（2022年版）》提出，要结合学生的认知特点，遵循学生数学核心素养发展的需要，将多媒体、授课软件等信息技术融入教学. 把信息技术应用在课堂中，不仅能促进学生数学学习能力的提高，还能促进教师教学水平的提升. 学具直观、生动，具有化抽象为形象、化静态为动态、化结果为过程的优点，学具的使用能帮助学生理解数学、发现数学、验证数学，能调动学生通过多种感官去体验，去启思明理，促进学生高效学习. 目前，数学教学还有很多教学内容需要学具，所以学具的制作和创新、使用和推广，已经成为教师日常教学备课的常态.

回顾体验[3]

笔者还是学生时，班里有一个空间想象能力不足的学生，她一直都想不明白正方体的截面形状为什么会有五边形和六边形. 为了研究正方体的截面形状，她曾在学校买过很多橡皮，在家又拿豆腐块做过实验，把它们做成正方体，用小刀去截……如果她能上这节课，亲身感受“水立方”学具，相信她一定会立刻顿悟.

笔者作为父亲，曾经给1岁多的女儿讲“桌子上的水太热，不能摸”，她不是很理解. 有一次，她的手被热水烫了，从这次经历中，她体验并深刻地理解了“热的东西不能摸，会烫手”.

笔者初为教师时，曾为备好一节课，不断地试讲、总结、寻找原因，去听一些名师的课，学习教学方法，获取教学的真谛;也曾因为学生不理解知识而闷闷不乐. 后来，笔者经历了近10年的教学磨炼，体验了每节课的收获与困惑后逐渐明白，教师应找准学生思维的最近发展区，从生活中寻找教学素材，深挖教材，从学生的角度去思考，精心设计每节课，让学生经历知识的获取过程，体验教学的“酸甜苦辣”.

回顾这节课，在笔者循序渐进的引导下，学生经历了从“想图形”“画图形”“看实物”到学具演示的过程，积累了从操作层面的直观经验到理性层面的逻辑思考的经验. 这节课将操作与思维有机地融为一体，使得抽象的知识变得具体，复杂的问题变得简单，表象的问题变得深刻，学生不仅“知其然”，更“知其所以然”.

回顾这节课，通过教学活动，学生感受到了使用学具的必要性. 在操作的过程中，学生的数学思维逐渐深入，不仅培养了学生的动手能力、空间想象能力和逻辑思维能力，还激发了学生对数学活动的兴趣，促进了学生真正地理解和掌握知识，他们的数学素养也得到了提升.

回顾这节课，要让学生经历数学知识的产生和发展过程，需要教师为学生搭建促使其参与课堂的平台，要让学生主动地去操作、去思考、去發现、去经历探索过程，只有经历了、体验了，对知识的理解才会更透彻. 在操作中体验、经历探索过程，有利于激发学生的探究兴趣，能培养学生的研究热情，有利于学生调动多种感官进行有效学习，有利于学生创新思维和实践能力的培养，有利于学生思维的生长和数学素养的提升，同时有利于教师对课程资源进行深度挖掘，从而提升教学水平.

参考文献：

[1]中华人民共和国教育部. 义务教育数学课程标准（2022年版）[M]. 北京：北京师范大学出版社，2022.

[2]黄玉华. 画其图  变其形  明其理  探其用[J]. 中学数学杂志，2019（04）：19-23.

[3]万涛. “折等腰三角形”体验活动的实践与思考[J]. 中学数学杂志，2021（06）：16-19.