3-PRS并联机构的动力学惯量耦合特性分析*
2021-08-06倪仕全田大鹏
倪仕全,田大鹏*
(1.中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033;2.中国科学院大学,北京 100049)
0 引 言
并联机构具有高刚度、高精度、良好的动态性能、易于实现高速度等优点,在天线支撑、轮毂打磨、医疗器械等方面得到了广泛应用[1-5]。并联机构是一个多入多出非线性系统,目前,对其研究主要集中于运动学、动力学等方面。然而机构的驱动支链存在动力学惯量耦合现象,这种现象在机构高速、高加速运动中更加明显,严重影响了并联机构的动态性能[6]44[7]604。研究并联机构的惯量耦合特性对提升机构的动态性能具有重要意义。
由于并联机构耦合方面的研究主要集中于运动耦合、刚柔耦合等,对于刚度大、高速运动的并联机构,惯量耦合引起的动力学耦合现象更严重[8-10]。文献[11]对Stewart并联机构提出了惯量耦合特性的分析方法。文献[12,13]分析了Stewart并联机构惯量矩阵具有对角占优及机构关节间具有惯量耦合的特性。文献[14]研究了Stewart并联机构在关节空间中负载与电机惯量配比关系。文献[15]提出了3-PRS并联机构惯量耦合特性的分析方法,但没有针对动平台位姿耦合的关系进行解耦。文献[16]提出了Stewart并联机构的耦合惯量特性评价指标,并给出了指标在工作空间的分布规律。文献[17]针对CrossⅣ并联机构,提出了支链间耦合作用的等效惯量参数计算方法。
上述研究中缺乏统一描述惯量耦合特性的标度。文献[7]605研究了2(3HUS+S)并联机构在关节空间中的惯量耦合特性,并提出了降低主动支链间动力学耦合强度的措施;文献[6]50针对5 PSS/UPU并联机构提出了惯量耦合特性指标,并给出了指标在机构工作空间中的分布规律。
笔者在已有研究的基础上,在充分考虑并联机构惯量矩阵为对角优势阵、惯量耦合特性统一标度的情况下,定义惯量耦合特性;首先,对3-PRS并联机构进行运动学分析,针对动平台广义位姿、速度、加速度存在耦合的问题,进行解耦;采用虚功原理建立机构的动力学模型,基于此,建立机构在关节空间的动力学模型,最后对机构进行惯量耦合特性分析。
1 3-PRS并联机构运动学分析
1.1 3-PRS并联机构描述
3-PRS并联机构结构简图如图1所示。
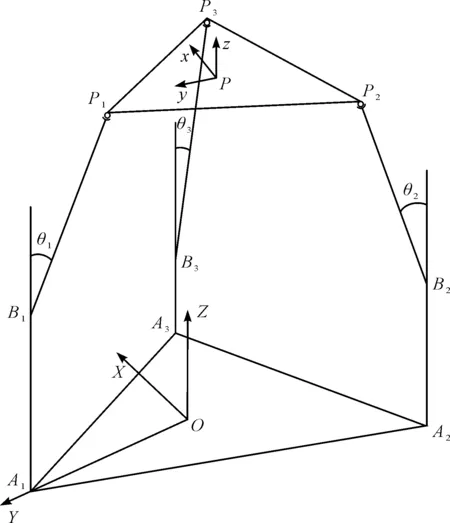
图1 3-PRS并联机构Bi(i=1,2,3)—包括沿导轨运动的移动副、连接滑块与从动件的转动副;Pi—球面副;θi—导轨与从动件的夹角
该机构由静平台、动平台及3条相同支链构成。每条支链按移动副—转动副—球面副的顺序依次连接静平台与动平台,移动副处滑块的导轨垂直固定于静平台。3条支链限制了机构的运动特征,使动平台具有3个自由度:两个转动、一个移动。
机构尺寸参数:静平台外接圆半径为R,动平台外接圆半径为r,从动件长度为l。
1.2 机构逆运动学建模
图1中,笔者在静平台上建立静坐标系O-XYZ,原点位于平台几何中心;Y轴沿OA1方向并与之共线,Y轴与OAi之间夹角为αi;Z轴垂直于静平台方向向上,根据右手定则确定X轴;OAi垂直于对应的转动副轴线。
动坐标系P-xyz的建立过程与坐标系O-XYZ相同,其中:
(1)
动平台绕O-XYZ的X轴、Y轴、Z轴分别转动角度为α、β、γ,则动平台相对静平台的旋转矩阵为:
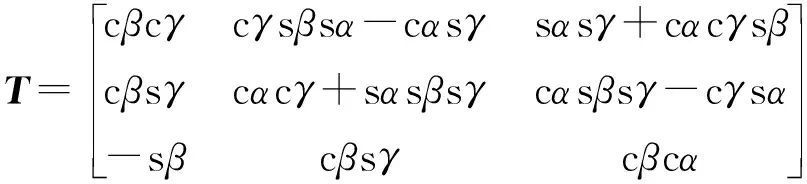
(2)
式中:sαi—sinαi;cαi—cosαi。
由文献[18]可得机构伴随运动为:
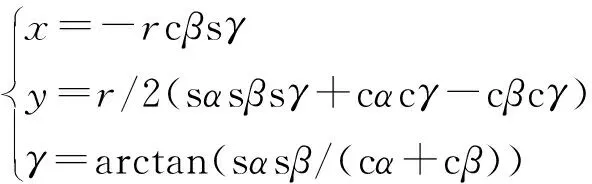
(3)
联立式(1~3),并根据杆长l不变的条件,可得机构的运动学逆解为:
(4)
式中:PiX—点Pi在静坐标系X轴坐标;PiY—点Pi在静坐标系Y轴坐标;PiZ—点Pi在静坐标系Z轴坐标。
1.3 移动副速度、加速度映射分析
动平台各球面副中心点Pi的速度为:
vpi=v+w×pi=JpiV
(5)
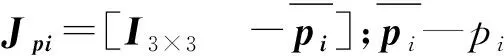
动平台各球面副中心点Pi的速度还可以表示为:
vpi=vbie+wli×li
(6)
式中:vbi—移动副速度;wli—从动件角速度。
由式(5,6)可得移动副速度:
vbi=JbiV
(7)
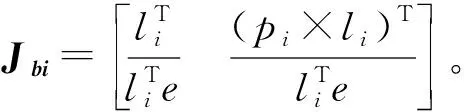
式(7)可改写成矩阵形式为:
vb=JbV
(8)

(9)
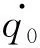
α、β、γ对α、β、z求偏导,即:
(10)
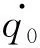
联立式(9,10)可得:
(11)
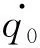
由式(8,11)可得机构的解耦速度雅可比矩阵为:
(12)
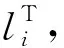
(13)
式中:εli—从动件角加速度。
式(13)可改写成:
abi=JbiA+VTJiV
(14)
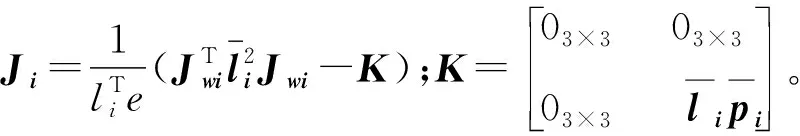
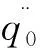
(15)
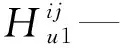
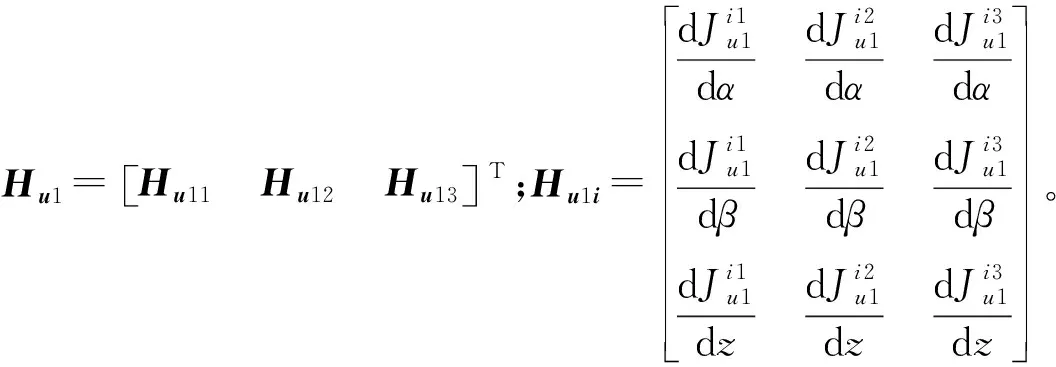
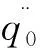
(16)

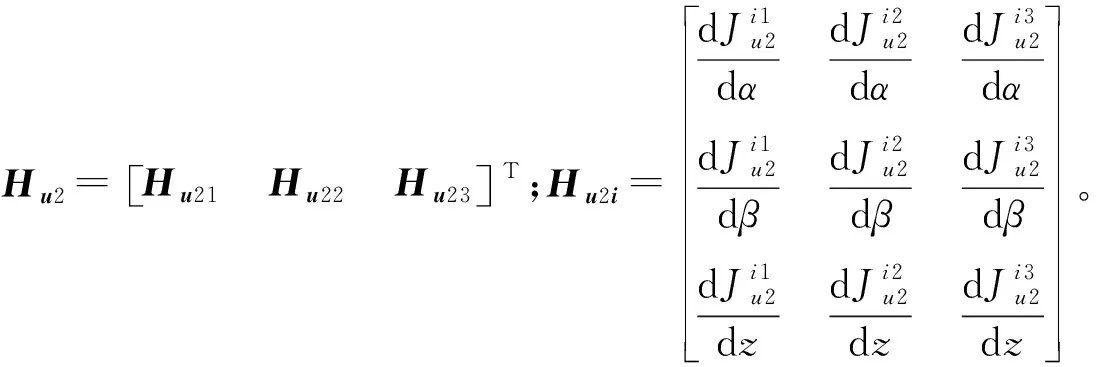
由式(15,16)可得:
(17)
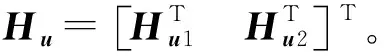
式(14)可表示为:
(18)
1.4 从动件速度、加速度分析
1.4.1 从动件速度分析
(19)
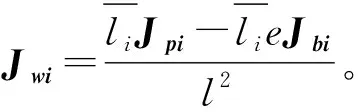
从动件质心处速度为:
(20)
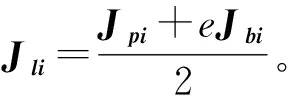
1.4.2 从动件加速度分析
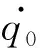
(21)
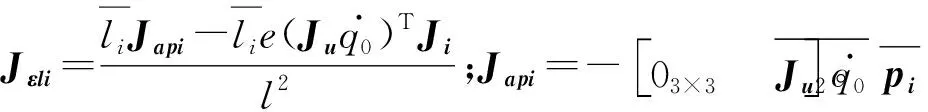
对式(20)求导,可得:
(22)
1.5 运动学仿真
验证机构运动学分析的正确性,需将仿真结果与理论计算值进行对比[20]。
机构尺寸参数如下:R=0.055 m;r=0.035 36 m;l=0.040 m。
令动平台的中点轨迹如下式:
(23)
由式(4,7,18)可得到机构3个滑块理论位移、速度、加速度,如图2所示。
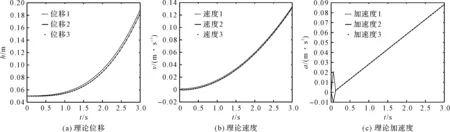
图2 滑块理论位移、速度、加速度
笔者在运动学仿真软件Simulink/SimMechanics工具箱中,建立机构的三维模型,得到机构3个滑块的位移、速度、加速度,如图3所示。
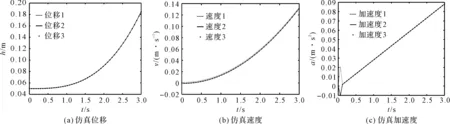
图3 滑块的仿真位移、速度、加速度
在图3(c)中,初始时刻,滑块的加速度出现跳变,这是由于动平台在式(23)的初始位姿与机构初始位姿不同造成的。从图2和图3可看出:该结果验证了机构运动学建模、动平台位姿(速度、加速度)解耦的正确性。
2 3-PRS并联机构动力学分析
2.1 受力分析
在不考虑运动副存在摩擦力的情况下,笔者对各个构件的受力进行分析,建立机构的动力学模型。
滑块受力为:
(24)
式中:τi—驱动力;mb—滑块质量;g—重力加速度向量。
从动件受力为:
(25)
式中:ml—从动件质量;Ili—从动件在静坐标系的惯量矩阵。
动平台受力为:
(26)
式中:fe—外力;ne—外力矩;mp—动平台质量;Ip—动平台在静坐标系的惯量矩阵。
2.2 3-PRS并联机构整体动力学建模
对于3-PRS并联机构而言,主动力为各杆件的惯性力(矩)、重力、驱动力、外力(矩)。根据虚功原理,机构主动力做的虚功之和为零,即:
Wh+Wl+Wp+Wf=0
(27)
式中:Wh—滑块主动力所做虚功;Wl—从动件主动力所做虚功;Wp—动平台主动力所做虚功;Wf—外力(矩)所做虚功。
由式(24~27)可得机构的动力学方程:
(28)
式中:M—惯量矩阵项;C—向心力及科氏力项;G—重力项。
2.3 动力学数值算例
2.3.1 并联机构的参数定义
机构的静平台、动平台及从动件的尺寸参数值同1.5部分,并联结构的其他参数值如表1所示。
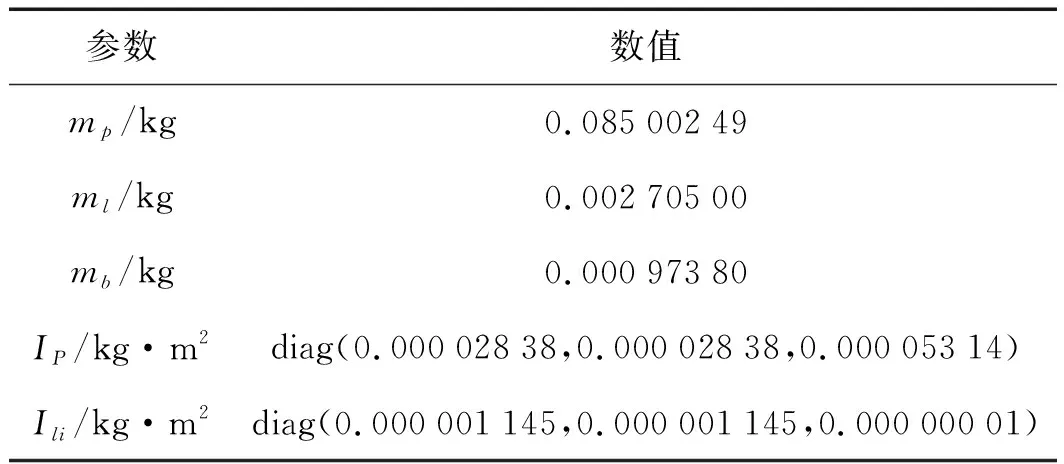
表1 结构参数
2.3.2 算例计算
在不考虑动平台受到外力(矩)扰动的情况下,此处令动平台的位姿变化轨迹为:
(29)
3个支链的理论驱动力及仿真驱动力如图4所示。
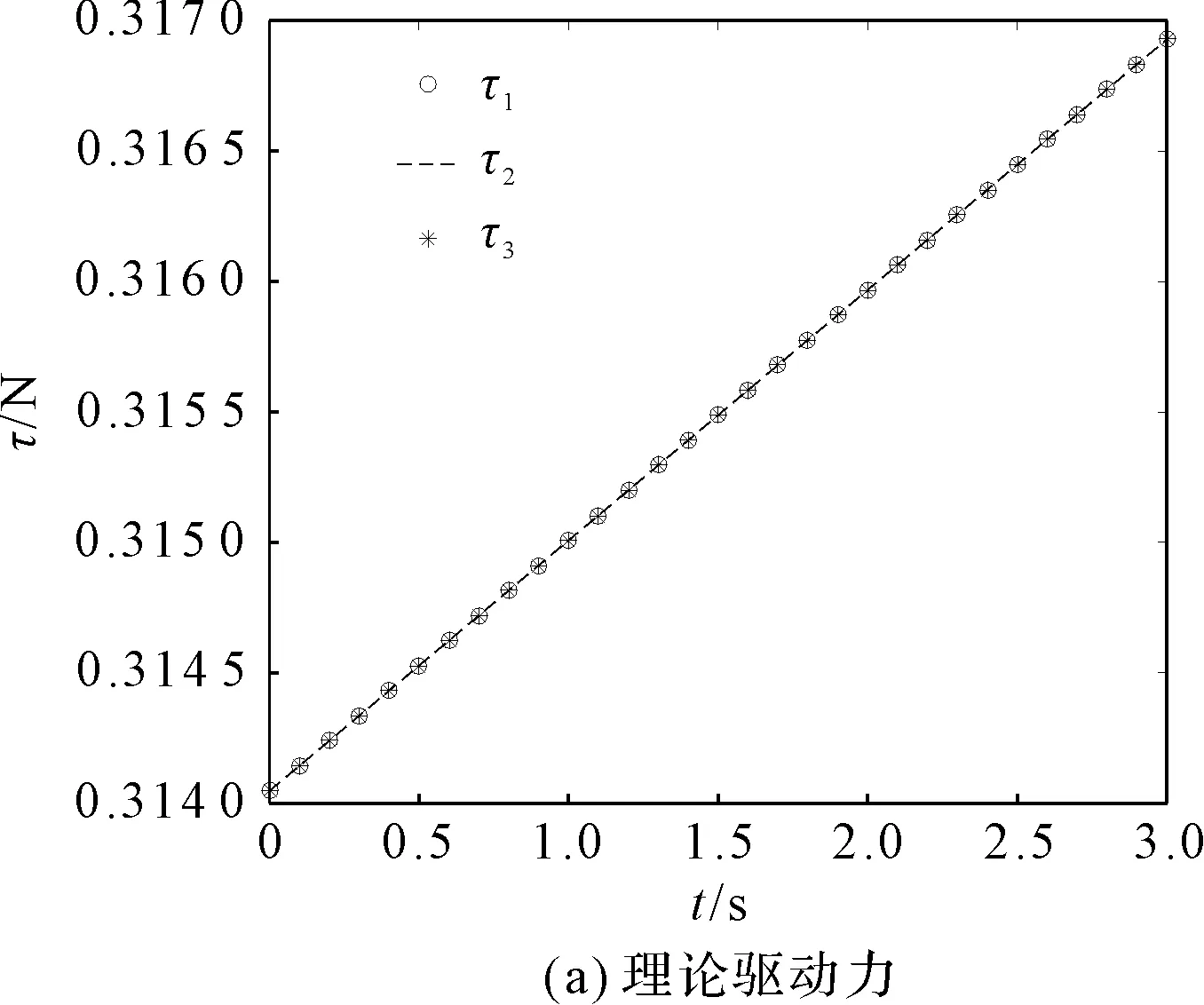
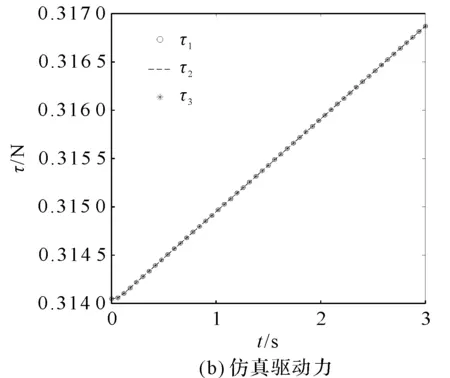
图4 支链的理论驱动力及仿真驱动力
从图4可知:理论驱动力、仿真驱动力曲线完全吻合,验证了动力学建模的正确性。
3 3-PRS并联机构惯量耦合特性分析
3.1 关节空间动力学模型的建立
根据机构在广义坐标和关节空间坐标下动能相等的原理,可得:
(30)
式中:Mg—关节空间下的惯量矩阵。
当机构在运动过程无奇异情况时:
Mg=(J-1)TMJ-1
(31)
对式(12)求导可得:
(32)
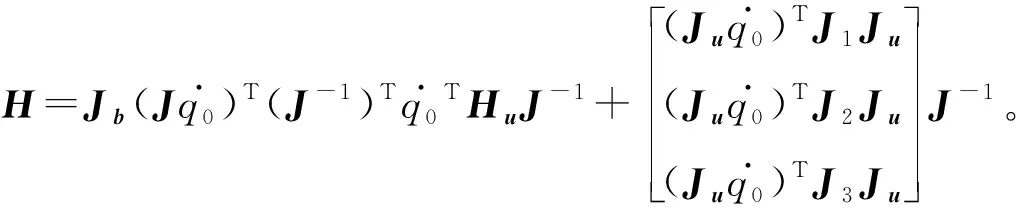
则并联机构在关节空间坐标的动力学方程为:
Mgab+Cgvb+Gg=τ
(33)
式中:Cg—关节空间下的向心力及科氏力项,Cg=(J-1)T(-MJ-1H+CJ-1);Gg—关节空间下的重力项,Gg=(J-1)TG。
3.2 惯量耦合特性评价指标
由式(33)可知,各通道的力和运动矢量存在着复杂的耦合关系,即一个输入影响多个输出,同时一个输出受多个输入的影响。
则本研究将评价指标值定义在(0,1)之间,这便于直接反应机构惯量耦合强度;指标值越大,耦合越大,反之越小。
此处定义惯量耦合特性ICIi为:
(34)
且需满足下式的条件:
(35)
同时,需求雅可比矩阵行列式值来判断机构是否存在奇异位姿。
3.3 仿真实验及结果分析
根据惯量耦合特性评价指标,笔者对3-PRS并联机构耦合特性进行数值仿真分析。根据机构的各条件约束及其可工作空间,选取机构位姿运动范围为:α∈[-10°,10°]、β∈[-10°,10°]、z∈[-24 mm,24 mm]。
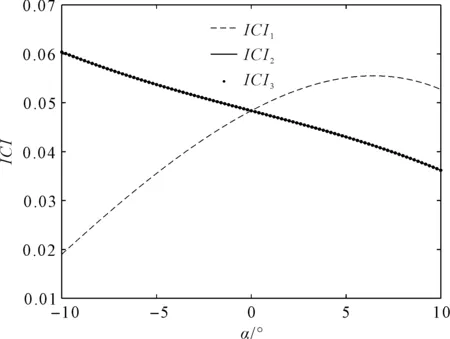
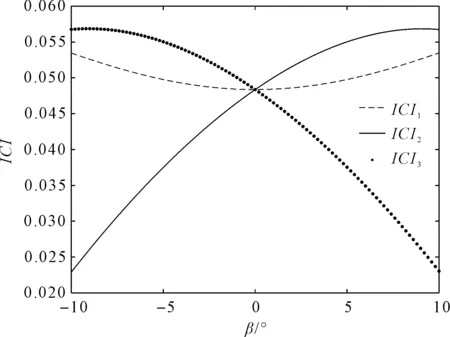
当α=0,β=0时,动平台沿Z轴在运动范围移动时,0.025 图5 惯量耦合特性随z方向分布规律 图5中:3个支链的惯量耦合特性强度随z变化一致,且变化范围较大;随着z值的增大,惯量耦合强度先减小后增大;在-7.2 mm处,惯量耦合强度最小;各ICI最小值分别为:ICI1=9.964×10-4;ICI2=1.005×10-3;ICI3=1.004×10-3;在z轴运动范围最大数值处,支链间的惯量耦合强度最大。 当β=0,动平台中心点z值处于初始状态时,动平台绕O-XYZ转动时,0.031 图6 惯量耦合特性随α方向分布规律 图6中:支链2、3的耦合惯量随α的变化一致,且变化范围较小;支链1的耦合惯量随着α数值增大先小后增大且变化范围较大。 当α=0,动平台中心点z值处于初始状态时,动平台绕O-XYZ转动时,0.031 图7 惯量耦合特性随β方向分布规律 图7中:支链2、3的耦合惯量随β的变化相反,这是因为支链2、3关于Y轴对称,且耦合惯量变化范围较大;支链1的耦合惯量随着α数值增大先小后增大且变化范围较小。 针对动平台广义位姿、速度、速度存在耦合的问题,笔者通过机构约束方程、影响系数矩阵对其进行了解耦,建立了支链与动平台末端的映射关系,验证了解耦及解耦后运动学模型的正确性;基于虚功原理,笔者建立了3-PRS并联机构的动力学模型,通过仿真软件验证了模型的正确性;在关节空间中建立了机构的动力学模型,分析了机构支链间的惯量耦合特性。 研究结果表明:在并联机构可工作空间内,通过合理规划机构各个参数的运动范围,可在一定程度上减小主动支链间的耦合惯量,来提高并联机构的动态性能,但是不能从根本上消除。 在以后研究中,笔者将会基于并联机构惯量耦合特性的特点,将其应用于并联机构的具体设计研究当中。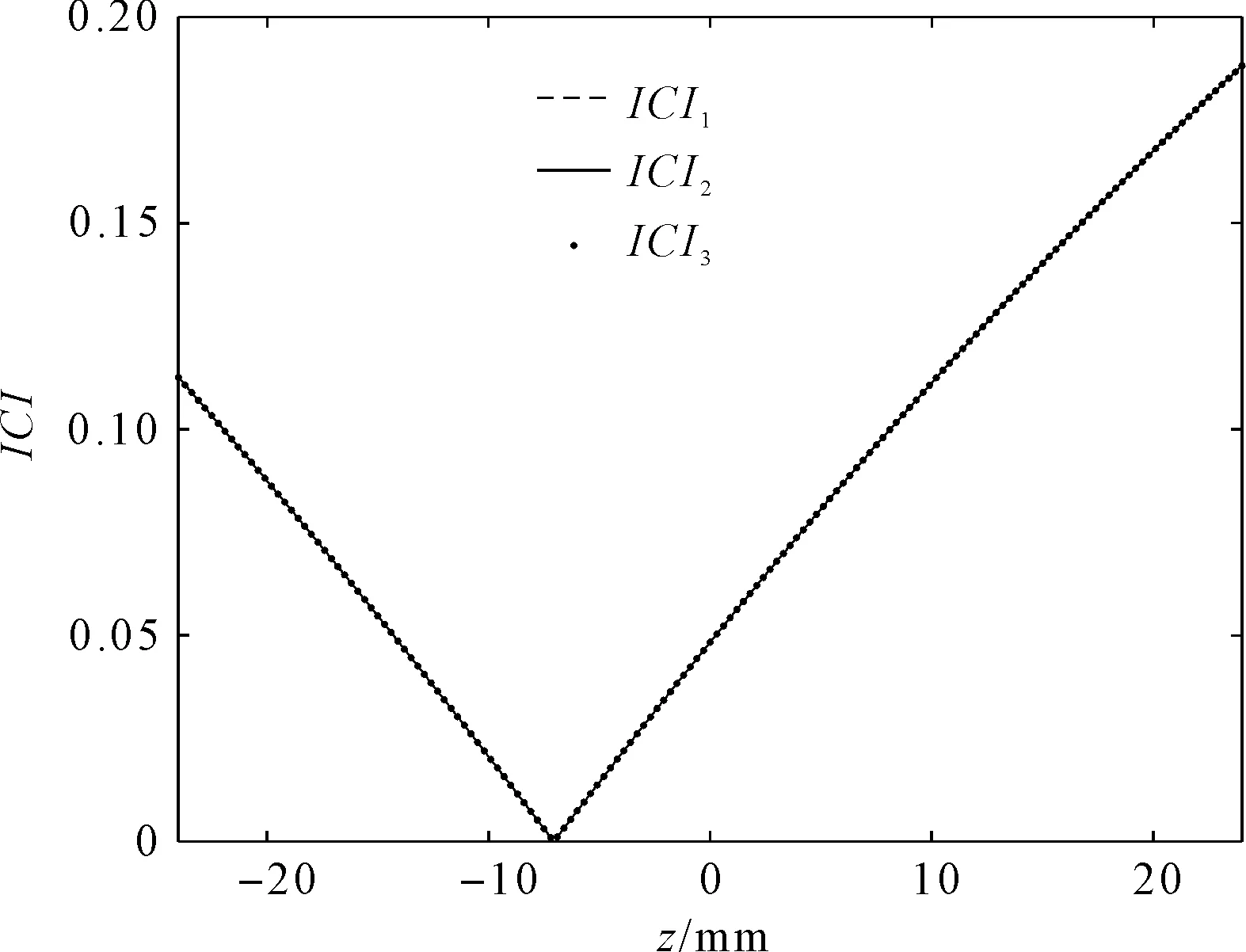
4 结束语
