封装设备中偏心轮机构的运动分析与仿真

郝术壮，孙玮淇，庞苏娟

(北京中电科电子装备有限公司，北京100176)

偏心轮机构是将旋转运动转换为直线运动的重要实现方式。其结构简单，加工方便，因此，在许多后封装设备中都有所应用，如排片机摆臂竖向运动和粘片机顶针顶起机构。不足之处是实现旋转转换为直线运动时，主动件与从动件的运动规律呈复杂函数关系，这对控制有所不利，特别是要求从动件满足某种运动规律，比如精确的直线定位、S 形加减速控制，则应用起来有很大困难。但是，如果掌握其运动规律，并配以伺服电机驱动，偏心轮机构可以实现复杂精确的运动形式。

本文将从理论和仿真两个方面对偏心轮凸轮机构进行分析。在进行理论分析时，分别推导了尖顶从动件和平顶从动件与主动件旋转角度、速度、加速度之间的运动规律。这将为伺服电机运动控制实现从动件规划运动规律奠定基础。为方便对偏心轮机构在不同起始位置对从动件运动产生的影响，文中将运用ADAMS 软件对偏心轮机构的运动进行仿真。ADAMS 软件是MSC 公司的一款多体动力学仿真软件，用其建立模型后，能够方便地完成运动学和动力学计算[1]。不仅在实现各种初始条件的计算中带来便利，还可以验证理论推导的正确与否。仿真时，对主动件设置不同初始旋转角度，可以得到从动件不同的运动特性。对各个运动曲线进行对比分析，找到最佳起始位置，方便机械设计时参考。

1 偏心轮凸轮理论运动规律

偏心轮机构是一种凸轮机构，根据从动件与主动件接触的形式，可分为尖顶从动件偏心轮凸轮机构和平顶从动件偏心轮机构[2]。尖顶从动件偏心凸轮机构的主、从动件间的接触点的位置始终相对从动件固定，而平顶从动件偏心轮凸轮机构的主、从动件间的接触点的位置相对从动件来回变化。正因如此，导致两种形式的偏心凸轮机构有不一样的运动规律。下面将分别推导。

图1是某型号排片机上的偏心轮凸轮机构，该偏心凸轮机构可以简化为尖顶从动件偏心圆盘凸轮机构，如图2所示。

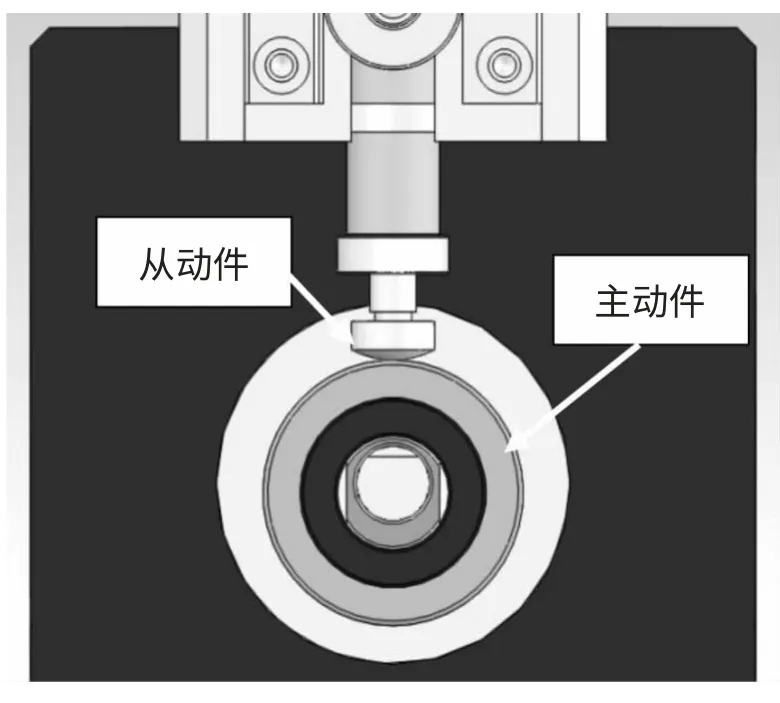
图1 某型排片机上的偏心轮凸轮机构

图2 尖顶从动件偏心圆盘凸轮机构简图

当偏心轮从起始位置A 转至B 点从动件上升位移：

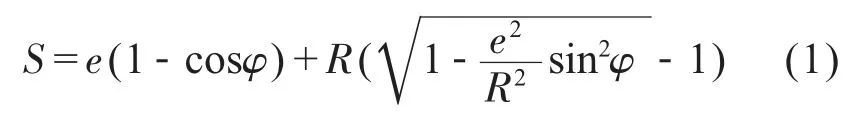
上升速度：

上升加速度：

从以上三式可以看出，尖顶从动件偏心轮凸轮机构的运动规律不是完全的余弦曲线变化规律。略去上述各式中后一项，仅保留第一项，可得到平顶从动件偏心轮凸轮机构的运动规律。如图3所示，当偏心轮从起始位置A 转至B 点从动件上升位移：

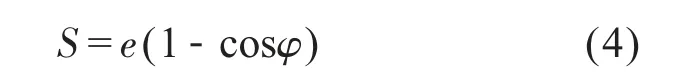
上升速度：

上升加速度：

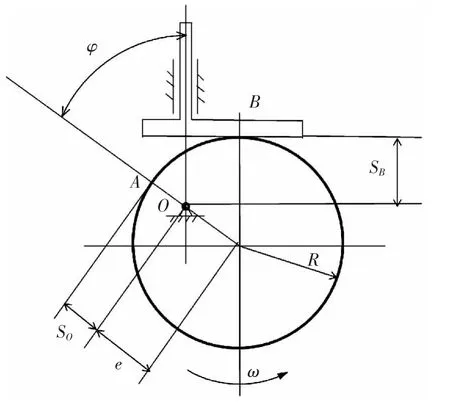
图3 平顶从动件偏心圆盘凸轮机构

以下是尖顶从动件偏心轮凸轮机构与平顶从动件偏心轮凸轮机构运动规律对比曲线：

由式(1)、(2)、(3)可以看出位移、速度、加速度的差值大小与偏心轮半径、偏心距的大小有关，减小偏心距或加大轮半径都可以使差值减少，从而使更接近余弦加速度运动[4]。当尖顶从动件偏心轮凸轮机构与平顶从动件偏心轮凸轮机构运动规律相差不大，可以将尖顶从动件偏心轮凸轮机构的运动规律简化为式(4)、(5)、(6)表示。将其与等速螺旋线凸轮的运动规律相比较，如图7所示。

图4 从动件位移随主动件角度变化曲线

图5 从动件速度随主动件角度变化曲线

图6 从动件加速度随主动件角度变化曲线

对比分析知，在40°～140°之间，偏心轮与等速螺旋线凸轮的位移差值小于10%；在60°～120°之间，偏心轮与等速螺旋线凸轮的位移差值小于2.3%。

图7 偏心轮凸轮与等速螺旋线凸轮运动比较

2 偏心轮凸轮机构ADAMS 仿真

在ADAMS 中建立尖顶偏心轮仿真模型。为方便分析和显示清晰，模型中只保留了轮轴、主动件和从动件，如图8所示。

理论上，凸轮按完整的余弦运动时，应只有柔性冲击，但当仅利用其余弦曲线的一部分时则会产生刚性冲击。这个过程可以通过在ADAMS 仿真看出。在所建立的凸轮模型中设定不同的初始角度，便可得到从动件在不同初始角下的运动规律。在ADAMS 中设置不同初始角的方法就是在图9所示对话框中的Displacement IC 处设定不同的值。不同初始角度时偏心轮凸轮机构从动件加速度变化情况如图10所示。

图8 尖顶偏心轮仿真模型

图9 初值设置对话框

图10 不同初始角度时偏心轮凸轮机构从动件加速度

对比分析所得到的各运动规律曲线可以看出，从动件的确有不同大小的冲击。初始角在0～90°，随初始角度逐渐增大，机构从动件初始时刻的加速度变化越大，相应的冲击也就越大。初始角在90°～180°，随初始角度逐渐增大，机构从动件初始时刻的加速度变化逐渐减小，相应的冲击也减小。

3 结 论

通过前文的分析和仿真可以得到以下几点结论：

a)尖顶偏心轮凸轮机构的运动曲线不是余弦曲线，平顶偏心轮凸轮机构的运动曲线才是余弦曲线。减小偏心距或加大轮半径都可以使差值减少，尖顶偏心轮凸轮机构运动曲线接近余弦运动。当尖顶从动件偏心轮凸轮机构与平顶从动件偏心轮凸轮机构运动规律相差不大，可以将尖顶从动件偏心轮凸轮机构的运动规律简化为余弦运动。

b)将偏心轮凸轮机构与等速螺旋线凸轮机构对比知，转角在40°～140°之间，偏心轮与等速螺旋线凸轮的位移差值小于10%；转角在60°～120°之间，偏心轮与等速螺旋线凸轮的位移差值小于2.3%。

c)当凸轮按完整的余弦曲线运动时，只有柔性冲击，但当其仅利用余弦曲线的一部分时会有刚性冲击。其冲击程度随初始角度的变化而变化。初始角在0～90°，随初始角度逐渐增大，机构从动件初始时刻的加速度变化越大，相应的冲击也就越大。初始角在90°～180°，随初始角度逐渐增大，机构从动件初始时刻的加速度变化逐渐减小，相应的冲击也减小。

综上可知，在应用偏心轮凸轮机构时，最好让其按完整的余弦曲线运动，否则会产生刚性冲击。由于偏心轮凸轮机构从动件的运动与凸轮转角之间的关系是接近余弦或余弦的，因此其关系是非线性的，对于控制调节十分不利。如果应用偏心轮凸轮机构做从动件精确定位运动，为减小控制难度，可以使其工作在60°～120°之间。但这样，有效行程就大打折扣，可用查表的方法，进行从动件高度控制，即在程序中将不同的从动件高度与凸轮转角之间关系做出表格，当需要改变高度时，让程序查表即可。

[1]陈立平，张云清，任卫群，等.机械系统动力学分析及ADAMS 应用教程[M].北京：清华大学出版社，2005.

[2]濮良贵，纪名刚.机械设计（第8 版）[M].北京：高等教育出版社，2006.

[3]哈尔滨工业大学理论力学教研室.理论力学（第7 版）[M].北京：高等教育出版社，2009.

[4]纪志明，何在洲，廖仁文.偏心圆凸轮机构的运动学和动力学分析[J].军械工程学院学报.1998，9(2)：68-71