纯滚动条件下滚动轴承滚球自转速度的计算*

2021-08-06祁宏伟牛蔺楷谢宏浩郑一珍熊晓燕

机电工程 2021年7期

关键词：滚球套圈内圈

祁宏伟,牛蔺楷,2*,谢宏浩,肖飞,郑一珍,熊晓燕,2

(1.太原理工大学机械与运载工程学院,山西太原 030000;2.太原理工大学新型传感器与智能控制教育部重点实验室,山西太原 030000)

0 引言

滚动轴承是现代机械装备的关键核心部件之一,因此,如果滚动轴承发生故障,将严重威胁设备的安全可靠运行。目前,已有许多学者对滚动轴承的故障诊断展开了广泛而深入的研究。

在滚动轴承的故障诊断分析和动力学分析中,滚动体沿着自身轴线的旋转速度(即自转速度ωb)是计算滚球故障特征频率(ball defect frequency, BDF)和滑滚比的重要参数[1,2]。

对于外圈固定,内圈旋转的滚动轴承而言,在纯滚动条件下,HARRIS T A的经典著作[3]中给出了滚球自转速度的计算方法。为了便于后续讨论,本文将文献中给出的自转速度表示为ωbH。

在对滚动轴承进行故障诊断的研究中,ωbH是提取滚动体故障特征的重要参数。对于ωbH在滚动轴承故障诊断中的应用,文献[4-7]已经进行了详细的讨论。在动力学分析中,ωbH广泛地应用在对故障轴承的动力学建模和振动响应分析中[8]。MISHRA C等人[9]采用键图法,提出了一种考虑滚动体故障的球轴承动力学模型。SAWALHI N等人[10,11]在考虑了滚动体故障的情况下,建立了轴承-齿轮系统的动力学模型。在MISHRA和SAWALHI的模型中,ωbH被用来确定滚动体缺陷与套圈发生碰撞的时刻。据此,CHOUDHURY A等人[12]采用集中质量法建立了含滚动体故障的滚动轴承转子系统动力学模型。在文献[12]中,ωbH被用来确定由于滚动体故障而产生周期冲击的时间间隔。WANG H等人[13]建立了考虑滚动体表面波纹度的球轴承动力学模型,ωbH被用来确定在特定时刻时滚动体波纹度的幅度。

虽然ωbH广泛地应用于故障诊断和动力学分析中,但笔者通过研究发现,ωbH并不能给出纯滚动条件下滚球自转速度的合理值,主要原因在于得出ωbH的推导过程中,忽略了滚球中心点的平移速度对其自转速度的影响。

为此,本文首先从运动学角度出发,对计算ωb的合理公式进行推导;进而,本文构建含有滚球缺陷的球轴承动力学模型,通过研究冲击之间的时间间隔对所提方法在计算滚动体自转速度方面的合理性进行讨论。

1 运动学分析

首先给出ωbH的计算公式为:

(1)

式中:ωi—内圈旋转速度;D—滚动体直径;dm—轴承节径;α—接触角。

为了深入说明式(1)在计算滚球自转速度时存在的问题,本节首先对式(1)的推导过程进行简要的说明,进而在此基础上提出本文的计算方法。需要说明的是,此处对于式(1)的推导仅从运动学角度展开,不涉及离心力、陀螺力矩等复杂的动力学问题。

1.1 推导过程及其存在的问题

球轴承在yz平面和xz平面的几何参数如图1所示。

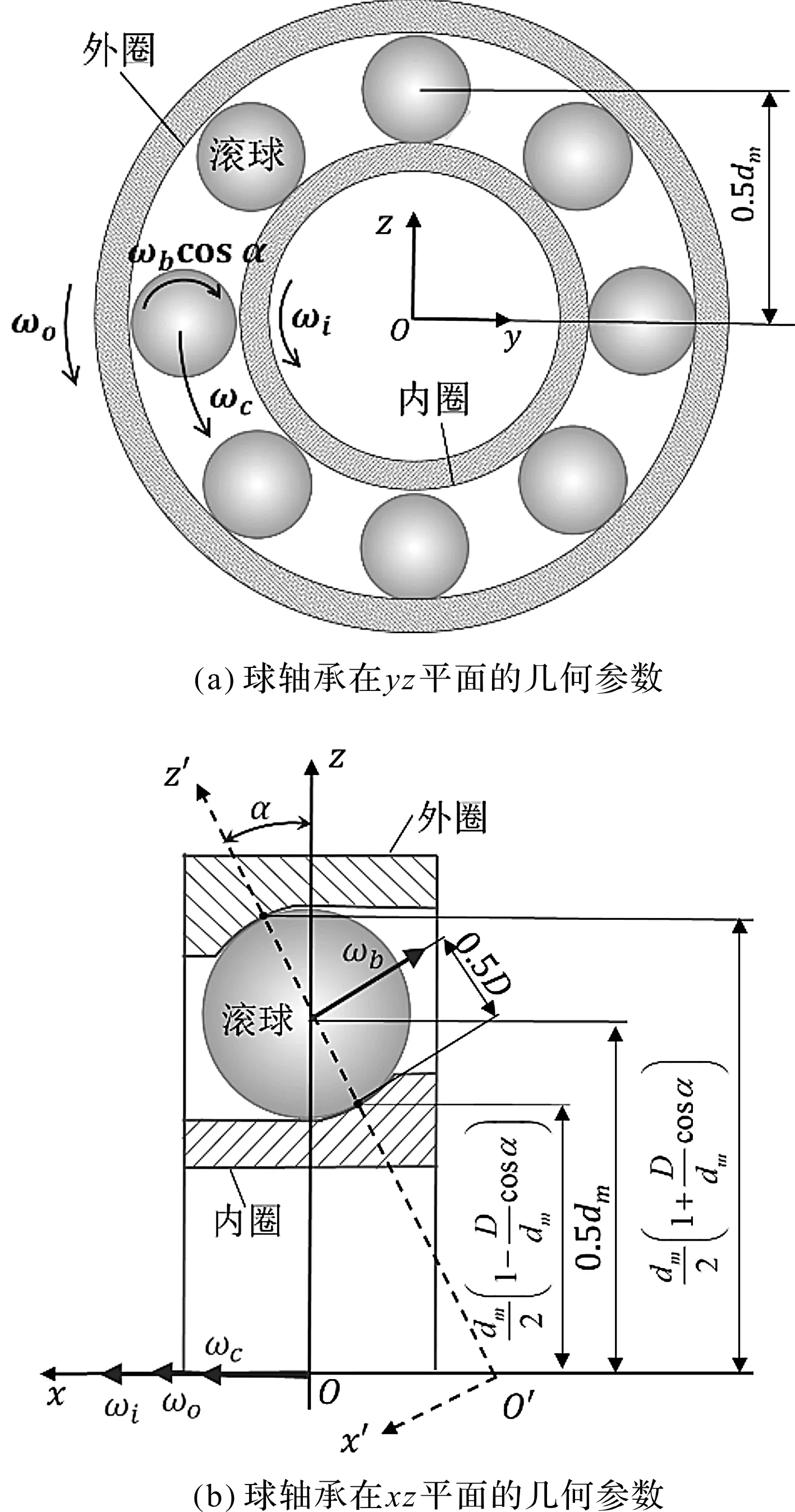
图1 球轴承在yz平面和xz平面的几何参数坐标系Oxyz—惯性坐标系,x轴—轴承的旋转轴线;坐标系O′x′y′z′—接触坐标系,z′轴通过接触点,z′轴和z轴的夹角即为接触角α;ωo—外圈转速;ωi—内圈转速;ωb—滚球自转速度(ωb在yz平面的投影即为ωbcosα);ωc—滚球的公转速度(保持架转速);各转速以逆时针方向为正方向

为了分析方便,笔者将轴承的外圈固定(即图1中ωo=0),内圈和保持架绕轴承轴线旋转的角速度分别为ωi和ωc。因此,内圈相对于保持架的旋转速度为ωi-ωc。

在对滚球进行分析时,Harris分析框架下的滚球自转速度计算如图2所示。

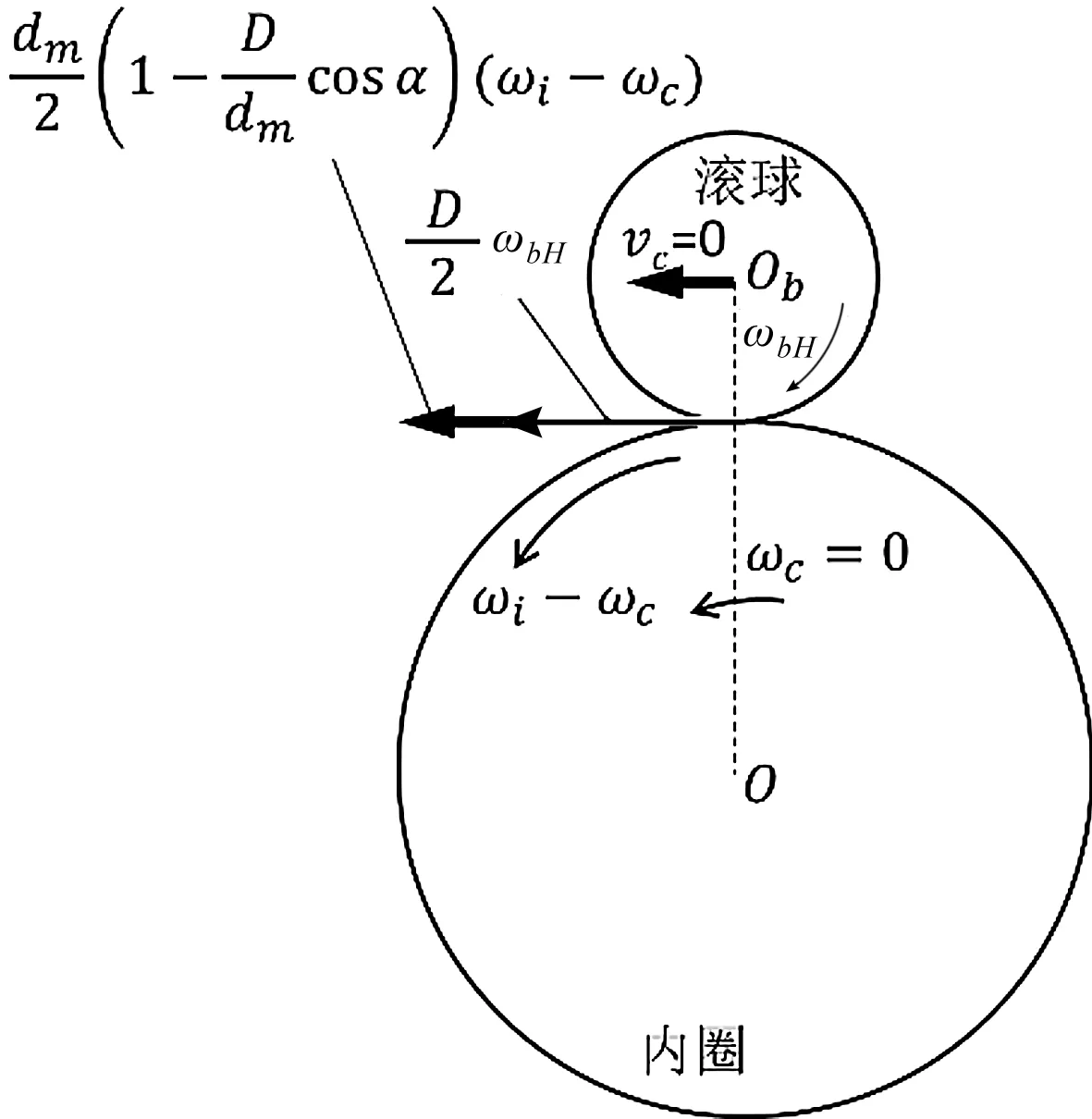
图2 纯滚动条件下计算滚球自转速度(Harris分析框架)

令保持架的转速ωc=0(ωc=0意味着滚球中心Ob和内圈中心O的连线OOb绕轴承中心的旋转速度为0),则内圈按照ωi-ωc进行旋转。当ωc=0时,滚球中心的平移速度vc也相应变为0。

在保持架转速ωc=0的分析框架内,内圈在接触点处的速度为:

(2)

滚球在接触点处的速度为:

(3)

当忽略接触点处于相对滑动的情况下(即纯滚动条件下),滚球在接触点的速度等于内圈在接触点的速度(vibH=vbiH),即:

(4)

由式(4)可以得到:

(5)

由文献[3]46-51可知,保持架转速ωc可以表示为:

(6)

最终,将式(6)代入式(5)中,即可得到式(1)。

通过上述对ωbH推导过程的讨论可以看出,滚球在接触点的速度对自转速度的计算具有重要的影响。实际上,当滚球表面点按照滚球自转速度绕滚球轴线旋转的同时,滚球中心会同时绕着轴承中心进行公转,公转速度即为ωc。因此,根据速度合成定理,滚球表面点速度应该为滚球自转速度ωb和公转速度ωc共同作用的结果。然而,式(3)和式(5)在建立时仅仅考虑了滚球自转速度对滚球接触点速度的影响,导致式(1)也未能充分考虑滚球公转速度对表面点速度的影响。因此,ωbH无法合理表征自转速度。

需要说明的是,虽然式(1)无法合理表达自转速度,但可以对滚球故障特征频率进行合理的计算(其原因在第2节进行详细的说明)。

1.2 计算ωb的合理方法

在纯滚动条件下,滚球自转速度的计算(本文分析框架)如图3所示。

图3 纯滚动条件下计算滚球自转速度(本文分析框架)

(7)

内圈在接触点的速度可以表示为:

(8)

在纯滚动条件下,vib=vbi,即有:

(9)

对式(9)进行整理,最终有:

(10)

由以上讨论可以看出,与式(5)相比,本文所推导的自转速度表达式,即式(10),考虑了滚球中心速度对滚球接触点速度的影响,因此可以得到更为合理的自转速度。

进而,对比式(5)和式(10),有:

ωb=ωbH-ωccosα

(11)

2 动力学分析

本节通过动力学分析进一步验证本文在1.2节中所提计算方法的合理性(即在计算滚球自转速度时需要考虑滚球接触点的平移速度)。

在动力学分析中,轴承元件旋转速度通过对动力学方程进行数值积分后得到。为了建立其动力学方程,需要计算其相对滑动速度,以得到轴承元件的摩擦力和力矩;计算滑动速度则需要计算接触点的平移速度。由此可以看出,当采用不同的计算方法计算接触点平移速度时,会得到不同的自转速度。

由第1节的相关分析可知,式(1)的建立不考虑滚球中心速度对接触点平移速度的影响,而本文建立式(10)时,考虑了滚球中心速度对接触点平移速度的影响。在动力学分析时,如果在考虑滚球中心速度对接触点平移速度的影响的情况下,得到更为合理的结果,则可以说明本文所提方法的合理性。

为了对自转速度进行分析,笔者建立了一个能够考虑滚球局部损伤的动力学模型。

滚球损伤的示意图如图4所示。

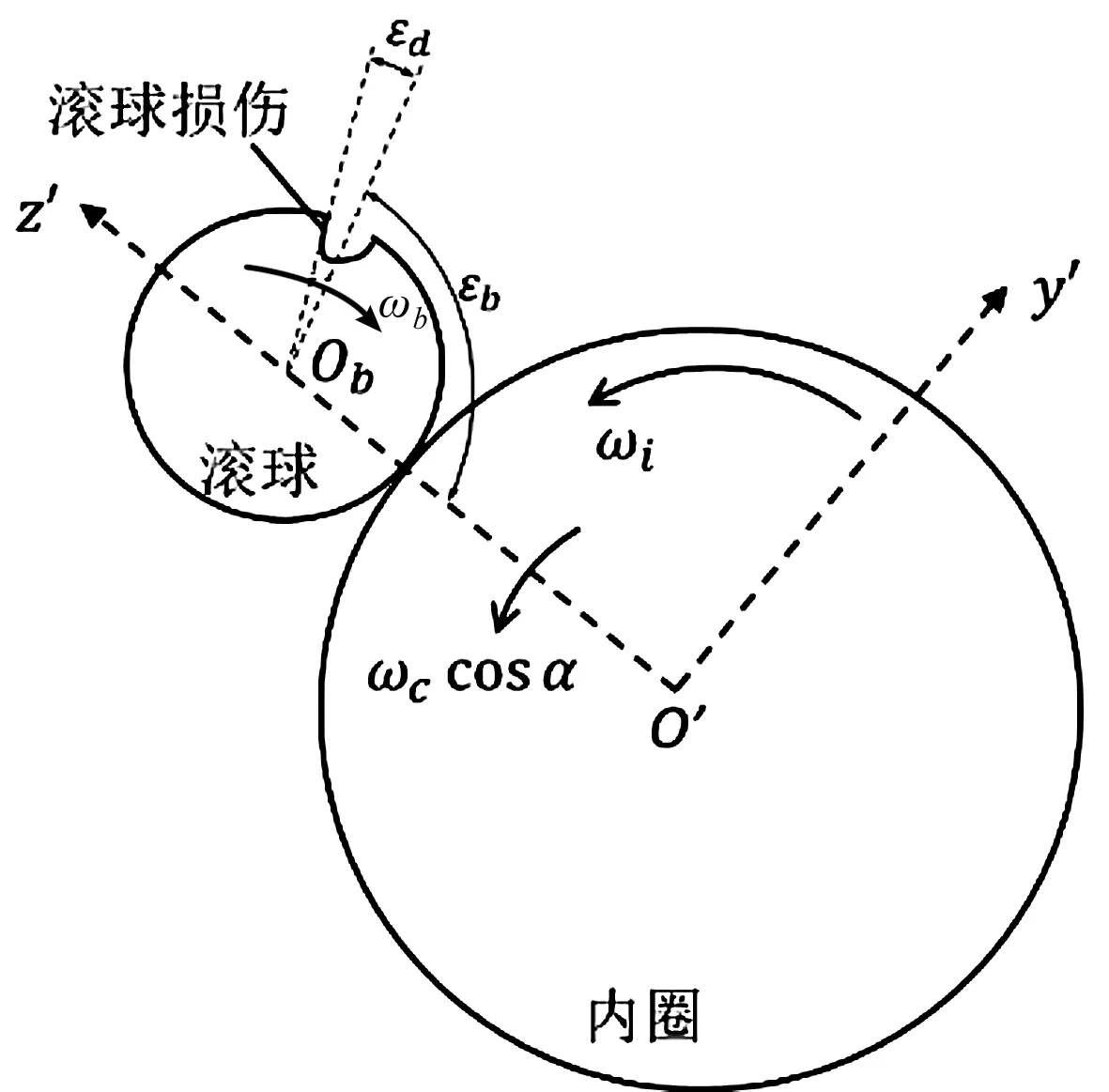
图4 滚球局部损伤

图4中,当滚球自转时,滚动体损伤会周期性地和套圈发生碰撞,并产生一系列冲击,每一个冲击之间的时间间隔与滚球自转速度具有直接的关系。因此,可以通过对冲击时间间隔的研究,来对滚球自转速度进行一定的分析。

当滚球损伤通过连线ObO′时,该损伤就会与套圈发生碰撞并产生一定的冲击。因此,BDF对应的就是损伤连续通过连线ObO′(对同一个套圈)的时间间隔。在滚动体损伤以ωb的角速度绕滚球中心旋转时,连线ObO′也同时以速度ωccosα绕着轴承中心进行旋转。也就是说,BDF受到角速度ωb和ωccosα的共同影响,即|ωb|+|ωccosα|。由于ωbH比ωb大ωccosα,ωbH可以计算得到合理的BDF。

为了建立能够考虑滚球损伤的动力学模型,笔者首先建立正常轴承的动力学模型,并基于损伤的产生,对轴承几何和动力学特性的影响建立损伤模型;然后将损伤模型与正常动力学模型进行模型融合,最后得到考虑了滚球损伤的动力学模型。

此处笔者使用的正常轴承动力学模型基于由Gupta开发的ADORE(advanced dynamics of rolling elements)模型构建。模型ADORE能够对轴承内部各元件(滚动体、套圈、保持架)以及各元件之间复杂的时变动力学行为进行模拟。

关于ADORE中详细的建模过程可参见文献[14-16]。本节仅对ADORE的基本建模过程进行必要的讨论。

ADORE中计算旋转速度的流程如图5所示。

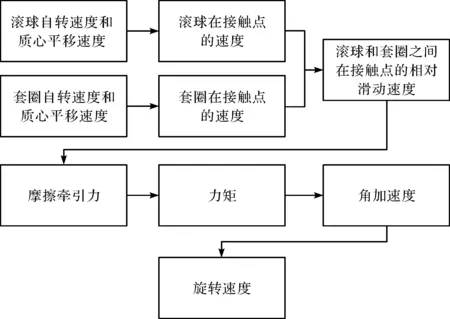
图5 ADORE中计算旋转速度的流程

以球和套圈相互作用为例。首先,笔者根据球中心的平移速度和球的旋转速度,来确定球和套圈在接触点的速度;由球和套圈在接触点的速度之差,计算它们在接触点的相对滑动速度。当得到相对滑动速度后,将相对滑动速度代入一定的润滑剂牵引模型,就可以得到其摩擦力。摩擦力将决定作用在轴承元件上的力矩。当力矩确定后,可根据欧拉方程计算角加速度。然后,通过对角加速度进行数值积分,从而计算出下一时刻轴承元件的转速。

由以上讨论可知,轴承元件接触点处的速度直接影响着两个元件的相对滑动速度,并进一步影响着球的旋转角速度。如上面所述,通过式(5)和式(10)计算得到的不同结果,原因在于滚球在接触点的平移速度计算方法的不同。

2.1 相对滑动速度的计算

2.1.1 基于本文所提方法

在动力学模型中,基于本文在1.2节中提出的方法(滚动体接触点平移速度应为滚球自转速度和滚球中心平移速度共同作用的结果),滚球和内圈在接触点处的速度可以分别表示为:

ui=vi+ωi×ri

(12)

ub=vb+ωb×rb

(13)

式中:ωi,ωb—内圈和滚球的自转速度矢量;ri,rb—内圈和滚球在接触点相对于内圈中心和滚球中心的位置矢量;vi—内圈中心的平移速度矢量;vb—滚球中心的平移速度矢量。

在惯性柱坐标下,可将vb写为:

(14)

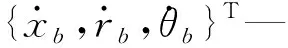
则:滚球和内圈在接触点处的相对滑移速度为ui-ub。

2.1.2 基于式(1)的推导方法

基于式(1)的推导方法,内圈和滚球在接触点的速度可以分别写为:

(15)

(16)

则:滚球和内圈在接触点处的相对滑移速度为uiH-ubH。

从上面的讨论可以看出,基于本文所提方法和式(1)的推导方法,可以得到两种滑动速度的计算方法。如果基于滑动速度ui-ub计算得到的冲击时间间隔是合理的,则说明本文所提出的计算滚球自转速度的方法是合理的。

2.2 滚球局部损伤模型

由于材料的缺失,局部损伤对轴承各元件之间的几何趋近量会产生重要影响。

当滚球损伤与套圈发生相互作用时,二者之间的几何趋近量可以写为:

Δ=|rbc|-fD-hd如果εd≤εb

(17)

式中:hd—损伤深度;εd—损伤包容角的一半;εb—损伤中心和ObO′之间的连线(如图4所示);f—滚道沟曲率系数;rbc—滚球中心和滚道沟曲率中心之间的位置矢量。

在动力学分析中,需要实时判断两个角度的关系。如果εd>εb,则可以说明滚球损伤和滚道之间没有相互作用。

2.3 基座模型

为了研究轴承的振动,笔者在轴承外圈上增加沿轴和轴两个平移自由度,以模拟轴承箱的振动,如图6所示。

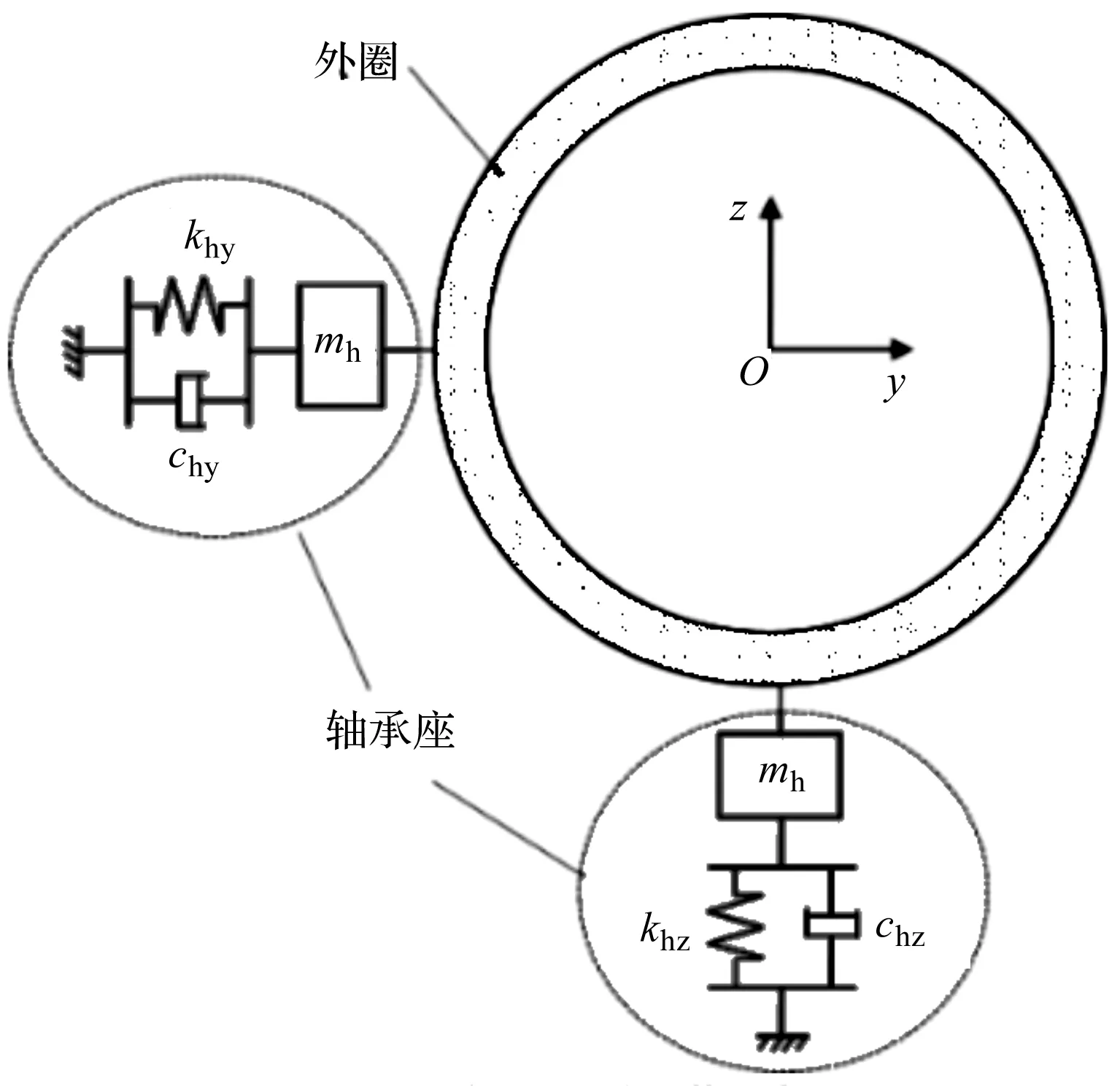
图6 轴承座模型

相应的动力学方程为:

(18)

3 动力学分析结果

笔者使用第2节中讨论的考虑滚球损伤的球轴承动力学模型,来研究当滚球损伤碰撞套圈时两个连续脉冲之间的时间间隔。

轴承的基本参数如表1所示。

表1 仿真轴承-轴承座系统参数

内圈转速为5 000 r·min-1,在内圈施加500 N的纯径向载荷。为了方便进行对比分析,本节将对比分析基于uiH-ubH和ui-ub所计算得到的结果。这两种计算方法分别称为方法1和方法2。其中,方法1与式(1)的推导相对应,方法2与本文所提公式的推导相对应。

当轴承不存在损伤,且初始接触角为0°时,由动力学仿真得到的滚球自转速度ωb如图7所示。

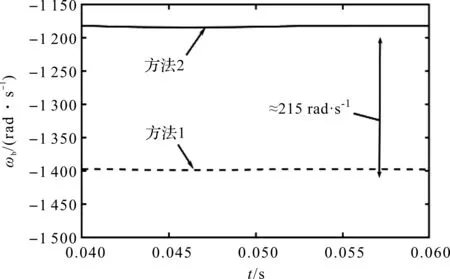
图7 动力学仿真得到的滚球自转速度

需要说明的是,图7中速度ωb的符号(“正”或“负”)基于右手法则(逆时针为正)。由于内圈转速ωi是逆时针方向的,在图7中ωb为负。当使用方法1时,结果为-1 397 rad·s-1;当使用方法2时为-1 182 rad·s-1。两者结果差为215 rad·s-1,几乎等于保持架的转速。

此外,基于方法1和2的计算得到的接触角都很小,约为0.000 12°。因此,根据方法1计算得到的球自转速度大约比按方法2计算得到的球自转速度大ωccosα,这与第2.2节的结论是一致的。

当轴承滚球含有1个深度为1 mm的局部损伤时,轴承座在z方向的加速度如图8所示。

图8 轴承座z方向的加速度

在图8中,损伤碰撞内圈时产生的冲击标为“I”,冲击外圈时产生的脉冲称为“O”。

图8(a)和图8(b)之间的一个主要区别是当滚球损伤碰撞同一套圈时,产生的脉冲之间的时间间隔。以碰撞外圈的脉冲为例。当使用方法1计算相对滑动速度时,时间间隔约为3.9 ms,对应的BDF约256.4 Hz,如图8(a)所示;当使用方法2时,时间间隔约为4.5 ms,约222.2 Hz,如图8(b)所示。

以上结果表明：当采用方法1和方法2,计算得到的滚球故障特征频率分别为256 Hz和222 Hz,两者相差约34 Hz,与ωccosα(本仿真中,α=0)相一致。

由此可以发现,当用方法2计算相对滑移速度时,BDF几乎等于用式(1)确定的BDF(由式(1)计算的BDF约为222.1 Hz)。虽然式(1)无法计算得到合理的ωb,但公式(1)已被大量实验证实可以计算得到合理的BDF。因此,根据式(7)和式(8)确定接触点速度的方法2,可用于确定实际和合理的相对滑动速度。

上述分析表明,本文所提出的式(10)计算的ωb更为合理。

此外,在不同初始接触角下,计算得到的球自转速度如表2所示。