基于FLUENT的微量润滑磨削流场仿真研究*

孙 建,钱 炜,丁子珊

(上海理工大学 机械工程学院,上海 200090)

0 引 言

随着一些前沿产业(如航空航天、军工器械、医疗器械)的快速发展,以及对产品质量要求的不断提高,高性能的元器件得到更加广泛的应用。作为材料去除过程中的最后工艺,磨削加工技术越来越受关注[1]。

在磨削过程中,极高的磨削比能会在磨削区产生大量的热,会对工件造成各种类型的热损伤,如烧伤、裂纹、相变以及不利的残余拉应力[2]。因具有成本高、冷却液利用率低、污染环境、危害工人健康等缺点[3-5],传统的浇注冷却已不能满足现代磨削加工的需求。基于绿色生产理念和降低生产成本,需要探索新的冷却方法。

MQL冷却技术是一项富有前景的技术,并有望替代传统冷却技术。该冷却技术是将微量的磨削液与压缩气体混合,形成磨削液喷雾,提高磨削液渗透到磨削区的能力,进而提高冷却效果。据已有的研究结果表明,MQL冷却技术可以有效地降低工件表面的粗糙度,减小砂轮磨损,减小磨削力,并可在一定的程度上改善工件的残余应力[6-11]。

砂轮周围的气障层是影响磨削液冷却效果的关键因素。为了提高磨削液的冷却效果,有必要对砂轮周围流场进行研究。EBBRELL S等人[12]采用实验的方式测量了砂轮的流场,其研究结果表明，在楔形磨削区会形成反射流,阻碍磨削液进入磨削区;而且其反射流会随着砂轮线速度的提高而增强,随着砂轮与工件之间间隙的减小而减弱。王春玉[13]基于计算流体力学理论,建立了三维砂轮流场仿真模型,对砂轮周围流场进行了仿真分析,其研究结果表明，砂轮与工件形成的楔形空间没有明显的返回流;而砂轮侧面流出的侧向溢流较为明显,磨削液受返回流的影响较小,会在侧向溢流作用下从侧面流出,进而降低磨削液的冷却效果。韩振鲁[14]的研究认为,砂轮轴向尺寸不会影响砂轮流场的分布;并建立了其二维仿真模型,仿真的结果显示,在楔形磨削区有明显的返回流,阻碍磨削液进入磨削区,且返回流会随着砂轮速度的提高和最小间隙的减小而增强。

MQL冷却技术较传统冷却技术更具优势,主要是因为MQL射流具有较强穿透力,更容易穿过砂轮周围的气障层到达磨削区,达到冷却润滑的目的。尽管对砂轮流场的研究和对MQL的研究有很多,但很少有学者对MQL条件下的砂轮流场进行研究;而且在砂轮流场对MQL射流进入磨削区的影响方面也少有研究。

事实上,MQL射流穿透砂轮流场的能力是决定MQL冷却效果的关键因素;而砂轮流场的分布规律对MQL射流能否进入磨削区有很大的影响。

本研究基于计算流体力学,应用FLUENT仿真软件对砂轮流场进行仿真分析,并在此基础上利用离散项仿真模型对MQL条件下的砂轮流场进行仿真分析,将磨削区的气体作为连续相,MQL雾滴作为离散相,探究微量润滑参数(气体压强、磨削液流量)对磨削液进入磨削区的有效流量的影响。

1 砂轮流场分析

1.1 砂轮流场的形成

砂轮在旋转时会带动其表面的空气微团运动,由于空气具有粘性,砂轮表面的空气微团会带动其相邻的空气微团运动,在砂轮周围形成环形气流,即圆周气流;而砂轮侧表面的空气在离心力的作用下流向砂轮边缘,新的空气不断地补充到砂轮侧面,形成由砂轮中心流向砂轮边缘的径向流;对于存在气孔的砂轮,还会形成渗透流和内部流。

因此,圆周气流、径向流、渗透流、内部流共同构成了砂轮流场[15]。

1.2 砂轮流场理论建模

在进行砂轮流场仿真时,空气的压缩性对仿真结果有着很大的影响。通常可根据空气的马赫数(Ma)来判断空气的压缩性[16-18]。

Ma计算如下:

(1)

(2)

式中:va—空气的流速;T—环境温度;a—该环境下的声速。

取环境温度T=298 K,将砂轮最大速度40 m/s代入式(1,2),可得Ma=0.115 6<0.3。由于气体动力粘度较小,砂轮周围空气流速应小于砂轮最大线速度,砂轮周围空气的马赫数(Ma)小于0.3。因此,对砂轮流场进行分析时,可将空气视为不可压缩气体。

根据流体力学理论,二维砂轮流场满足连续方程、动量守恒方程、能量守恒方程。其基本控制方程分别为:

(1)连续性方程。方程如下:

(3)

由于此处视空气为不可压缩气体,连续性方程可化简为:

(4)

(2)动量守恒方程。方程如下:

(5)

(3)能量守恒方程。方程如下:

(6)

式中:ρ—流体密度;f—体力;τ—剪切力,ui—x、y方向的速度u、v;λ—流体的导热系数;T—流场温度;cp—流体比热容;e—内能。

(4)k-ε湍流模型。

由于方程中的未知数要多于方程个数,为使方程封闭,引入k-ε湍流模型。

k方程为:

(7)

ε方程为:

(8)

(9)

式中:k—湍动能;ε—湍动耗散率;σk,σε—湍流Prandtl数;模型常量分别取值为:C1ε=1.44,C2ε=1.92,Cμ=0.09,σk=1.0,σε=1.3。

(5)二相流模型。

MQL磨削技术是将磨削液与压缩空气混合,使其雾化为微米级的液滴进而进入磨削区,以实现冷却润滑效果的润滑方法。

微量润滑中的磨削液量远远小于空气的量。在流体计算仿真中,当液体、气体体积率小于10%时,要采用离散相模型。因此,离散相模型更符合MQL射流与砂轮流场耦合场的仿真。

2 平面磨削流场仿真

2.1 几何建模与网格划分

笔者对砂轮流场进行二维仿真(仿真模型包括砂轮、工件两部分),将模型导入ICEM软件中建立二维求解域;并定义求解域边界条件,应用ICEM软件进行网格划分。

ICEM网格可分为结构网格和非结构网格。非结构网格通过定义全局网格参数,再对重要的计算区域通过局部加密的方式进行网格划分。由于砂轮与工件之间的间隙较小,采用非结构网格的方式进行划分时,在间隙附近的网格会发生严重的畸变,严重影响网格的质量,进而影响仿真结果的准确性。

而结构网格的单元网格为四边形,可以有效地避免间隙附近网格的畸变。故笔者采用结构网格的划分方式。由于砂轮与工件间隙较小,为保证间隙处的流场仿真精度,其附近的网格尺寸应取间隙宽度的1/10。

仿真几何模型及网格划分如图1所示。

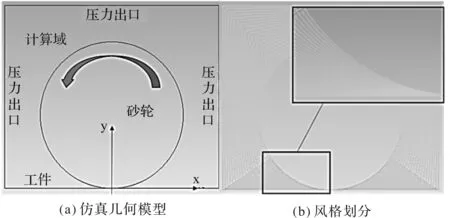
图1 仿真模型与网格

仿真参数如表1所示。

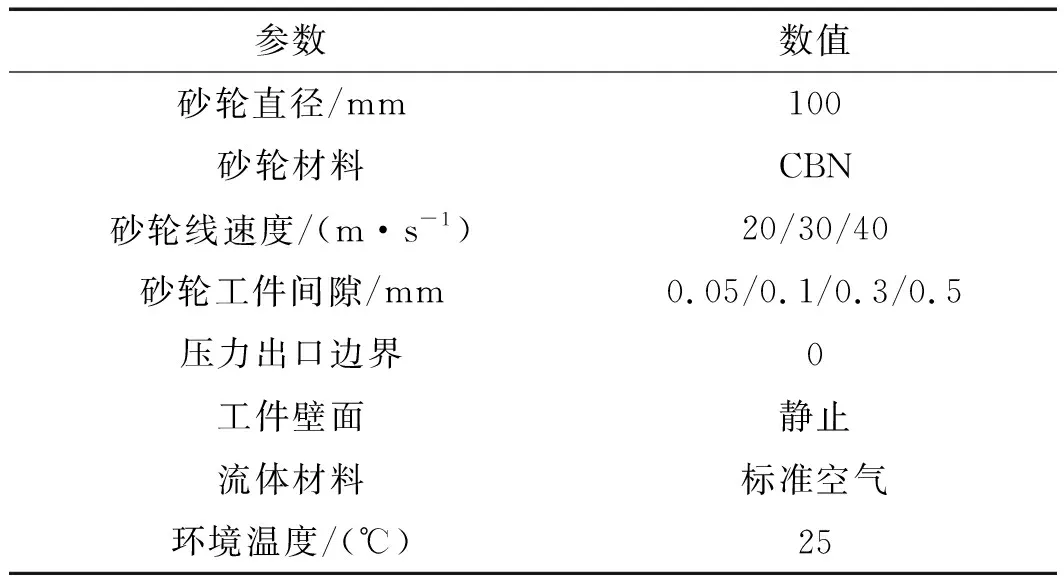
表1 仿真参数

2.2 流场压力分布分析

砂轮流场的压力分布云图如图2所示。

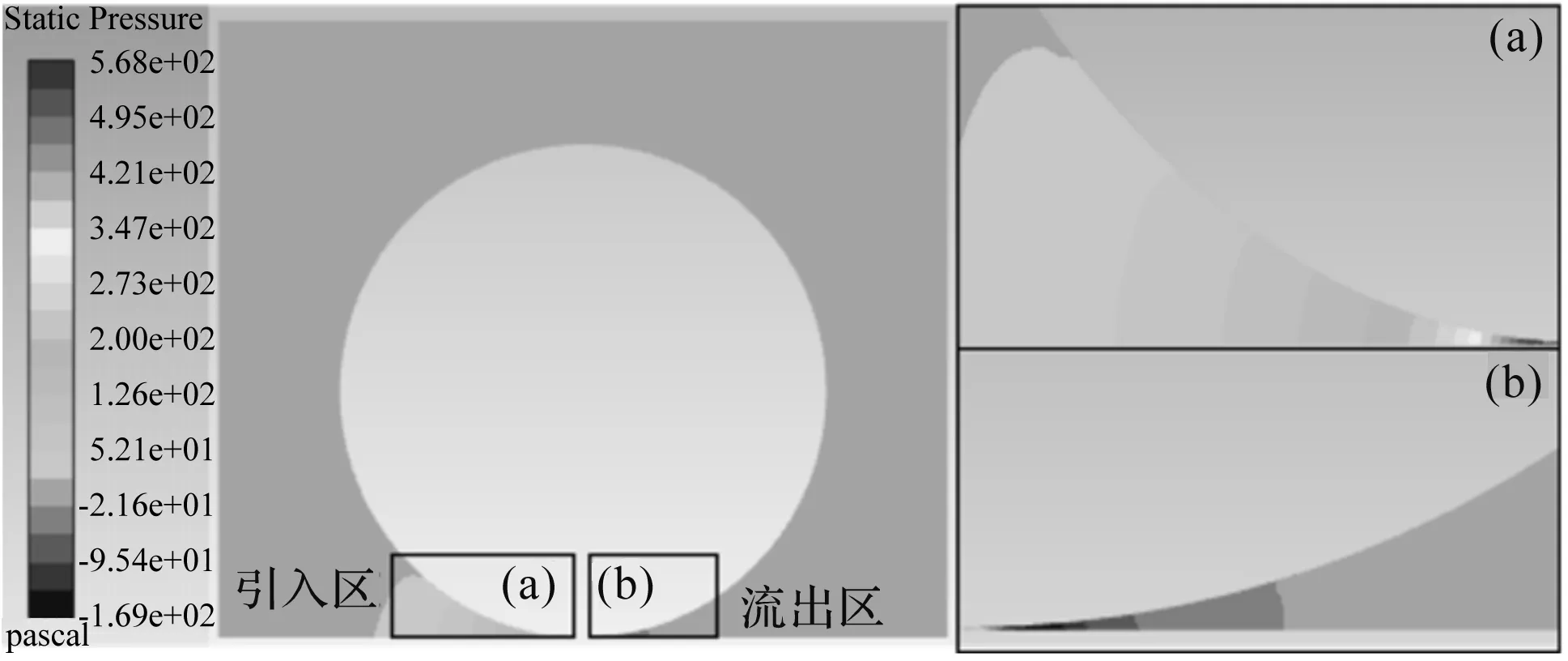
图2 砂轮流场压力分布云图

空气存在粘性,空气在砂轮的带动下流向楔形引入区,由于间隙过小,气流在此聚集,使压力高于大气压。在楔形流出区,气流随砂轮流转动流出,形成负压区。

2.2.1 最小间隙对楔形区压强分布影响

砂轮线速度为40 m/s条件下,笔者改变砂轮与工件之间的最小间隙,通过仿真得到楔形区压强分布变化情况;其中,最小间隙h分别取0.05 mm,0.1 mm,0.3 mm,0.5mm。

楔形区压强变化曲线如图3所示。

图3 不同最小间隙楔形区压力变化曲线

EBBRELL[12]214通过磨削实验对楔形区流场压力进行了测试,其压力分布曲线如图4所示。

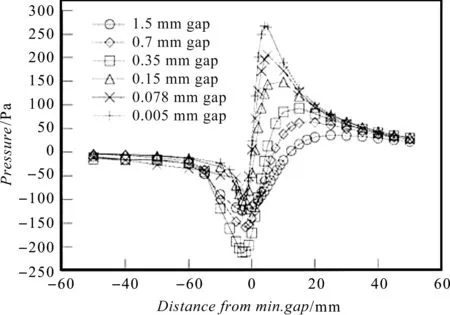
图4 EBBRELL磨削实验楔形区压力分布

对比图(3,4)可知:由于砂轮线速度方向不一致,两图中楔形区压力正负分布相反;但从压力的变化趋势来看,仿真结果与磨削实验测量结果相一致,由此可以说明,使用二维仿真模型的仿真结果是准确的。

分析图3还可知:砂轮与工件之间的最小间隙对楔形区压力分布有一定的影响;最小间隙越小,楔形区压力峰值越大,且最小间隙越小,对楔形区压力峰值影响越大;在同样的线速度条件下,在最小间隙h为0.05 mm和0.1 mm时,楔形区压力峰值远大于最小间隙h为0.3 mm和0.5 mm时的峰值。而楔形区压力越大,越不利于磨削液进入磨削区。因此,小的最小间隙不利于磨削液的有效冷却润滑。

2.2.2 砂轮线速度对磨削区压力影响

砂轮与工件之间的最小间隙h=0.05 mm,在保证上述条件不变的情况下,笔者改变砂轮的线速度,通过仿真得到磨削气流场楔形区的压力分布情况。

仿真中砂轮线速度分别为:20 m/s、30 m/s、40 m/s,得到压强变化曲线如图5所示。

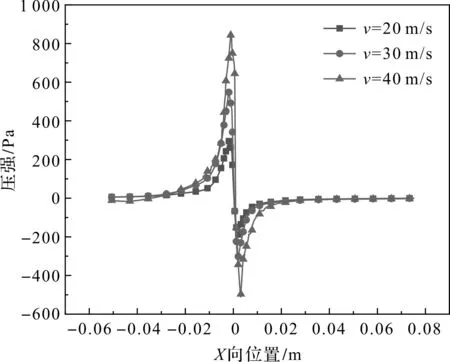
图5 不同线速度楔形区压力变化曲线

由图5可知:在最小间隙不变的条件下,砂轮线速度增大对楔形区的压强分布规律影响不大,但楔形区压强的峰值随砂轮线速度的提高而增大;楔形区压强的增大表明在楔形区的气障层增强,不利于磨削液进入磨削区,使磨削液的冷却润滑效果减弱。

2.2.3 砂轮线速度和最小间隙对压强分布综合影响分析

砂轮线速度、砂轮与工件之间的最小间隙均是影响楔形区压力分布的重要因素,但这两个因素并非相互独立,而是相互影响,共同决定楔形区域的压力分布。

笔者改变砂轮线速度和最小间隙,通过仿真获得不同砂轮线速度和最小条件下的楔形区压强变化曲线图,如图6所示。

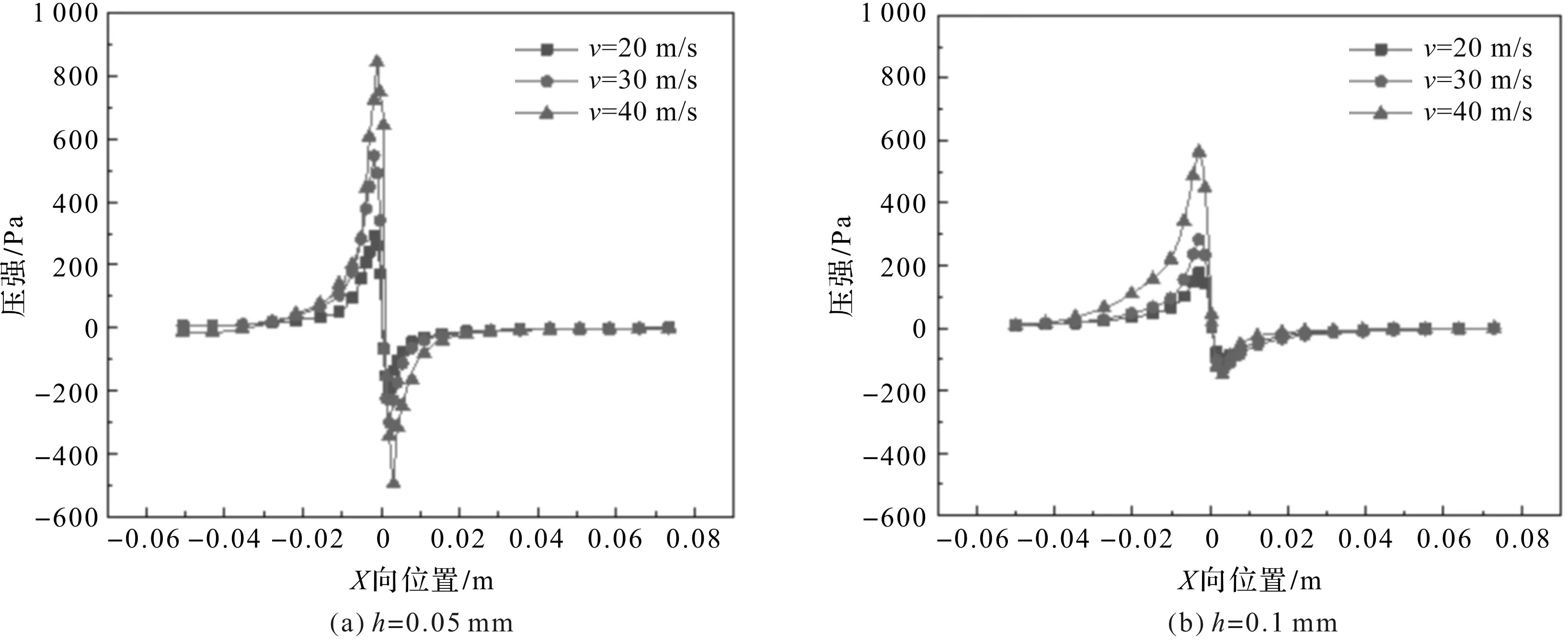
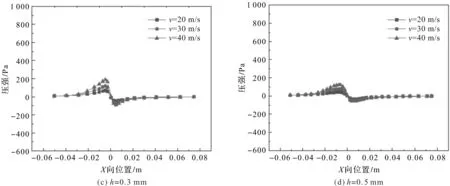
图6 磨削区压力变化曲线图

对比图6(a～d)可以发现:砂轮线速度对楔形区压强分布的影响程度取决于砂轮与工件之间最小间隙的大小;当最小间隙越小时,砂轮线速度对楔形区压强峰值影响越大。

当h=0.05 mm时,3种线速度条件下楔形区的压强峰值有着明显的差距;当h=0.5 mm时,3种线速度条件下楔形区压强差别很小,砂轮线速度对楔形区峰值影响很小。

2.3 流场速度分析

砂轮旋转时,其表面形成的气体流场会在砂轮的表面形成气障层,阻碍磨削液进入磨削区。由于空气具有一定的粘度,会随着砂轮旋转转动,在砂轮与工件之间形成楔形区间,气流运动至楔形区间后会在楔形区间聚集,形成返回流,其流向与砂轮旋转方向相反,楔形区速度矢量局部放大图如图7所示。

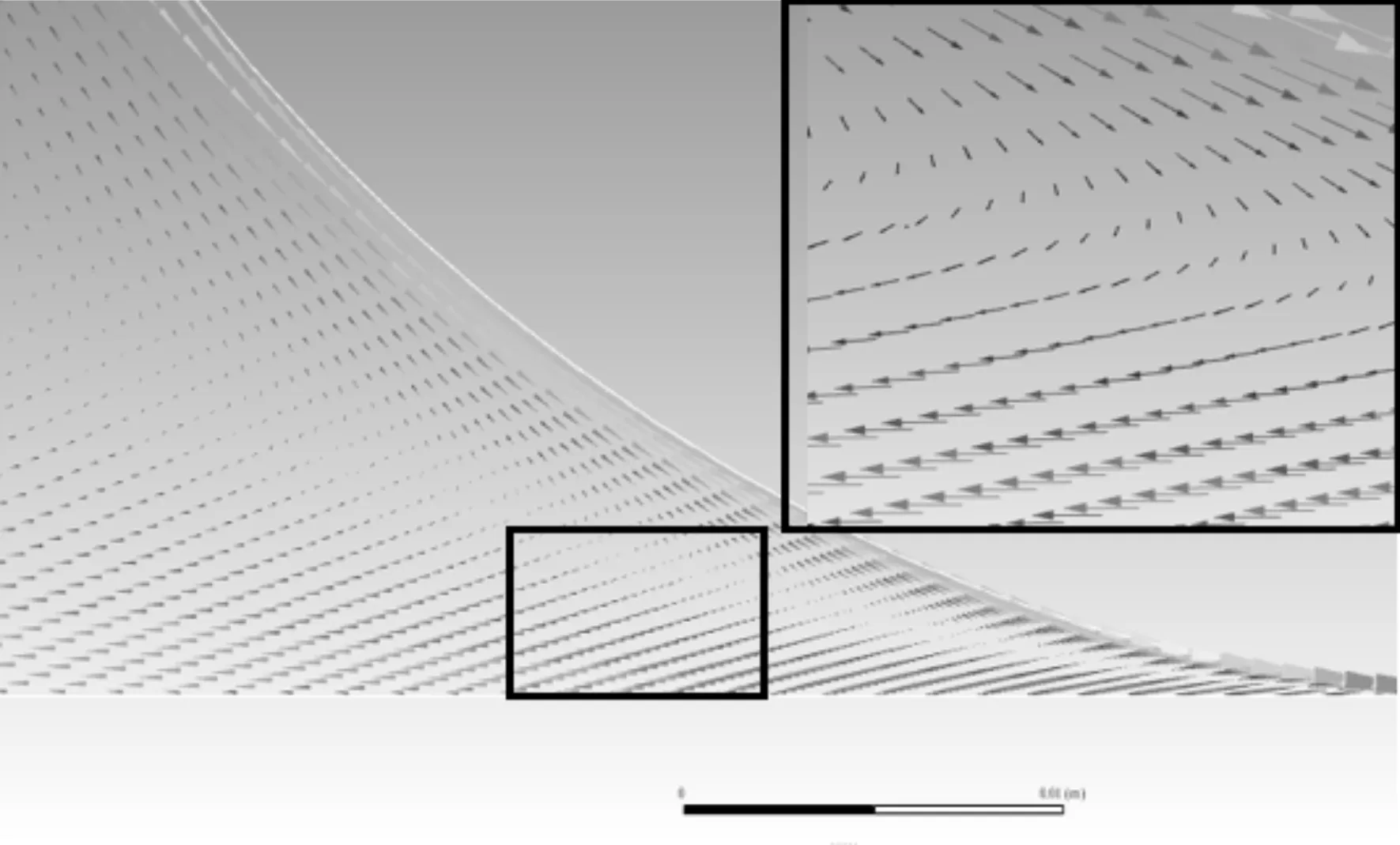
图7 楔形区速度矢量局部放大图

返回流水平方向速度由磨削区流出,对磨削液进入磨削区有很大的阻碍作用。为使磨削液进入磨削区,磨削液喷射应尽量避开返回流区域。相关研究表明,喷嘴轴线与工件表面呈一定角度(15°～20°)时[9],磨削液更容易进入磨削区。

2.3.1 砂轮线速度对楔形区速度分布影响

由上述分析可知,阻碍磨削液进入磨削区的主要是楔形区流场的水平方向分量,因此,笔者主要对楔形区水平速度分布进行研究。在最小间隙h=0.05 mm条件下进行仿真。

改变砂轮线速度,依次取20 m/s、30 m/s、40 m/s,楔形区水平速度变化曲线如图8所示。

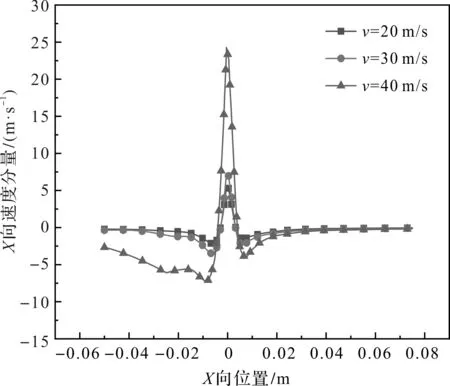
图8 水平速度分布曲线

由图8分析可知:在最小间隙附近,楔形区流场速度与砂轮线速度相一致,有利于磨削液进入磨削区;在远离最小间隙区域(-0.04 m～-0.005 m),流场速度与砂轮速度相反,形成返回流,不利于磨削液进入磨削区。

由图8还可以看出:砂轮线速度越大,返回流强度越强;并且在高速时,对返回流强度影响更明显,在较低速度时,砂轮对返回流强度影响较弱。

2.3.2 最小间隙对楔形区速度分布影响

为了研究不同条件下,砂轮与工件之间最小间隙对楔形区水平速度分布的影响,笔者取砂轮线速度值20 m/s、30 m/s、40 m/s。

砂轮与工件间的间隙取决于砂轮的形貌,其值应小于磨粒突出砂轮表面的最大高度,此处笔者分别取最小间隙值0.05 mm、0.1 mm、0.3 mm、0.5 mm进行仿真。

楔形区水平速度变化曲线如图9所示。

图9 不同间隙速度水平分量分布图

由图9可知:砂轮与工件间最小间隙对楔形区水平速度分量的分布趋势及峰值影响不大,但对楔形区返回流的强度影响较大;-0.04 m～-0.005 m区间,X向速度分量为负值,说明在该区间存在返回流;随着最小间隙减小,返回流速度越大,越不利于磨削液进入磨削区。

从图9中还可以看出:最小间隙值越小,影响程度越大;在线速度为40 m/s条件下,当最小间隙大于0.3 mm时,最小间隙对返回流无明显影响。

3 微量润滑条件下流场仿真分析

微量润滑技术是将微量的磨削液通过压缩气体进行雾化,将雾化的磨削液液滴喷入磨削区,实现冷却润滑的技术。液滴的运动轨迹将决定磨削液进入磨削区的有效流量。

笔者应用FLUENT软件[19]对砂轮流场中液滴运动轨迹进行仿真。由于存在气体和液体两种状态的流体,采用二相流模型。对于微量润滑,磨削液的量极小,液、气体积比远小于10%,故笔者将磨削液看作离散相。

在FLUENT软件中,离散相模型中共有5种雾化模型:平口喷嘴雾化模型、压力-旋流雾化喷嘴模型、转杯雾化模型、空气辅助雾化模型、气泡雾化模型。根据微量润滑工作原理,笔者选择空气辅助雾化模型进行流体仿真。

仿真模型如图10所示。

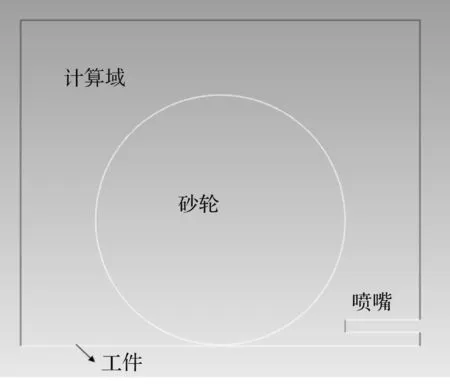
图10 流场仿真几何模型

3.1 MQL射流对砂轮流场的影响

磨削液经喷嘴雾化后,形成具有一定初速度的气、液混合射流(MQL射流)。MQL射流进入砂轮流场,会对砂轮流场形成扰动,进而影响砂轮流场的分布。根据2.2节论述,二维仿真模型适用于磨削流场的仿真。

通过仿真获得的在MQL射流影响下的楔形区域流场速度分布局部放大图,如图11所示。

图11 楔形区速度矢量局部放大图

由图11可知:MQL射流对楔形区速度分布影响较大,在喷嘴出口偏上和偏下位置均出现涡流。根据涡流的流向可以判断,涡流的存在会阻碍磨削液液滴进入磨削区,减弱磨削液的冷却润滑效果。

压强分布图如图12所示。

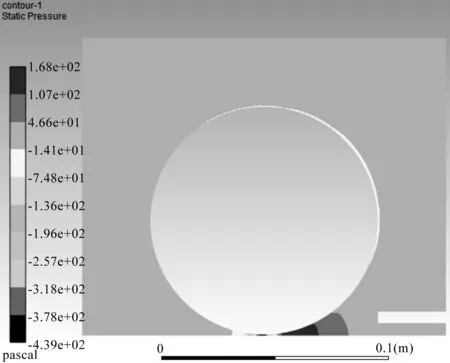
图12 流场压强分布图

根据图12可知:MQL射流会增大楔形区的压强,且扩大了高压区的范围;这样的变化对于磨削液进入磨削区是不利的。

3.2 磨削液有效流量影响因素分析

由3.1节可知,MQL射流的砂轮流场产生的影响不利于磨削液进入磨削区。但磨削液经雾化产生的小液滴具有一定的动能,当达到一定值时,可以克服砂轮流场的阻碍进入磨削区。由于磨削液密度一定,液滴动能取决于液滴的初速度和液滴体积。

根据喷雾学原理,磨削液流速和气体压强是影响液滴体积和速度的关键因素。

3.2.1 空气压强对磨削液有效流量的影响

线速度为40 m/s,磨削液流量为50 mL/h,在保证上述条件不变的条件下,笔者通过改变压缩气体压强,得到不同压强条件下磨削液液滴的运动轨迹。

压缩气体压强取值为0.2 MPa、0.4 MPa、0.6 MPa、0.8 MPa时,其液滴运动轨迹如图13所示。

图13 液滴轨迹图

图13中为MQL射流中的各液滴在砂轮流场中的运动轨迹。

对比图13可知:随着压缩气体压强的增加,磨削液液滴越容易克服砂轮流场的阻碍作用,进入磨削区,即压缩气体压强越大,磨削液进入磨削区的有效流量越大。这是由于随着压缩气体压强增大,液滴的初速度越大,越容易克服气障层和返回流的阻碍。

根据液滴碰壁理论[20],当液滴与壁面碰撞时会出现3种状态,即反弹、铺展依附在壁面、液滴飞溅破碎。但当液滴速度过大,在与壁面碰撞时,液滴破碎成小液滴飞溅入砂轮流场中,可能导致破碎的小液滴不能进入磨削区,减小磨削液的有效流量。

3.2.2 磨削液流量对有效流量的影响

在线速度为40 m/s,压缩气体压强为0.6 MPa时,在保证上述条件不变的情况下,笔者分别取磨削液流量为30 mL/h、40 mL/h、50 mL/h;通过仿真可以获得3种流量下的液滴运动轨迹图。其中,流量为30 mL/h、40 mL/h条件下的轨迹如图14所示。

流量为50 mL/h时,其液滴运动轨迹如图13(c)所示,对比图13(c)、图14可以发现:

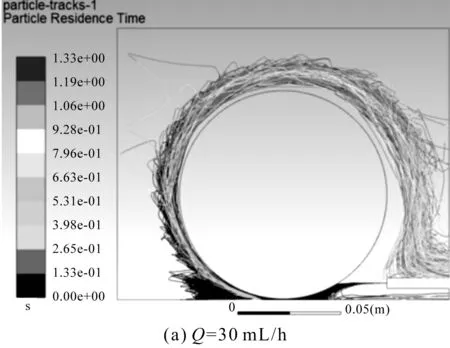
在3种流量的条件下,磨削液进入磨削区的有效流量相差不大;影响磨削液液滴穿过气障层的因素主要为气障层强度、液滴速度、液滴体积;在砂轮线速度一定的情况下,气障层强度基本相同,液滴速度和液滴体积成为影响液滴进入磨削区的主要因素;改变磨削液流量,进入磨削区的有效流量无明显变化,其原因可能是改变磨削液流量对液滴速度和体积的影响较小,进而对进入磨削区的有效流量无明显影响。

4 结束语

依据流体力学理论,本文建立了砂轮流场仿真模型,并对磨削区磨削液有效流量进行了仿真研究。

研究结果表明:

(1)在最小间隙一定的条件下,砂轮线速度越高,流场对磨削液进入磨削区的阻碍作用越强;当砂轮线速度低于某一值(临界值)时,楔形区返回流较弱,对磨削液进入磨削区影响很小;当最小间隙为0.05 mm时,砂轮线速度临界值为20 m/s;

(2)最小间隙越小,气障层对磨削液进入磨削区阻碍作用越强;最小间隙影响线速度临界值的大小,最小间隙越大,线速度临界值越大;当最小间隙分别为0.05 mm、0.3 mm、0.5 mm时,相应的线速度临界值分别为20 m/s、30 m/s、40 m/s;

(3)可以通过调节MQL参数来克服砂轮流场对磨削液进入磨削区的阻碍作用;增加压缩气体的压强可以增大磨削液液滴的速度,提高磨削液穿过砂轮流场的能力,进而提高磨削液进入磨削区的有效流量。但压缩气体压强过高,会导致液滴碰壁飞溅进入砂轮流场,减小有效流量。线速度在40 m/s时,气体压强应不超过0.6 MPa。由于微量润滑使用的磨削液量很小,改变磨削液流量对有效流量影响很小,仅仅从砂轮流场角度考虑,可以忽略磨削液流量变化对有效流量的影响。

在后续研究中,笔者会进行微量润滑磨削的磨削区流场实验,通过实验研究砂轮线速度、最小间隙对磨削区流场分布的影响,并通过实验获得磨削液在流场中的状态,分析砂轮线速度、气体压强、磨削液流量对进入磨削区有效流量的影响规律。