塔式摩擦提升机的动力学建模及其纵向振动分析*
2021-08-06黄家海王文庆
郭 瑜,黄家海,赵 斌,王文庆,刘 畅
(太原理工大学 机械与运载工程学院,山西 太原 030024)
0 引 言
作为矿井关键运输设备,摩擦提升机随矿井深度不断增加逐渐向高速、重载方向发展。摩擦式提升机分为塔式和落地式两种。塔式摩擦提升机有如下优点:(1)钢丝绳的包围角大,有利于防滑;(2)钢丝绳在井塔内,不受雨雪影响,对防滑性能影响小;(3)钢丝绳弯曲点少,使用寿命更长[1]。
近年来,国内外学者对摩擦提升系统的振动特性展开了大量研究。KACZMARCZYK S等[2]建立了矿井提升系统的分布参数数学模型,通过Rayleigh-Ritz法离散偏微分方程,以分析钢丝绳的横向-纵向耦合动力响应,并研究了提升系统运行过程中的瞬态共振现象。MA C等[3]基于功率平衡法将钢丝绳简化为杆件,建立了其动力学模型,通过里兹级数法离散振动偏微分方程;研究结果表明,钢丝绳长度和箕斗质量对冲击时间和每一阶的振动频率均有影响。YAO J N等[4-5]基于Hamilton原理建立了落地式摩擦提升机的多源耦合动力学模型,分析了不同提升参数对系统横向振动的影响。WANG N G等[6]建立了柔性提升系统的横向-纵向耦合动力学模型,通过数值计算和ADAMS仿真分析系统的动态响应;研究结果表明,当外界干扰频率接近系统固有频率时,系统会发生明显的共振。SANDILO S H等[7]将提升系统简化为一端附有集中质量的运动弦线模型,通过多重尺度法构造近似解析解,分析了绳长线性变长或谐波变长时系统的非线性动力学响应。文献[8-10]利用商业动力学仿真软件RecurDyn,建立了落地式摩擦提升机的仿真模型,并对运行过程中的振动特性进行了分析研究。
上述学者在研究中通常忽略尾绳的作用或者将其质量等效至提升容器[11],而实际运行过程中不仅提升绳的长度随时间变化,尾绳的长度同样是时变的。随矿井深度增加,尾绳的长度和质量增加,对提升系统纵向振动的影响是不可忽略的。
本研究以塔式摩擦提升机为研究对象,建立提升机动力学模型,对提升系统的纵向振动进行仿真分析和试验、研究。
1 提升系统纵向振动模型
塔式摩擦提升机简化动力学模型如图1所示。
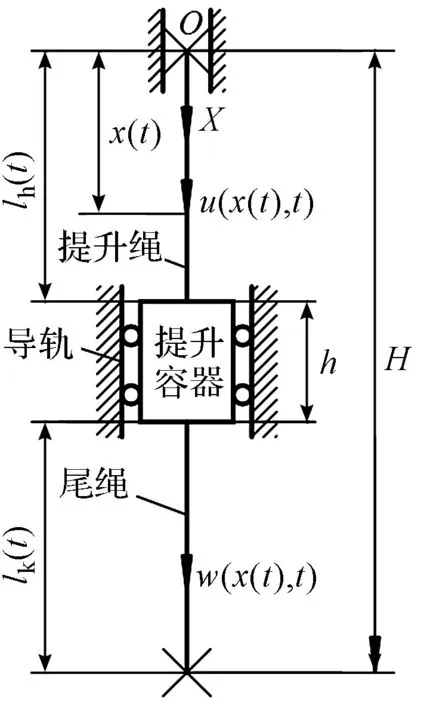
图1 摩擦提升系统示意图lh(t)—提升绳长度;lk(t)—尾绳长度;u(x,t)—提升绳纵向振动;w(x,t)—提升绳纵向振动;h—提升容器高度;H—井深
图1中,笔者以提升绳上端即钢丝绳与摩擦轮相切处为原点建立坐标系,忽略钢丝绳打滑,将尾绳下端视为自由端[12]。提升绳和尾绳均为弹性体,长度均为变量,假设其具有均匀性和连续性且遵循胡克定律,在运行过程中分别发生纵向振动;提升容器与罐道为刚性体。
1.1 纵向振动控制方程
系统x处的位移向量R为:
(1)
式中:i—沿X轴的单位矢量。
对时间变量t求导,可得提升绳和尾绳的速度向量V1和V2为:
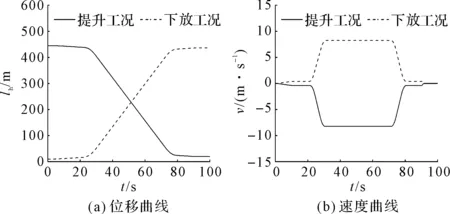
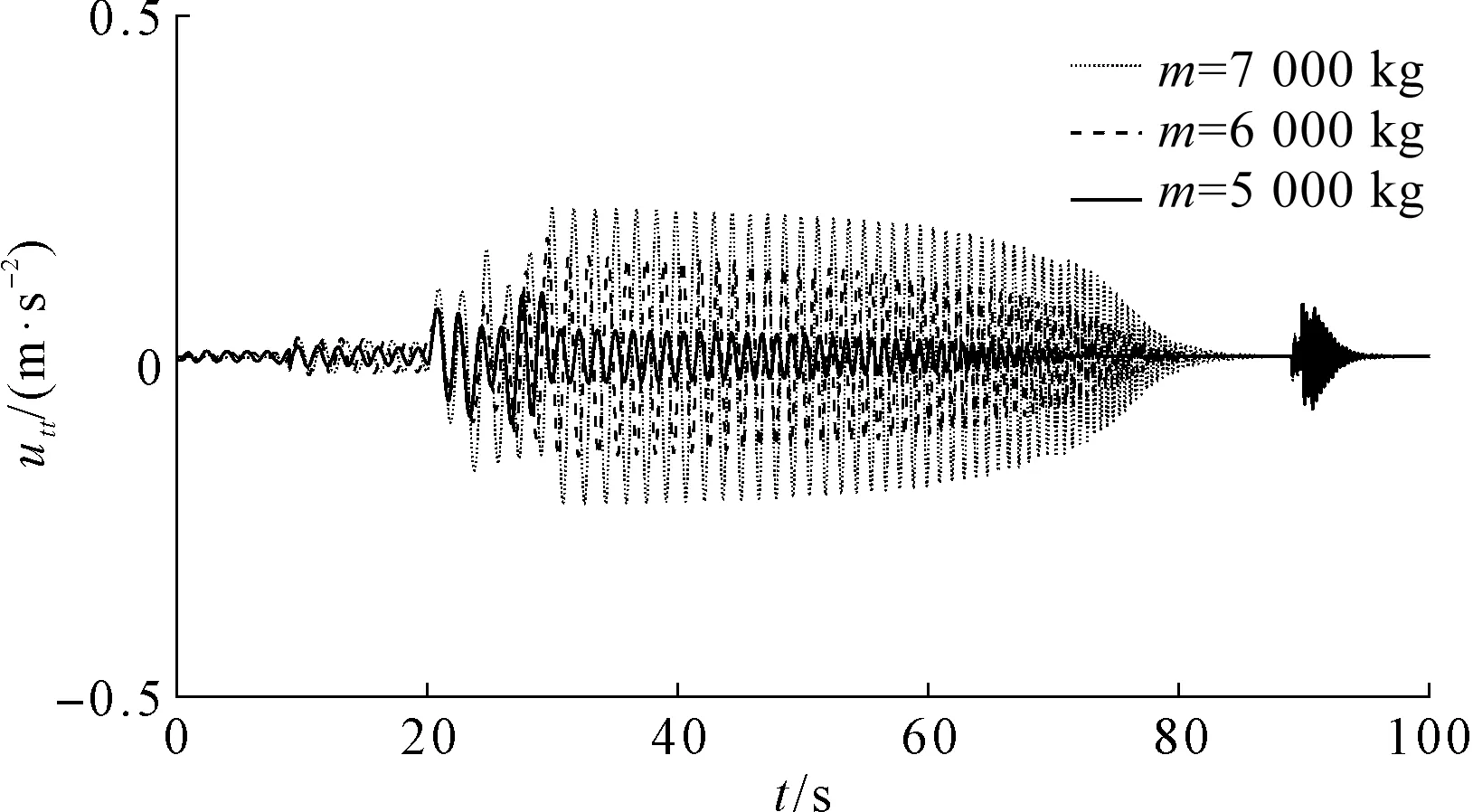
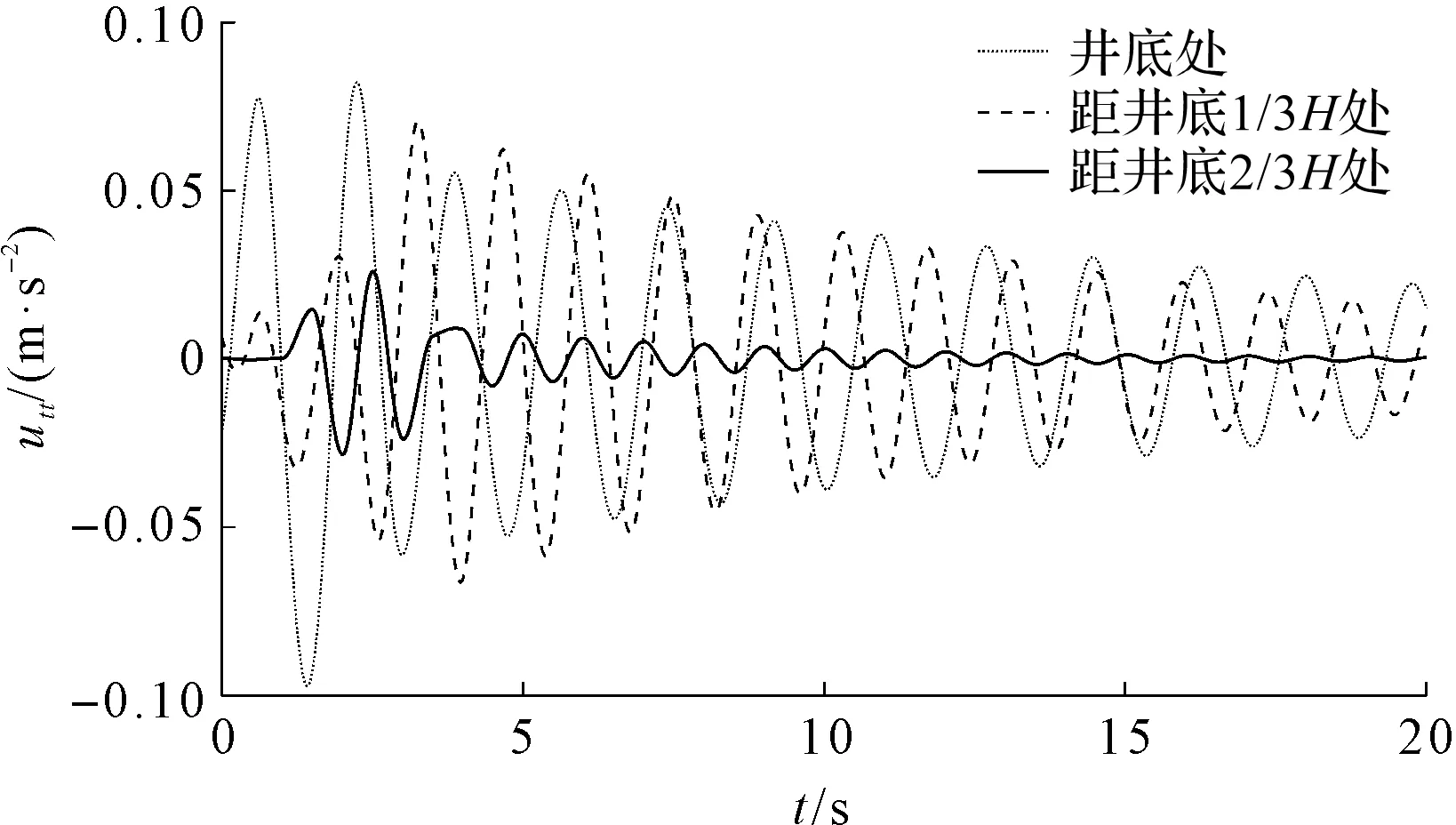
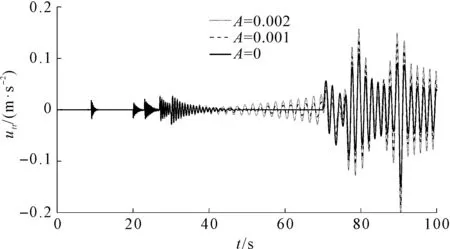
V1=[v(t)+ui(x,t)+v(t)ux(x,t)]i, (2) V2=[v(t)+wt(x,t)+v(t)wx(x,t)]i, (3) 式中:v(t)—提升系统的运行速度,m/s。 为方便书写,上标“·”表示对时间的全导数,下标t,x分别表示对时间和空间的偏导数,下面的方程中将v(t),u(x,t)和w(x,t)简写为v,u和w。 摩擦提升系统动能为: (4) 式中:ρ1,ρ2—提升绳和尾绳的线密度,kg·m-1;m—提升容器的质量,kg。 摩擦提升系统弹性势能为: (5) 式中:E1,E2—提升绳和尾绳的弹性模量,GPa;A1,A2—提升绳和尾绳的横截面积,mm;Th(x,t),Tk(x,t)—提升绳和尾绳的准静态张力[13],N。 其中: Th(x,t)=[m+ρ1(lh(t)-x)+ρ2(H-lh(t)-h)]g (6) Tk(x,t)=ρ2(H-x)g (7) 式中:g—重力加速度,m/s2。 摩擦提升系统重力势能为: (8) 提升系统振动过程中阻尼耗散能为[14,15]: (9) 式中:μ1,μ2—提升绳和尾绳的纵向阻尼系数。 将式(4,5,8,9)代入广义Hamilton原理中: (10) 应用莱布尼兹法则和变分运算,可得摩擦提升系统钢丝绳和尾绳的振动控制方程: (11) (12) 由于提升绳下端与提升容器顶部相接,尾绳上端与提升容器底部相接,考虑二者边界的相互作用,振动偏微分方程相应的边界条件为: u(0,t)=0,u(lh(t),t)=w(lh(t)+h,t) (13) (14) v+wt(H,t)+vwx(H,t)=0 (15) 由于纵向振动控制方程为带有时变参数的偏微分方程组,难以获得解析解,笔者通过Galerkin法将偏微分方程离散为常微分方程组,使用MATLAB软件进行数值求解。 此处引入无量纲变量ξ、ζ对式(11,12)进行归一化处理,其中: (16) 将方程从时变空间域转化为ξ和ζ的固定域[0,1],则方程的解可以表示广义坐标和满足方程边界条件振型函数的线性组合[16]: (17) 式中:pk(t),qk(t)—第k阶广义坐标;n—模数;φk(ξ),ψk(ζ)—离散提升绳和尾绳振动方程的振型函数。 其中: (18) 求出振动位移u(x,t)和w(x,t),对t和x的各阶偏导,代入振动控制式(11,12),并分别乘以φk(ξ)/lh(t)和ψk(ζ)/lk(t),其中: (19) (20) (21) (22) 笔者利用Galerkin加权余量法将ξ和ζ在固定域[0,1]内进行积分,将振动控制偏微分方程组离散为常微分方程组: (23) 式中:p,q—广义坐标向量,p=[p1,p2,…,pk]T,q=[q1,q2…,qk]T;M1,M2—与p和q对应的质量矩阵;C1,C2—与p和q对应的刚度矩阵;K1,K2—与p和q对应的阻尼矩阵;F1,F2—与p和q对应的广义力矩阵。 M1、C1、K1和F1的元素值为: (24) (25) (26) (27) 其中: φ(ξ)=[φ1(ξ),φ2(ξ),…,φk(ξ)]T (28) (29) (30) (31) (32) (33) M2、C2、K2和F2的元素值为: (34) (35) (36) (37) 其中: ψ(ζ)=[ψ1(ζ),ψ2(ζ),…,ψk(ζ)]T (38) (39) (40) (41) (42) (43) (44) 摩擦提升系统运行过程中,系统不可避免地会发生纵向振动。 笔者以某矿JKM-3.5X6Z(Ⅲ)型塔式摩擦提升机参数作为输入量,对理论模型进行了仿真分析。提升绳的基本参数为线密度ρ1=5.024 kg·m-1,弹性模量E1=9.2 GPa,横截面积A1=36 mm,纵向阻尼系数μ1=3×10-3,尾绳的基本参数为线密度ρ2=6.048 kg·m-1,弹性模量E2=8.9 GPa,横截面积A2=34 mm,纵向阻尼系数μ2=3×10-3。提升容器质量m=5 400 kg,提升绳的初始长度为15 m,井深H=530 m。系统运行过程中,输入速度曲线由提升机摩擦轮转速拟合得到,通过数值积分和微分得到系统运行过程中的位移和加速度曲线。 提升系统运动曲线如图2所示。 图2 提升系统运动曲线 以上述提升参数和运动曲线作为输入量,笔者应用MATLAB软件和Runge-Kutta法,对四阶Galerkin截断得到的常微分方程组进行数值计算。 提升工况下,提升容器上方2 m处提升绳与距提升容器底部2 m处尾绳的纵向振动响应,如图3所示。 图3 提升工况下系统振动响应 图3中:提升工况下提升绳与尾绳的纵向振动位移趋势相同,这是因为提升绳的下端和尾绳的上端分别与提升容器顶部和底部相接,两者边界的耦合使振动互相影响,但提升绳的纵向振动比尾绳更剧烈; 随提升容器提升,提升绳长度减小,提升绳与尾绳的振动频率均会明显增加;系统加速时,提升绳和尾绳的振动位移达到峰值;系统加速、减速和制动时,提升绳和尾绳纵向振动加速度幅值明显增加,随后在钢丝绳内部阻尼作用下振动逐渐衰减;与提升绳不同,减速时尾绳的振动加速度达到峰值,这是因为提升工况下减速时尾绳长度比加速时更长,系统运动状态突变产生的惯性冲击会使尾绳产生更剧烈的振动。 下放工况下,提升容器上方2 m处提升绳与距提升容器底部2 m处尾绳的纵向振动响应,如图4所示。 图4 下放工况下系统振动响应 图4中,下放工况下提升绳与尾绳的纵向振动比提升工况更小。随提升容器下放,提升绳长度增加,提升绳与尾绳的振动频率均会明显增加。系统减速时,提升绳和尾绳的振动位移达到峰值。系统下放过程中减速和制动会导致提升绳和尾绳产生较大的纵向振动加速度。加速时尾绳的振动加速度达到峰值。 系统制动后提升绳纵向振动对比如图5所示。 图5 系统制动后提升绳纵向振动对比 由图5可知:提升容器下放至井底处时,提升绳与尾绳振动加速度更大,且阻尼衰减率明显小于提升工况,系统恢复稳态需要更长的时间。这是因为下放制动时提升绳长度比提升制动时更长,钢丝绳刚度较小,受冲击作用产生的振动更加剧烈,且提升制动时提升容器的惯性力方向于重力加速度方向相反,系统制动过程中耗散的能量更多。 为验证理论模型,笔者对某矿JKM-3.5X6Z(Ⅲ)型塔式摩擦提升机进行振动特性测试。 测试系统布局如图6所示。 图6 测试仪器布局示意图 图6中,将KISTLER 8795A50型可变电容式三轴加速度传感器置于罐笼内部,采集系统运行过程中的纵向振动信号。由于被测矿井深度达到500 m,无法通过线路连接直流电源为测试仪器供电。因此,将铅蓄电池的直流电转换为220 V交流电。 加速度传感器参数如下:测量范围为±50 g,分辨率为0.001 g,灵敏度为100 mV/g,谐振频率20 kHz。由采样频率为100 Hz的NI USB-6343型数据采集卡将采集到的纵向振动信号传送至电脑中,使用LabView软件存储数据;最后,使用MATLAB软件设计低通滤波器对数据进行滤波。 测试现场图如图7所示。 图7 测试现场 仿真与测试曲线对比如图8所示。 图8 仿真与测试曲线对比 图8中,本文建立的动力学模型计算得到的振动加速度幅值与实验测试结果在相同位置的振动加速度幅值基本一致。从仿真和实测曲线均可看出:系统加速、减速时振动加速度明显增大,制动时系统受到冲击产生纵向振动峰值,随后在内部阻尼的作用下衰减为0。由此表明,本文建立的带尾绳提升系统动力学模型和使用不同振型函数通过Galerkin加权余量方法计算系统的纵向振动是可行的。 由于理论模型采用了一些假设,致使仿真曲线与试验测试曲线存在一定的误差,例如忽略了系统运行过程中摩擦轮和刚性罐道对钢丝绳上下边界的扰动,导致仿真结果中匀速阶段钢丝绳的振动均小于真实值。综上可知,本文建立的带尾绳提升系统振动模型能够反映系统的纵向振动特性。 随着矿井深度变深,提升速度越来越快,摩擦提升系统在运行过程中对结构参数变化更加敏感。此外,由摩擦轮输出转速或力矩的波动、动不平衡会在钢丝绳与摩擦轮分离处产生纵向激励源,该激励可能引起提升系统运动状态参数发生波动,进而引发参数激励振动现象[17]。 提升质量分别为5 000 kg、6 000 kg和7 000 kg时系统的纵向振动响应[18],如图9所示。 图9 不同提升质量时提升绳振动响应 图9中,提升质量越大,提升系统运行过程中纵向加速度幅值越大。制动后,提升质量越小,系统的残余振动更剧烈;摩擦提升机重载运行时,系统更易产生剧烈的纵向振动,但由于钢丝绳张力增大,制动后产生的残余振动更小。 提升容器下放至井底处、距井底1/3H处和距井底2/3H处制动时,系统的纵向振动响应如图10所示。 图10 不同高度制动时系统振动对比 图10中,当提升容器越靠近井底时,提升绳长度变长,瞬时刚度较小,系统运动状态突变更易导致剧烈的纵向振动。因此,当井深变深、钢丝绳总长变长,即系统提升高度增加时,加速、减速和制动时会产生更严重的纵向振动。 假设提升绳上端存在一个纵向谐波激励,e(t)=A0sin(πt),受该激励影响,提升绳瞬时长度为lh(t)+e(t)。激励幅值分别为0 m、0.001 m和0.002 m时系统的纵向振动响应如图11所示。 图11 不同激励幅值时系统振动对比 图11中,随激励幅值增大,系统纵向振动加速度幅值明显增加。该谐波激励不仅使钢丝绳绳长发生变化,也会导致系统的运行速度和加速度发生突变。因此,摩擦轮作为摩擦提升系统的动力源,除提供动力外,其引入的边界激励也会导致提升机产生受迫振动。 针对塔式摩擦提升机纵向振动特性,笔者应用Hamilton原理建立了带尾绳摩擦提升系统纵向振动偏微分方程;以矿井塔式提升机参数和运动状态曲线作为输入,对系统运行过程中的纵向振动相应进行了仿真分析和验证,研究了提升参数对系统振动特性的影响。研究结果表明: (1)提升系统加、减速和制动时,提升绳和尾绳纵向振动位移和加速度均会明显增加,在内部阻尼作用下振动逐渐衰减(提升绳与尾绳的纵向振动特征与此相似);系统下放到井底制动时纵向振动位移和加速度均大于提升工况,且阻尼衰减率更慢; (2)提升载荷、高度以及摩擦轮波动幅值的增加均会使系统运行过程产生更剧烈的纵向振动; (3)经实验验证,笔者建立的带尾绳纵向振动模型能够较好地描述塔式摩擦提升系统的纵向振动特性。
0
lh(t)+h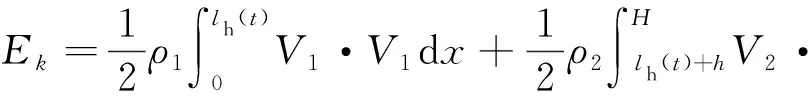


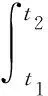



1.2 振动方程离散化
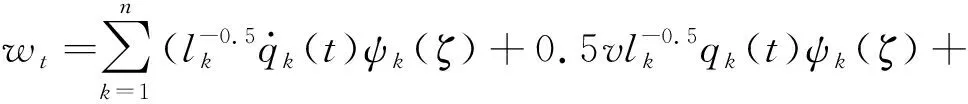


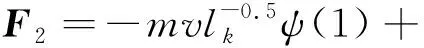
2 纵向振动仿真与试验
2.1 纵向振动响应仿真及分析



2.2 纵向振动响应试验及分析



3 提升参数对系统振动特性影响
4 结束语
