一种基于模拟惯量偏差的电惯量控制算法

帅忠全，高 飞，祁 伟，符 蓉

（大连交通大学 连续挤压教育部工程研究中心，大连 116028）

列车制动试验台是模拟列车的制动工况并研究摩擦材料性能的重要手段。当制动试验台完全采用机械飞轮的方法模拟制动过程，就需要采用多个不同质量的飞轮组合来模拟不同列车的质量，但是由于飞轮的数量是有限的，因此存在无法模拟任意车辆载荷的困难，并且随着列车载重的增加，要求飞轮的质量越来越大，大质量飞轮的加工过程及加工精度都显著增加了试验台的制造成本。因此，在机械惯量的基础上，增加电惯量模拟功能来替代机械惯量盘就成为了车辆制动试验台的发展趋势[1]。

电惯量模拟就是在制动过程中通过控制电机的输出，产生与机械惯量等效的制动效果[2-4]。目前的电惯量模拟控制方法主要可分为转速控制法、能量补偿法、转矩控制法。转速控制法是通过控制电机转速与相应的机械惯量条件下的转速一致来模拟目标惯量。这种方法模型简单，转速变化受转矩的波动影响较小，但由于动态响应差，存在很大的滞后性而鲜有使用。能量补偿法是在制动过程中，根据能量耗散模型，控制电机输出的动能与相应的机械惯量的制动能量一致，从而模拟出机械惯量的制动效果。能量补偿法控制手段灵活，但由于难以建立精确的制动能量模型，并且能量补偿的精度依赖于电机的控制精度，故适用性较差。转矩控制法主要是基于电惯量模拟的角减速度与相应的机械惯量的角减速度等效原理，根据实时的摩擦制动转矩的大小来调节电机输出的转矩，以反馈调节制动角减速度，使之与纯机械惯量下的角减速度一致，从而模拟机械惯量的制动效果。转矩控制法由于模型简单、响应速度快、不存在累积误差等特点，是现阶段被广泛应用的控制方法。但转矩控制法由于受摩擦副的摩擦性能影响，存在精度低、惯量波动较大的问题。

以上三类控制算法均是依据理想机械惯量下的动力状态来控制电机的输出，即在惯量模拟的计算中，以模拟的机械惯量为目标惯量，建立电机输出与转速、制动转矩、制动能量的关系，从而实现模拟过程[3]。然而，由于这些参量均与制动摩擦副的摩擦性能密切相关，而摩擦副的摩擦性能是实时变化的，造成电机输出扭矩总是处于波动状态，这样，制动转矩及电机转矩两者处于一种相互关联的波动状态，使转动系统的运动、受力、能量状态十分不稳定，模拟的惯量就很难控制为常数[2-3]，这就使如何保证惯量模拟的精度成为了难题。

尤其是随着车辆的负荷增加，制动试验台需要模拟的惯量增大，模拟误差将会导致制动试验数据与实际工况有更大差距。因此，如何提高电惯量的模拟精度是电惯量模拟技术的关键问题。

针对惯量模拟的精度及瞬时惯量波动问题，本文利用转矩控制法进行制动试验，通过瞬时惯量曲线、平均模拟惯量及精度、标准差等计算值，分析了惯量模拟精度及波动程度的影响因素。为了避免受系统阻力、角加速度计算时滞等因素的影响，提出了惯量偏差控制算法，即直接依据瞬时模拟惯量及平均转动惯量相对于目标值的偏差大小而进行控制，同时针对不同的瞬时惯量偏差及平均惯量偏差，分别建立了不同的控制策略，从而达到减小惯量波动、提高模拟精度的目的。

惯量偏差控制算法与转动系统固有的阻力无关，并且所用判据不受机械系统阻力、角加速度计算时滞的影响，从而有效提高惯量模拟的精度。通过对比试验证明：利用惯量偏差控制算法使瞬时惯量波动减小了60%，惯量模拟精度提高了2%～10%。这种控制算法为惯性制动电惯量模拟技术提供了参考。

1 电惯量模拟转矩控制模型分析

转矩控制法是根据制动转矩或制动角减速度来控制电机输出的转矩，从而实现惯量模拟的一种控制方法。其计算是建立在如下的方法上的：

假设基础惯量（转动轴、电机及制动盘）为I0，忽略系统阻力矩，当安装Ie大小的机械惯量盘时，转动系统具有的机械惯量总和I为：

制动过程中，断开电机与转动系统的连接，任意i时刻的制动转矩为Tb(i)，制动角减速度为dωdt，转动系统动力学方程为：

当不安装Ie大小的机械惯量盘，在制动过程中，采用电机向转动系统输出大小为Tb(i)的转矩，使角减速度与纯机械惯量相同。模拟机械惯量I，则存在以下关系：

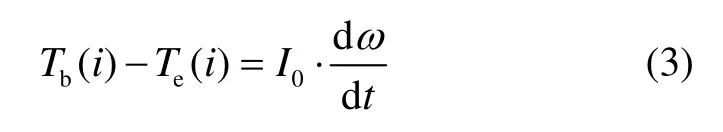
此时，若能够控制电机转矩Te(i)按照：

输出，使式(3)中的角减速度与式(2)在任意时刻均相同，即认为是对电惯量Ie的模拟[4]。由式(4)可知，可通过角减速度与制动转矩两种方式来模拟电惯量。制动扭矩与制动角减速度是电机需要输出的转矩的单变量函数，而制动扭矩和角减速度均可由传感器测得，这样就可通过试验台的测控系统将每个制动时刻的制动扭矩和角减速度的采集值经过式(4)计算后，得出电机需要输出的转矩值Te(i)，从而控制转动系统输出机械惯量相同的角减速度，模拟电惯量Ie。

由式(4)可知，转矩控制法是一种较强依赖实时数据采集的惯量模拟方法，仅依据实时的角减速度或者制动转矩控制电机的转矩输出，由于实时角减速度与制动转矩均可测，理论上，转矩控制法可以精确地模拟电惯量。但由于电机转矩的输出的作用效果，即转动系统的角减速度是由制动转矩Tb(i)及电机转矩Te(i)共同作用，Tb(i)受到制动材料性能、机械振动的影响，必然产生波动，依据这些存在波动的数据模拟出的模拟惯量与目标惯量有多大偏差，只有通过试验来进行验证。

2 转矩控制法模拟效果分析

采用基于加速度等效的转矩控制方法进行制动试验，通过变频器控制一台三相交流异步电动机，模拟55 kg·m²的目标惯量。试验台固有机械惯量为 38 kg·m²，电机转矩响应时间为5 ms，可保证转矩控制的实时性。通过数据采集卡，采集转速传感器、制动转矩传感器的信号，数据采集频率100 Hz。通过数据采集卡的模拟量输出功能，控制电机输出的转矩。试验设定制动初始速度为60 km/h，闸片单侧压力为2.6 kN。

惯量模拟的波动及精度可通过瞬时模拟惯量Isima及惯量模拟精度σsim来衡量。根据UIC-548标准，使用式(5) 来计算瞬时模拟惯量、平均模拟惯量，以及电惯量模拟精度。

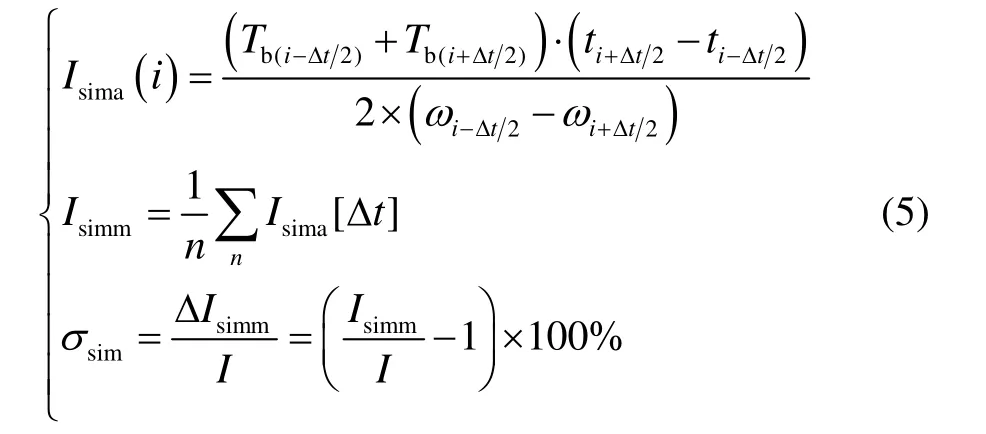
式中，Isima为瞬时模拟惯量，I为目标模拟惯量，Isimm为平均模拟惯量，T为制动转矩，i为数据采集时间点，σsim为惯量模拟精度，Δt为采样间隔。

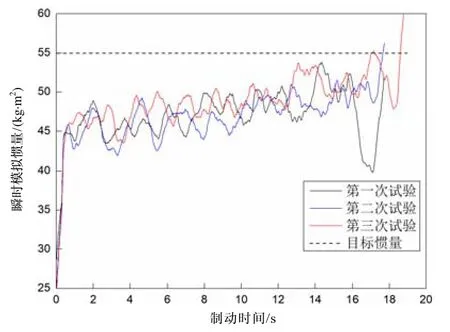
图1 转矩控制法瞬时模拟惯量曲线Fig.1 Instantaneous simulation inertia by torque control method

试验得到的瞬时模拟惯量随时间变化曲线如图 1所示。为了曲线显示清晰，在保留曲线波动的基础上，对瞬时模拟惯量数据做S-G滤波，滤波窗口宽度为12。可以看出，在制动时间1 s至19 s期间，3次试验的瞬时惯量在2 s内波动幅度至少在5 kg·m2以上，并且在制动末端，即16 s至19 s内，产生了较大程度的波动。0至18 s内的瞬时惯量均低于目标惯量55 kg·m2，在制动时间2 s内，模拟惯量与目标惯量偏差为10 kg·m2左右，仅为目标值的82%。随着制动时间的增加，模拟惯量与目标值的差距减少。

表1 转矩控制法平均模拟惯量及惯量模拟精度Tab.1 Average simulation inertia and simulation precision in torque control method

表1是由瞬时模拟惯量计算得到的平均模拟惯量及模拟精度，可以看出，3次试验的平均模拟惯量比模拟目标惯量小 9 kg·m2，而惯量模拟误差也均高于10%。标准差反映了瞬时模拟惯量值相对于平均模拟惯量的偏离程度，从表1可看出，三次试验波动情况均没有较大差别。表1计算了每个数据采集点的瞬时模拟惯量偏差高于 5 kg·m2的情况占整体瞬时惯量数据的比例，结果显示三次制动试验中这一比例均超过了70%。

从图1及表1综合分析可知：

1）在制动过程中，三次试验的瞬时模拟惯量均低于模拟目标惯量 55 kg·m²。这是因为系统固有阻力矩的存在使转动角减速度偏大，根据式(5)可知，角减速度偏大使瞬时惯量偏小[2]。

2）从整体曲线波动情况及瞬时模拟惯量偏差占比来看，瞬时惯量波动均较大，最大偏差达到 25 kg·m²，并且瞬时惯量偏差较大的时间持续较长。对于试验1，t=16 s至t=18 s内惯量波动剧烈，在t=17 s时甚至低于40 kg·m²；对于试验3，在t=19 s附近也有较大波动。这主要有两方面原因：一是由于在制动过程中，闸片性能是不断变化的，这就会使摩擦制动转矩产生波动。而转矩控制法直接由制动转矩Tb(i)的大小来调节电机输出的转矩Te(i)，这样就造成输出信号也具有较大波动，瞬时模拟惯量波动就很大；二是角减速度相对于制动转矩存在延时[5]，由于电机转矩可认为是相对于某个制动转矩数据采集点的准确值，但在这个数据采集点处的电机转矩产生的作用效果却需要根据Δt时间后的转速来衡量，即角减速度相对于制动转矩就存在着滞后，使得转矩与角减速度无法对应，产生较大的瞬时模拟惯量偏差。例如，对于试验1的瞬时模拟惯量曲线，在t=16 s时刻，制动转矩波动至极小值后逐渐增大，转矩控制法根据转矩极小值，由式(4)求解出的电机在t=16 s应输出转矩的控制量也偏小，即这一时间段内的系统合力矩偏大，于是在之后的Δt时间内便产生了较大的角减速度，瞬时模拟惯量就偏小。由于转矩的输出受频率限制，角减速度相对于制动转矩又存在着滞后，下一个时刻瞬时模拟惯量就具有较大的偏离，从而形成较大的瞬时惯量波动。

3）Isima的计算值并未与目标模拟惯量I呈现出任何相关性，即瞬时惯量并不围绕目标模拟惯量55 kgm²而波动，并且瞬时惯量偏差较大时，时间持续较长。这主要是由于转矩控制法仅根据Tb(i)和制动角减速度对电机转矩进行调节，而实时惯量大小Isima并不仅仅与制动转矩有关，还受角减速度的影响。虽然可以根据实时制动转矩输出准确的电机转矩，但是当实际模拟惯量明显偏离目标惯量时，控制算法中没有考虑对输出量进行修正。

综上所述，对于转矩控制法，系统阻力会影响惯量模拟的精度，也难以通过优化转矩的控制策略而提高惯量模拟的精度。同时，摩擦材料性能参数的变化、机械震动以及角减速度的计算滞后，都会使瞬时模拟惯量具有较大的波动。

针对这些问题，如果能兼顾转矩控制法快速响应的优点，对系统阻力进行补偿修正[6]，或者避免系统阻力矩对控制算法的影响，不再依据单一的制动转矩信号进行控制，则可以改善惯量的波动问题，同时提高模拟精度。由此，本文提出了惯量偏差控制算法。

3 惯量偏差控制算法的提出及控制模型的建立

惯量偏差控制算法是直接利用转动惯量的测量值来计算惯量模拟的偏差，根据偏差量反馈调整电机转矩输出，达到减小惯量偏差的目的。

在制动过程中，根据能量守恒定律，任何时刻均存在恒等式：

式中，E为制动闸片消耗的能量即摩擦功，Im为转动惯量，eω为任意时刻转动角速度，0ω为制动初始角速度，Ef为机械系统固有阻力损耗。

实际摩擦功是每个数据采集间隔内的瞬时制动转矩与制动角速度乘积的叠加[7]。在每个制动数据采集点，可使用瞬时制动转矩与制动角速度来计算摩擦耗能[8]：

在t=i时刻可测得转动惯量Im为：

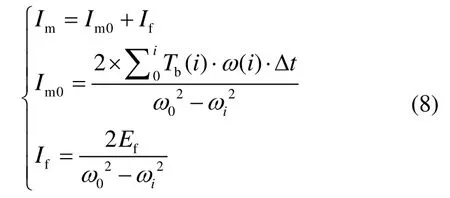
式中，If为系统阻力造成的惯量误差部分，Im0为根据转矩、角速度测量值计算得到的平均惯量部分。这样，系统阻力对模拟惯量的影响就被量化。同时，由式(8)可以看出，平均惯量Im0是与摩擦阻力无关的量，并且不受角加速度计算时滞的影响[9]，从而使这种方式计算得到的平均惯量可以作为控制的依据。为了弥补If对精度的影响，可利用Im0不受机械系统阻力影响这一特点，根据Im0与模拟目标惯量I作差，求解出惯量的偏差，再根据偏差的大小调节电机转矩。

在制动开始后的Δt时间后的每一个数据采集点，均可由式(8)及式(5)计算出Isima和Im0，其中，Δd=反映了惯量模拟的波动情况，反映了惯量模拟的精度偏差。Δe越小，受系统阻力影响就越小，惯量模拟精度越高，但并不代表惯量波动小；Δd越小，则惯量模拟的波动就较小，但也不能反映惯量模拟的精度。为了在控制瞬时模拟惯量波动的同时，控制惯量模拟的精度，就必须同时考虑平均惯量及瞬时模拟惯量相对于目标值的偏差，从而提出惯量偏差控制方程：

式中，α、β、γ为经验系数，i为数据采集点，Δdi为瞬时模拟惯量相对目标惯量的偏差，Δei为平均模拟惯量相对于目标惯量的偏差，Te(i)为电机输出转矩。

但是，式(9)存在以下问题：由图1可知，制动初始及终止时刻相对于制动期间，惯量模拟波动规律并不相同，不能使用单一的数学公式来模拟整个制动过程的电机转矩输出。又由式(5)可知，瞬时模拟惯量仅与制动转矩和制动角减速度的比值有关，在整个过程中难以建立电机的输出转矩与瞬时模拟惯量或平均模拟惯量的准确数学模型[10]，式(9)中的参数就难以确定。故，将式(9)改写为：

当平均模拟惯量偏差较大时，一般为制动初始阶段，为了避免产生较大的惯量累积误差，仅依据Δdi的大小来控制电机转矩。当平均惯量趋近模拟目标值,而瞬时惯量波动大时，根据Δt时间内瞬时惯量的累积偏差值确定控制量，控制惯量的波动。当瞬时模拟惯量和平均惯量的波动均在5 kg·m2以内时，系统采用开环控制，对Δt时间内惯量的偏差进行积分，逐步累积平均惯量偏差和瞬时模拟惯量偏差，在确保惯量精度的同时，维持较小的瞬时惯量波动，消除上下波动的惯量对输出信号的影响，从而减小模拟惯量的波动。当平均惯量偏差为负值时，电机输出固定的转矩。这样，在一个制动过程中，根据偏差的大小，分别以不同的控制策略输出电机转矩，则可解决控制方程参数难以确定的问题。

将t=i至t=i-Δt的一组原始制动转矩信号进行限幅平均滤波[11]，Δt取0.2 s，转矩限幅值为50 N·m。为了避免电机电流过大，需要对输出的控制量进行限制，故式(10)中其中TN为电机额定转矩。由于负惯量模式下，转矩输出受到制动机构结构的限制，本文仅针对正惯量进行讨论，

通过凑试法，首先仅调整α，将平均模拟惯量达到55

kg·m2时的α作为控制系数；再调整γ，将瞬时惯量偏差及平均模拟惯量偏差小于 5 kg·m2时的γ作为最终的控制系数，同时记录输出转矩值，计算调整β，记录不产生较大波动的β值。最终确定经验系数大小为：α=32，β=12，γ=0.5。

通过以上方法，直接根据惯量模拟偏差的大小，即系统阻力对惯量大小的影响程度来调整转矩输出，而且当制动转矩及机械振动对瞬时模拟惯量产生影响时，算法也可通过波动及偏差大小来进行调节。

4 惯量偏差控制算法的制动试验

采用惯量偏差控制算法设计测控软件的惯量模拟模块，进行制动试验，试验条件均与转矩控制法验证试验相同。

试验获得的瞬时模拟惯量曲线数据如图2所示。滤波方式与图1相同。

在图2中，对于惯量偏差控制方法模拟的瞬时惯量曲线，从整体曲线上看，总是围绕目标惯量波动。以两条垂直与制动时间轴的虚线为大致的界限，可看出：在阶段Ⅰ，忽略初始阶段的无效时间段，瞬时惯量曲线波动较大，在1 s内波动近20 kg·m2。在阶段Ⅱ，瞬时惯量偏差减小至5 kg·m2，并始终在目标惯量附近振荡；在阶段Ⅲ，惯量偏差控制法模拟的瞬时惯量波动小于5 kg·m2。相对而言，转矩控制法模拟的瞬时惯量在整个制动过程中的波动范围一直处于 5 kg·m2左右，但这个波动并没有以目标值为中心，波动中心与目标值的偏差随制动过程减小。

图2 惯量偏差控制法与转矩控制法瞬时模拟惯量对比Fig.2 Instantaneous simulation inertia in inertia deviation control method and torque control method

图2中惯量偏差控制法模拟的瞬时惯量曲线反映了控制算法对惯量波动的控制：在平均惯量偏离目标值较大的Ⅰ阶段，通过瞬时惯量的偏差迅速将平均惯量稳定在目标值附近；然后在阶段Ⅱ内，根据惯量的波动偏差及平均惯量偏差的累积来减小波动程度；在阶段Ⅲ内，在稳定偏差状态下转矩输出的基础上，依据平均偏差及瞬时偏差的累积值控制波动。由于转动惯量本身难以精确测量，阶段Ⅲ存在不可避免的波动。从整体曲线可看出，惯量偏差控制算法有效抑制了瞬时模拟惯量的波动。

为了验证惯量偏差控制法对惯量模拟精度的控制，重复进行六次试验，根据瞬时惯量数据，依照UIC548标准的平均惯量计算方法，得到平均模拟惯量的计算结果如表2所示。

表2 惯量偏差控制法平均模拟惯量及惯量模拟精度Tab.2 Average simulation inertia and simulation precision with inertia deviation control method

由表2可以看出：6次试验惯量模拟误差最小达到 0.62%，最大 4.94%，相较于转矩控制法最高精度提高了10.57%；试验1、3、4、5的标准差均小于3，说明瞬时惯量均在平均值附近波动，并且瞬时惯量偏差大于5 kg·m2的占比较转矩控制法小，但第2、6次试验标准差超过了9 kg·m2，这比转矩控制法高。

上述6次试验中，第2、6次试验的标准差较大，这是因为在制动初始阶段，瞬时惯量偏离目标值较大，系统对较大的偏差有明显的响应，存在超调，造成标准差偏大。但从平均模拟惯量可以看出，这种超调在一定程度上提高了惯量模拟精度，使得这两次试验的惯量模拟精度都比其他试验高，这是由于电机、惯量盘等转动系统对较小的转矩响应并不明显。当偏差较大时，在固定的积分区间Δt内，平均惯量偏差累积值就更大，电机转矩响应就比较明显，从而使平均惯量接近目标值，模拟精度就更高。同时第一、三、五次试验也证明了这点，在Δei较小的情况下，累积偏差值产生的作用就较小，转矩响应并不明显，使得偏差无法彻底消除，故精度相比偏差较大的情况降低了1%～2%。

转动系统的固有阻力通过影响转动的角减速度使惯量模拟值偏小。而惯量偏差控制法把惯量偏差Δd及Δe作为控制的依据，当Δd为正值，即瞬时模拟值较小，则电机应输出较大转矩，从而提高瞬时惯量减小偏差，故可以弥补机械阻力造成的影响。

5 结 论

1）转矩控制算法模拟电惯量时，难以精确考虑机械系统固有阻力的影响，由于机械阻力的存在，会使所测制动角减速度偏大，从而造成惯量模拟结果低于目标值，同时摩擦材料性能的变化、角减速度的计算时滞、机械振动因素都会对模拟惯量产生影响。

2）基于摩擦制动能量方程，提出了依据瞬时模拟惯量及平均模拟惯量与目标惯量偏差大小的惯量偏差控制方法，这种控制方法直接依据惯量模拟的偏差计算电机转矩输出量，控制瞬时模拟惯量的波动，可修正摩擦材料性能的变化、角减速度的计算时滞、机械振动等因素对惯量波动的影响，同时，避免了机械转动系统阻力对惯量模拟精度的影响。

3）所提出的惯量偏差控制方法考虑了基于不同偏差大小的电机转矩输出策略。模拟惯量偏差较大时采用比例控制方式，在惯量偏差较小时，采用逐渐累积平均模拟偏差及瞬时模拟偏差的调整方法。

4）相较于转矩控制法，惯量偏差控制法瞬时模拟惯量波动大于5 kg·m2的时间减少了60%，惯量模拟的精度提高了约10%。

参考文献（References）：

[1]莫志勇, 张为公, 吉同舟. 汽车机械惯量电模拟技术[J]. 中国惯性技术学报, 2009, 17(1): 123-126.Mo Z Y, Zhang W G, Ji T Z. Electrical simulation of vehicle mechanical inertia[J]. Journal of Chinese Inertial Technology, 2009, 17(1): 123-126.

[2]Ma J J, Wu B D, Sun X Y, et al. Compensation of inertia error in brake dynamometer testing[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2010, 224(3): 355-359.

[3]Fajri P, Ahmadi R, Ferdowsi M. Test bench for emulating electric-drive vehicle systems using equivalent vehicle rotational inertia[C]//Power and Energy Conference at Illinois (PECI). 2013: 83-87.

[4]宫文斌, 刘安龙, 江阔, 等. 机械惯量混合电模拟技术研究[J]. 农业机械学报, 2009, 40(1): 208-212.Gong W B, Liu A L, Jiang K, et al. Research on the technique of mechanical inertia mix electric simulation[J].Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(1): 208-212

[5]王皖君, 张为公, 李旭. 变速器试验台惯量电模拟与角加速度估计[J]. 东南大学学报(自然科学版), 2012,42(1): 62-66.Wang W J, Zhang W G, Li X. Inertia electrical emulation and angular acceleration estimation for transmission test rig[J]. Journal of Southeast University (Natural Science Edition). 2012. 42(1): 62-66.

[6]刘和平, 战祥真, 李红新, 等. 惯量自补偿的纯电动汽车动力系统模拟试验台研究[J]. 电机与控制学报,2011, 15(10): 55-62.Liu H P, Zhan X Z, Li H X, et al. Research on selfcompensated inertia test rig of pure electric vehicle dynamic system[J]. Electric Machines and Control, 2011,15(10): 55-62.

[7]Lee S, Dong X, Wang K D. Research on electric simulation of mechanical inertia in an inertia brake dynamometer[C]//Proceedings of 2015 IEEE International Conference on Mechatronics and Automation. 2015: 1326-1331.

[8]Zhang L X, Li P. A novel control method of brake test bench[C]//World Automation Congress Proceedings.Mexico, 2012: 141-143.

[9]Ji X W, Sun N, Ge J G, et al. Inertia compensation based on torque signal in an electric power steering system[C]//Proceedings of the FISITA 2012 World Automotive Congress. 2013: 761-768.

[10]盛朝强, 谢昭莉. 基于电惯量的汽车惯性式制动试验系统的设计[J]. 重庆大学学报(自然科学版), 2005,28(1): 90-92.Sheng C Q, Xie Z L. Design of automobile-inertia-braketesting-system based on electrical-inertia[J]. Journal of Chongqing University (Natural Science Edition), 2005,28(1): 90-92.

[11]Shafi S, Kumar S V, Sengolrajan T. Pressure and torque control in brake inertia dynamometer[C]//International Conference on Innovations in Information Embedded and Communication Systems. Coimbatore, India, 2015: 1-5.