三阶不可约零-非零模式中的几乎惯量任意模式

续晓欣，高玉斌，梁月亮

（1.中北大学 仪器与电子学院，山西 太原030051；2.中北大学 理学院，山西 太原030051）

近年来，关于符号模式（或零-非零不可约模式）的惯量任意性与惯量临界集（或精细惯量任意性与精细惯量临界集）的研究成果很多.文献［1］根据惯量临界集的定义，给出并验证了n=2，3，4时不可约零-非零模式的极小惯量临界集以及n=2，3时不可约符号模式的极小惯量临界集.文献［2］阐述了精细惯量的定义并得出：n≤3时不可约零-非零模式的惯量任意性、精细惯量任意性与谱任意性是等价的，当n=4时不可约零-非零模式的精细惯量任意性与谱任意性是等价的，而对于更高阶的不可约零-非零模式，上述结论则不一定成立.文献［3］利用组合矩阵论的方法，得到并验证了n=2，3时不可约零-非零模式的所有极小惯量临界集以及所有极小精细惯量临界集.在文献［4］中，二阶不可约符号模式的所有极小精细惯量临界集都得到了验证.对于任意蕴含幂零的全符号模式，文献［5］证明其一定是谱任意（从而也是惯量任意）的.最近，文献［6］给出并验证了三阶全符号模式的所有极小精细惯量临界集，从而使惯量临界集（精细惯量临界集）的研究开辟到全符号模式的领域.

几乎惯量任意的不可约零-非零模式是2010年文献［7］中提出的一个概念，文献［7］的引理2.3证明了三阶不可约零-非零模式M蕴含除（0，0，3）之外其余所有可能的惯量，称此时的不可约零-非零模式M是几乎惯量任意的.国内关于几乎惯量任意模式的研究只限于符号模式矩阵的范畴，杨正民等人在文献［8］中证明了一类符号模式是几乎完全惯量任意的符号模式，梅银珍等人在文献［9］中利用矩阵的直和构造出一种几乎完全惯量任意的符号模式矩阵.目前，国内外针对几乎惯量任意的不可约零-非零模式的系统研究尚未展开.本文在深入研究不可约零-非零模式的基本概念和基础理论之后，受文献［7］启发，探讨三阶不可约零-非零模式中的几乎惯量任意的模式，将三阶不可约零-非零模式按照惯量任意模式、几乎惯量任意模式、非惯量任意又非几乎惯量任意模式分为三类，并对其进行了归类研究.

一般说来，验证符号模式是惯量任意的，可以采取一些常规的方法，比如：幂零-雅可比方法、幂零-中心化方法［10］，对于不可约零-非零模式，没有常规的方法可以验证其惯量任意性.因此，本文采用分析法与列举法结合的方法得到三阶不可约零-非零模式中几乎惯量任意的所有模式M，N，P.首先，利用组合理论中矩阵迹与特征值的关系以及矩阵特征多项式与特征值的关系，证明（0，0，3）不能被以上三种模式蕴含；其次，对于每一个除（0，0，3）之外的三阶零-非零模式的惯量，给出每个惯量在实数域上具体的矩阵实现，说明M，N，P蕴含这个惯量，从而证明三种模式M，N，P是几乎惯量任意的.

1 预备知识

首先介绍零-非零模式的相关概念.零-非零模式矩阵是指元素取自集合｛＊，0｝的矩阵，其中＊指的是任意的非零实数.若零-非零模式矩阵A（以下简称模式）通过转置及置换相似的有限次组合变换可以得到模式B，则称模式A与B模式等价.若B=A或者将A中的一个或多个非零元素替换为零元素后可以得到模式B，则称模式B为模式A的一个子模式，同时A为B的一个母模式.若模式A置换相似于模式其中A11，A12为非空方阵，则称模式A为可约的，否则称A为一个不可约模式.具有相同模式A的n阶实矩阵全体称为模式A的定性矩阵类.模式A的谱是指该模式的所有定性类矩阵的特征值组成的集合.

n阶实矩阵A的惯量是指满足n++n-+n0=n的三元有序数组（n+，n-，n0），其中n+，n-，n0分别为矩阵A的具有正实部、负实部和零实部的特征值的个数［11］.模式A蕴含惯量（n+，n-，n0）是指，在模式A的定性矩阵类中至少存在一个实矩阵具有这样的惯量.事实上，模式A蕴含惯量（n+，n-，n0）当且仅当A蕴含惯量（n-，n+，n0），这是由于，若矩阵A属于某个模式的定性矩阵类中，则-A亦属于这个定性矩阵类中，称以上两种惯量互为彼此的反转惯量［1］.若模式A蕴含所有可能的惯量，则称模式A是惯量任意的，若模式A蕴含除某个惯量之外的其余所有惯量，则称模式A是几乎惯量任意的.

n阶实矩阵A的精细惯量是指满足n++n-+nz+2np=n的四元有序数组（n+，n-，nz，2np），其中，nz为矩阵A零特征值个数，2np是指A纯虚数特征值的个数［2，12］.模式A蕴含精细惯量（n+，n-，nz，2np）是指，在模式A的定性矩阵类中存在至少一个实矩阵具有（n+，n-，nz，2np）这样的精细惯量.若模式A蕴含所有可能的精细惯量，则称模式A是精细惯量任意的，若模式A蕴含除某个精细惯量之外的其余所有精细惯量，称模式A是几乎精细惯量任意的.类似于惯量的性质，模式A蕴含精细惯量（n+，n-，nz，2np）当且仅当A蕴含精细惯量（n+，n-，nz，2np），称以上两种精细惯量互为彼此的反转精细惯量［2］.设S为n阶模式所有惯量构成集合的一个非空真子集，对于任意的n阶零-非零模式A，若集合S⊆i（A）可以使得该n阶零-非零模式A惯量任意，则称S是n阶零-非零模式的一个惯量临界集.类似可以得到精细惯量临界集的定义.

接下来列出本文主要证明中所需的三阶模式的基本性质：

引理1［3］设A为三阶不可约零-非零模式，则其对应的关联有向图中含有一个三圈或两个二圈.

引理2［7］设A为三阶不可约零-非零模式，则A为惯量任意当且仅当A对应的关联有向图中含有子图B，其中B中含有至少两个环、两个三阶置换有向图以及至少一个二圈.

引理3［13］设A为三阶不可约零-非零模式，则A满足以下结论：

1）若A含有5个或5个以下的非零元素，则A不是谱任意的；

2）若A含有6个非零元素且是谱任意的，则A是极小谱任意的并且等价于以下两种形式之一

3）若A含有7个或7个以上非零元素并且主对角线至少2个非零元素，则A是谱任意的，但不是极小谱任意.

三阶模式的谱任意性与惯量任意性是等价的［2］，因此将上述引理3中的谱替换为惯量，结论同样成立.

引理4［14］若模式A为惯量任意的三阶不可约零-非零模式，则模式A必等价于以下两种模式之一的母模式

2 主要结论

根据引理1，所有三阶不可约零-非零模式（对应的关联有向图为强连通图）共有25种情形（在等价意义下），下面将三阶不可约零-非零模式分为惯量任意模式、几乎惯量任意模式、非惯量任意又非几乎惯量任意模式三种情形分别进行讨论.

2.1 惯量任意的三阶模式

根据引理4，惯量任意的三阶模式共有9种，它们分别是

D1的母模式

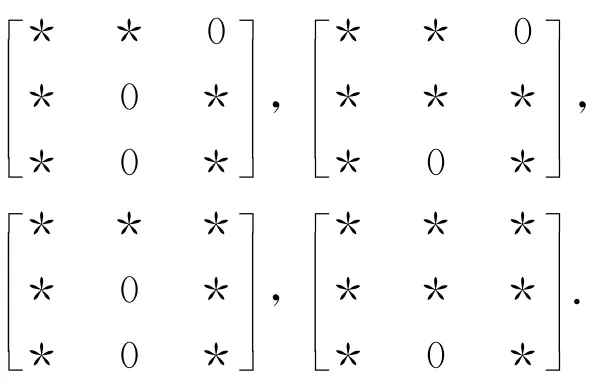
D2的母模式

2.2 几乎惯量任意的三阶模式

三阶模式中几乎惯量任意的模式共有3种，下面给出与几乎惯量任意模式有关的4个命题及3个推论，并逐一证明.

命题1 三阶模式

是几乎惯量任意的，即蕴含除（0，0，3）之外的其余所有惯量.

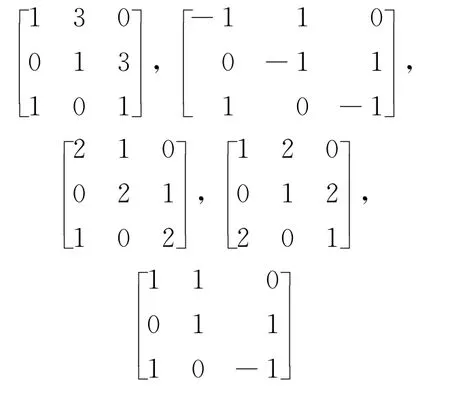
证明 根据文献［3］中不可约零-非零模式惯量个数的计算公式三阶模式共有10种惯量.由于模式M对应的关联有向图中不含有二圈，根据引理2结论，模式M不是惯量任意的.下面说明模式M是几乎惯量任意的.考虑模式M在实数域上的5个矩阵实现，矩阵分别取到惯量（1，2，0），（0，2，1），（3，0，0），（1，0，2），（1，1，1）.注意到一个模式蕴含惯量（n+，n-，n0）当且仅当其蕴含惯量（n-，n+，n0），将以上前4个实矩阵分别取负矩阵，则这4个负矩阵分别取到惯量（2，1，0），（2，0，1），（0，3，0），（0，1，2）.至此，模式M蕴含9个惯量，分别为（1，2，0），（0，2，1），（3，0，0），（1，0，2），（1，1，1），（2，1，0），（2，0，1），（0，3，0）与（0，1，2），由于模式M不是惯量任意的，则M不能蕴含惯量（0，0，3）.因此，模式M是几乎惯量任意的.

命题2 三阶模式

是几乎惯量任意的，即蕴含除（0，0，3）之外的其余所有惯量.

证明 从矩阵模式N的结构可以看出，模式N对应的关联有向图中只有一个环，根据引理2结论可知，模式N不是惯量任意的.又根据组合矩阵论的知识可知，矩阵模式N的迹是非零的，亦即模式N定性矩阵类中的任意矩阵其特征值之和非零，因此，模式N不能蕴含惯量（0，0，3），下面说明模式N蕴含其余所有的惯量，考虑模式N实数域上的5个矩阵实现，矩阵

分别取到惯量（1，2，0），（1，1，1），（1，0，2），（2，0，1）与（3，0，0），由于一个模式蕴含惯量（n+，n-，n0）当且仅当其蕴含惯量（n-，n+，n0），则模式N同样蕴含惯量（2，1，0），（0，1，2），（0，2，1）与（0，3，0），因此，模式N蕴含除（0，0，3）之外的其余所有惯量，即模式N是几乎惯量任意的.

命题3 三阶模式

是几乎惯量任意的，即蕴含除（0，0，3）之外的其余所有惯量.

证明 由于（0，0，3）∈i（P）当且仅当i（P）蕴含形如x3+qx（q≥0）的特征多项式.假设矩阵A是模式P的一个实数域矩阵实现，不失一般性，设其中a，b，c，d是任意的非零实数.此时，矩阵A的特征多项式为

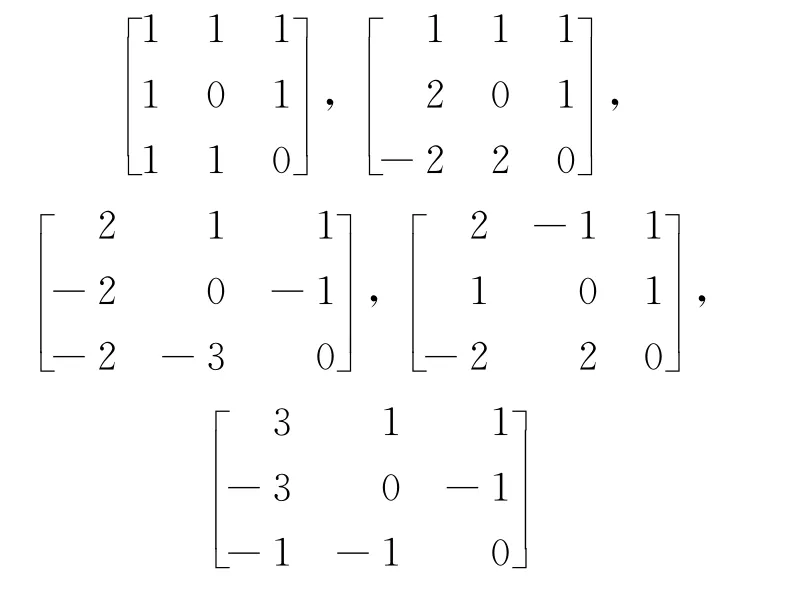
假设pA（x）=x3+qx，则a=0，与假设a是非零实数矛盾.因此，i（P）不能蕴含形如x3+qx（q≥0）的特征多项式，于是模式P不能蕴含惯量（0，0，3）.下面考虑模式P实数域上的5个矩阵实现，矩阵

分别取到惯量（1，0，2），（1，1，1），（2，0，1），（3，0，0）与（2，1，0）.因此，模式P同样蕴含惯量（0，1，2），（0，2，1），（0，3，0）与（1，2，0），综上可知模式P蕴含除（0，0，3）之外的其余所有惯量，即模式P是几乎惯量任意的.

推论1［7］设集合S是三阶不可约零-非零模式的一个惯量临界集，则（0，0，3）∈S.

证明 根据命题1，命题2及命题3可知，模式M，N与P均为几乎惯量任意零-非零模式，即蕴含除（0，0，3）之外的其余所有惯量，用反证法证明推论1成立，设S是三阶模式的一个惯量临界集并且（0，0，3）不属于S，则S必包含三阶模式惯量集合中的其它惯量，此时有S∈i（M），S∈i（N）及S∈i（P）成立.根据惯量临界集的定义，若模式蕴含临界集S中的惯量，则模式必蕴含所有可能的惯量，亦即该模式是惯量任意的，而命题1，命题2与命题3分别指出M，N与P均不是惯量任意的，这与S是三阶模式惯量临界集并且（0，0，3）∉S的假设矛盾.因此，若S为三阶不可约零-非零模式的惯量临界集，则（0，0，3）∈S.

结合命题1，命题2，命题3及惯量与精细惯量的关系可得以下推论：

推论2 三阶模式

均不蕴含精细惯量（0，0，1，2）与（0，0，3，0）.

命题4 三阶模式

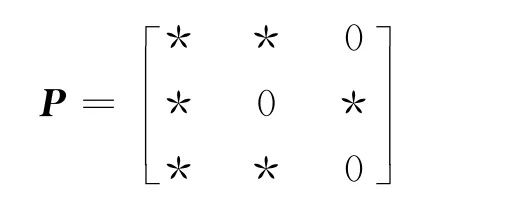
蕴含除（0，0，1，2）与（0，0，3，0）之外的其余所有精细惯量.

证明 根据文献［2］定理1.1中精细惯量个数的计算公式可知，三阶模式的精细惯量共有8种（互为反转精细惯量的一对精细惯量视为等价的1种精细惯量），由命题3可知，模式P不能蕴含惯量（0，0，3），因此一定不能蕴含精细惯量（0，0，1，2）与（0，0，3，0），下面说明模式P蕴含其余6种精细惯量，考虑模式P实数域上的6个矩阵实现，事实上，下列矩阵

分别取到精细惯量（1，0，0，2），（1，0，2，0），（1，1，1，0），（2，0，1，0），（3，0，0，0）与（2，1，0，0）.因此，模式P蕴含除（0，0，1，2）及（0，0，3，0）之外的其余所有精细惯量.

推论3 设集合S′为三阶模式的一个精细惯量临界集，则S′包含（0，0，3，0）或（0，0，1，2）.

证明 利用反证法获证.假设（0，0，3，0）与（0，0，1，2）均不属于S′，则S′中必定包含三阶模式精细惯量集合中的其它精细惯量，由推论2可知，模式M，N与P均不是精细惯量任意的.与S′为三阶模式精细惯量临界集的定义矛盾.

2.3 非惯量任意又非几乎惯量任意的三阶模式

根据引理3中（1），非零元素为5个或5个以下的三阶模式不是谱任意的，从而不是惯量任意的.下面说明这些模式也不是几乎惯量任意的.

2.3.1 非零元素为3个的三阶模式有1种：

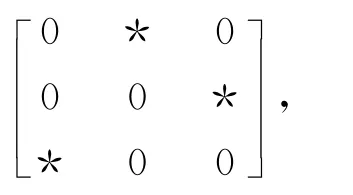
此模式要求非奇异且迹为零.因此，给定的三阶模式不能蕴含惯量（0，2，1），（2，0，1），（0，0，3），（1，1，1），（3，0，0），（0，3，0），（1，0，2）及（0，1，2）.

从而可知此三阶模式不是几乎惯量任意的.2.3.2 非零元素为4个的三阶模式有3种：

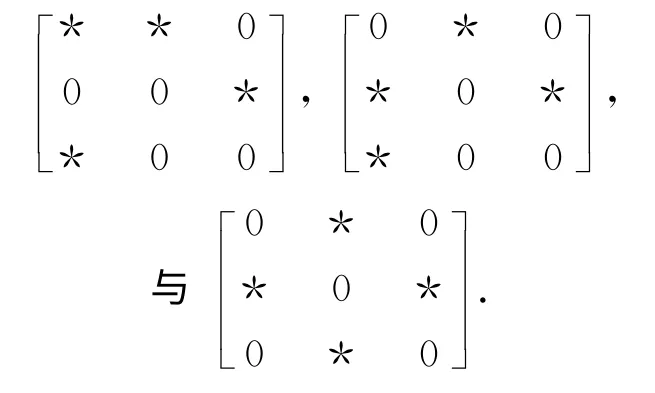
第一种模式要求非奇异且迹非零，因此不能蕴含惯量（0，2，1），（2，0，1），（0，0，3）与（1，1，1）；第二种模式要求非奇异且迹为零，因此不能蕴含惯量（0，2，1），（2，0，1），（0，0，3），（1，1，1），（3，0，0），（0，3，0），（1，0，2）与（0，1，2）；第三种模式要求奇异且迹为零，因此不能蕴含惯量（0，2，1），（2，0，1），（2，1，0），（1，2，0），（3，0，0），（0，3，0），（1，0，2）与（0，1，2）.综上可知这3种模式不是几乎惯量任意的.

2.3.3 非零元素为5个的三阶模式有5种：

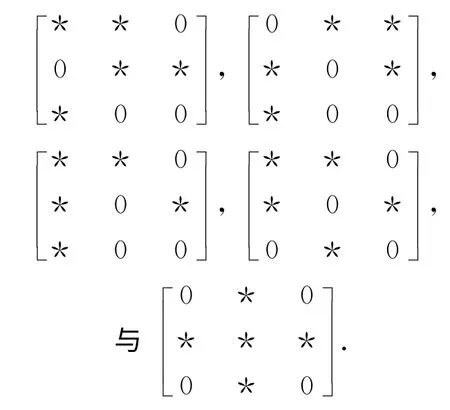
第一种模式要求非奇异，因此不能蕴含（0，2，1），（2，0，1），（0，0，3），（1，1，1）；第二种模式要求非奇异且迹为零，因此不能蕴含惯量（0，2，1），（2，0，1），（0，0，3），（1，1，1），（3，0，0），（0，3，0），（1，0，2）与（0，1，2）；第三种、第四种模式要求非奇异且迹非零，因此不能蕴含惯量（0，0，3），（1，1，1），（0，2，1），（2，0，1）；第五种模式要求奇异且迹非零，因此不能蕴含惯量（3，0，0），（0，3，0），（2，1，0），（1，2，0），（0，0，3）.综上可知上述5种模式均不是几乎惯量任意的.

由以上分析可知，非零元素为5个或5个以下的三阶模式均不是惯量任意的，同时也不是几乎惯量任意的.

2.3.4 非零元素为6个的模式有4种：

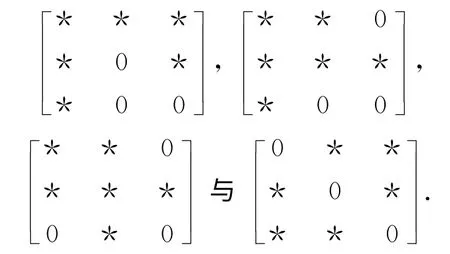
第一种模式要求非奇异且迹非零，因此不能蕴含惯量（0，0，3），（1，1，1），（0，2，1）与（2，0，1）；第二种和第三种模式要求非奇异，因此不能蕴含惯量（0，2，1），（2，0，1），（0，0，3）与（1，1，1）；第四种模式要求迹为零，则不能蕴含惯量（3，0，0），（0，3，0），（0，2，1），（2，0，1），（1，0，2）与（0，1，2）.由此可得这4种模式均不是惯量任意的，也不是几乎惯量任意的.

结合2.1，2.2及2.3可知，三阶模式中，惯量任意的模式有9种，分别是

几乎惯量任意的模式有3种，具体为

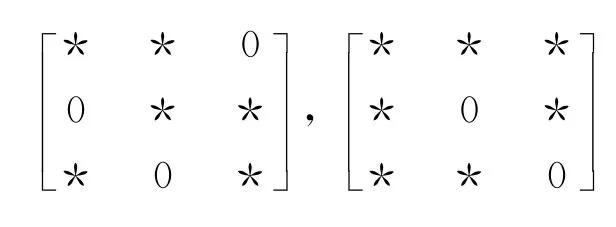
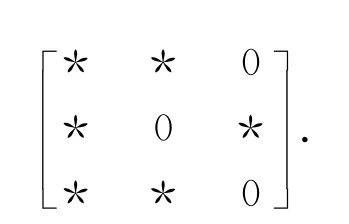
既非惯量任意又非几乎惯量任意的模式有13种，分别为

3 结束语

文中对三阶不可约零-非零模式的所有情形（在等价意义下共25种）进行了分类讨论：列出了惯量任意模式，共9种，得到了所有的几乎惯量任意模式，共3种，同时得到非惯量任意又非几乎惯量任意的模式，共13种.进一步验证了集合作为三阶模式惯量临界集的必要条件.给出集合作为三阶模式精细惯量临界集的一个必要条件.事实上，关于几乎惯量任意的零-非零模式尚有许多性质有待进一步探讨.譬如，惯量任意零-非零模式与几乎惯量任意零-非零模式之间的关系、零-非零模式是几乎惯量任意零-非零模式的充分或必要条件等.

［1］Kim I J，Olesky D D，van den Driessche P.Critical sets of inertias for matrix patterns［J］.Linear and Multilinear Algebra，2009，57（3）：293-306.

［2］Deaett L，Olesky D D，van den Driessche P.Refined inertially and spectrally arbitrary zero-nonzero patterns［J］.Electron.J.Linear Algebra，2010，20：449-467.

［3］Yu Berlin，Huang Hingzhu，Hua Hongbo.Critical sets of refined inertias for irreducible zero-nonzero patterns of order 2 and 3［J］.Linear Algebra and its Application，2012，437：490-498.

［4］Yu Berlin.Minimal critical sets of refined inertias for irreducible sign patterns of order 2［J］.Adv，Linear Algebra Matrix Theory，2013（3）：7-10.

［5］Pereira R J.Nilpotent matrices and spectrally arbitrary sign patterns［J］.Electron.J.Linear Algebra，2007，16：232-236.

［6］Gao Wei，Li Zhongshan，Zhang Lihua.The minimal critical sets of refined inertias forfull sign patterns［J］.Linear Algebra and its Application，2014，458：183-196.

［7］Yu Berlin，Huang Tingzhu.Minimal critical sets of inertias for irreducible zero-nonzero patterns of order 3［J］.International Journal of Mathematical ffComputer Sciences，2010，6（4）：189-191.

［8］杨正民，胡红萍，高玉斌.几乎完全惯量任意符号模式［J］.华北工学院学报，2003，24（5）：346-349.Yang Zhengmin，Hu Hongping，Gao Yubin.Almost inertially arbitary pattern［J］.Journal of North China Institute of Technology，2003，24（5）：346-349.（in Chinese）

［9］梅银珍，王鹏，陈淑琴.几类特殊的谱任意和惯量任意符号模式矩阵［J］.中北大学学报（自然科学版），2009，30（4）：307-311.Mei Yinzhen，Wang Peng，Chen Shuqin.Some spectrally and inertially arbitrary sign patterns［J］.Journal of North University of China（Natural Science Edition），2009，30（4）：307-311.（in Chinese）

［10］Cavers M S，Garnett C，Kim I J，et al.Techniques for identifying inertially arbitrary patterns［J］.Electron.J.Linear Algebra，2013，26：71-89.

［11］Horn R A，Johnson C R.Matrix Analysis［M］.New York：Cambridge University Press，1985.

［12］Kim I J，Olesky D D，Shader B L，et al.Generating potentially nilpotent full sign patterns［J］.Electron.J.Linear Algebra，2009，18：162-175.

［13］Corpuz L，Mcdonald J J.Spectrally arbitrary zerononzero patterns of order 4［J］.Linear and Multilinear Algebra，2007，55（3）：249-273.

［14］Cavers M S，Vander Meulen K N.Inertially arbitrary nonzero patterns of order 4［J］.Electron.J.Linear Algebra，2007，16：30-43.