对心直动平底从动件运动规律的研究
2020-08-25刘建强邓帅卿
刘建强,邓帅卿,杨 彪
(太原理工大学 机械与运载工程学院,山西 太原 030024)
0 引言
对心直动平底从动件盘形凸轮机构在工程上的应用较为广泛,在已知凸轮轮廓列表曲线的情况下对从动件运动规律进行研究具有重大意义。然而,目前国内外对这方面的研究较少且已有的研究较为复杂。在该背景下,本文基于三点作圆圆弧逼近列表曲线法并巧妙地运用几何关系,给出了对心直动平底从动件盘形凸轮机构从动件运动规律的较为简单的求解方法。最后给出了通过MATLAB对从动件运动规律进行求解的实例。
1 列表曲线处曲率中心与曲率半径的近似求解
当已知列表曲线时,即已知曲线上某些坐标点但没有给出方程的曲线,可以通过三点作圆圆弧逼近列表曲线的方法,求出列表曲线处曲率中心的坐标及曲率半径。下面给出三点作圆圆弧逼近列表曲线方法。
如图1所示,Q1、Q2、Q3、Q4、Q5、Q6为列表曲线上的点,O1、R1分别为过Q1、Q2、Q3三点所做圆弧的圆心与半径,即Q1、Q2、Q3点处的曲率中心与曲率半径。
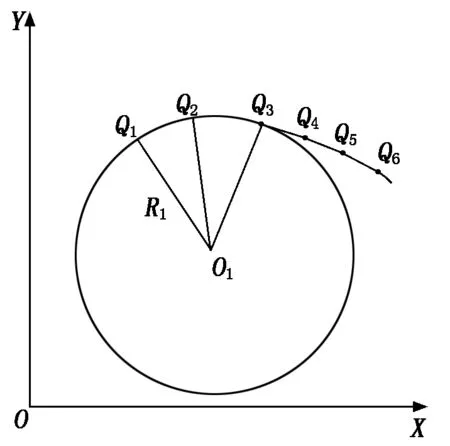
图1 三点作圆圆弧逼近列表曲线法原理图
设(X1,Y1)、(X2,Y2)与(X3,Y3)分别为Q1、Q2、Q3点处对应的坐标,(X1′,Y1′)与(X2′,Y2′)分别为Q1与Q2中点坐标及Q2与Q3中点坐标,(X0,Y0)为圆心坐标。则:
(1)
Y0=K1(X0-X1′)+Y1′.
(2)
(3)
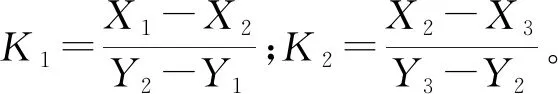
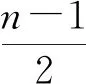
2 根据几何关系求解从动件运动规律
如图2所示为一对心直动平底从动件盘形凸轮机构,其平底与从动件导路中心线垂直。以凸轮回转中心O为原点,以通过凸轮对称轴并指向凸轮近休止处外法线方向建立OX轴,在OX轴逆时针旋转90°方向建立OY轴,凸轮基圆半径为Rb。
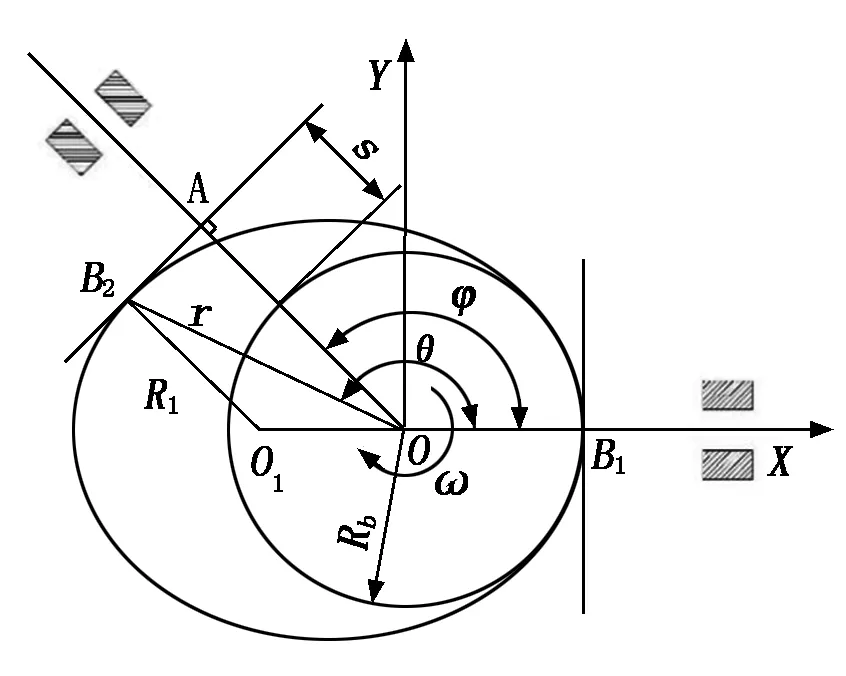
图2 对心直动平底从动件盘形凸轮机构
凸轮以等角速度ω沿顺时针方向转动,根据“反转法”原理,从动件绕O点以等角速度-ω转过φ角时,其对应的位移为s。此时,平底与凸轮的接触点由B1变为B2。图2中,θ与r分别为凸轮上B2点处对应的极角与极径,O1与R1分别为B2点处对应的曲率中心和曲率半径。
根据几何关系,在△OB2O1中运用余弦定理可得:
(4)
在直角△AOB2中有:
(5)
又OA//B2O1,则∠OB2O1=∠AOB2=θ-φ,则:
(6)
化简得:
(7)
(8)
式(7)中,Rb已知,则对于给定的列表曲线r=r(θ),可根据上述三点作圆圆弧逼近列表曲线法求出从动件运动规律对应的列表曲线s=s(φ)。
3 通过MATLAB求解从动件运动规律计算实例
表1是凸轮上部分点所对应的极坐标系下的坐标值以及通过计算得到的各点对应的直角坐标系下的坐标值。
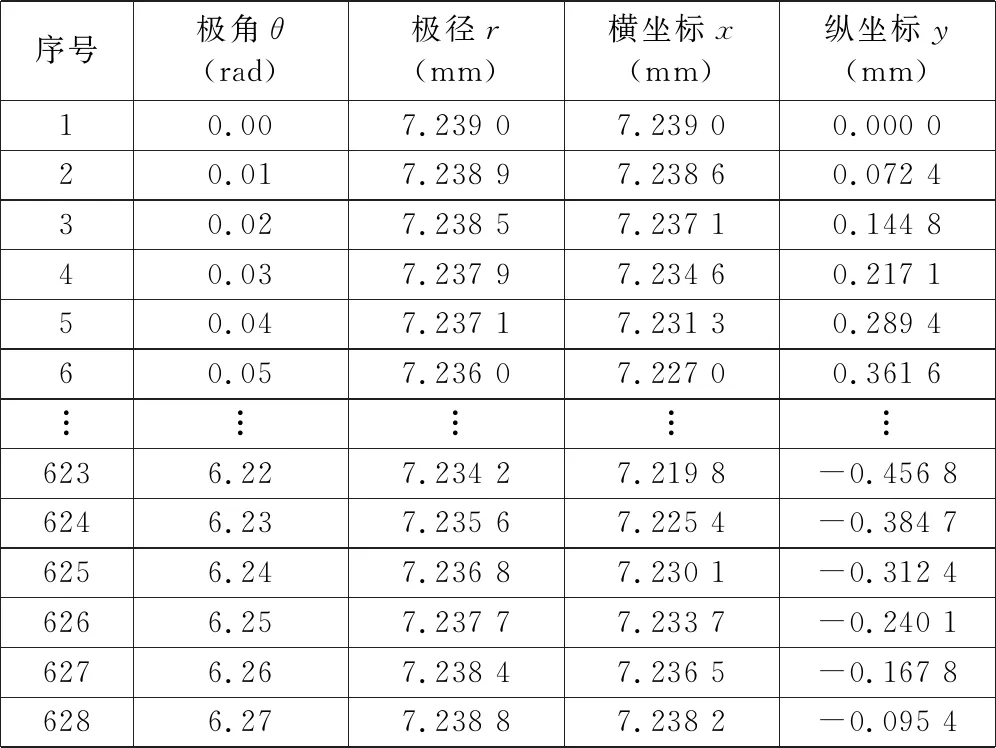
表1 极坐标系下与直角坐标系下凸轮部分点的坐标值
MATLAB求解代码如下:
clc,clear
x=xlsread('C:UsersAdministratorDesktopA-20191','D2:D629');%每个极径极角对应的x坐标
y=xlsread('C:UsersAdministratorDesktopA-20191','E2:E629');%每个极径极角对应的y坐标
Rb=2.413;%基圆半径
r=xlsread('C:UsersAdministratorDesktopA-20191','B2:B629');%导入极径
v=xlsread('C:UsersAdministratorDesktopA-20191','A2:A629');%导入极角
for i=1∶2∶626;
X5=(x(i)+x(i+1))/2;Y5=(y(i)+y(i+1))/2;
X6=(x(i+1)+x(i+2))/2;Y6=(y(i+1)+y(i+2))/2;
K1=(x(i)-x(i+1))/(y(i+1)-y(i));
K2=(x(i+1)-x(i+2))/(y(i+2)-y(i+1));
Ox((i+1)/2)=((K2*X6)-(K1*X5)+(Y5-Y6))/(K2-K1);%圆心横坐标
Oy((i+1)/2)=K1*(Ox((i+1)/2)-J5)+Y5;%圆心纵坐标
R((i+1)/2)=sqrt((x(i)-Ox((i+1)/2))^2+(y(i)-Oy((i+1)/2))^2);%圆心到切点距离
RO((i+1)/2)=sqrt(Ox((i+1)/2)^2+Oy((i+1)/2)^2);%圆心到原点距离
s((i+1)/2)=((RO((i+1)/2))^2+r(i)^2+(R((i+1)/2))^2)/(2*R((i+1)/2))-Rb;%由几何关系求推程
e((i+1)/2)=acos(((RO((i+1)/2))^2+r(i)^2+R((i+1)/2)^2)/(2*R((i+1)/2)*r(i)));%由几何关系求极角与转角的差值
b((i+1)/2)=v(i)-e((i+1)/2);%求转角
end
for i=2∶313
if abs(s(i)-s(i-1))>1
s(i)=s(i-1);
b(i)=b(i-1);
end
end
plot(b,s,'+r')
title('凸轮从动件位移与凸轮转角的关系')
xlabel('凸轮转角/rad')
ylabel('从动件位移')
通过上述代码求得的从动件运动规律如图3所示。
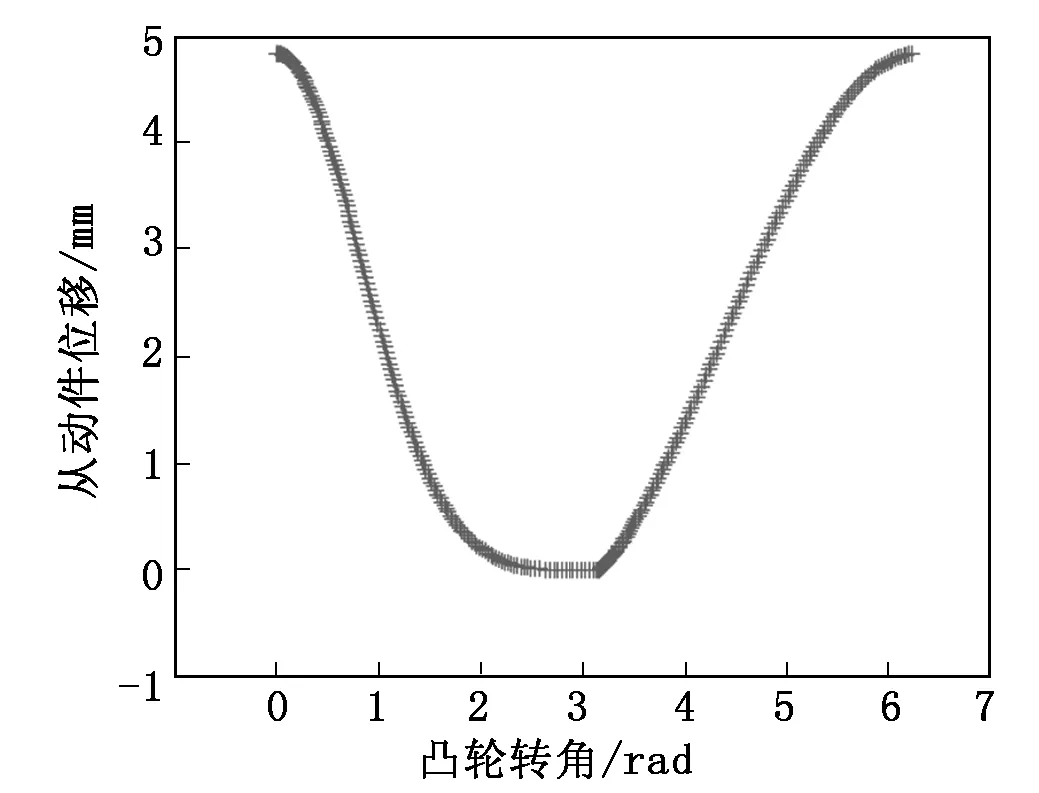
图3 从动件运动规律
4 结语
本文基于三点作圆圆弧逼近列表曲线法并巧妙地运用几何关系,给出了求解对心直动平底从动件盘形凸轮机构从动件运动规律的较为简单的方法。在此基础上,给出了通过MATLAB求解从动件运动规律的代码,对该类问题的求解具有借鉴意义。
