基于Lagrange方程和二阶影响系数矩阵的Delta并联机构约束力分析及仿真研究*
2021-08-06郭志飞甄希金张敬芳
张 勇,郭志飞*,甄希金,张敬芳
(1.河北机电职业技术学院 机械工程系,河北 邢台 054001;2.上海船舶工艺研究所,上海 200032)
0 引 言
并联机构具有刚度好、运动精度高、易在线控制等优点,在许多工业领域的应用广泛[1]。对其进行动力学分析对于并联机构的结构设计、动力学性能优化和实时控制都具有重要的意义[2]6-7。
对并联机构的动力学分析需要系统的方法[2]119,并联机构的力学分析也是并联机构研究的基本问题[3-5]。目前,国内外在并联机构动力学分析方面取得了较大的成果,常用的并联机构动力学分析方法有Lagrange方法、Newton-Euler法和Kane方法[6-7]。YANG D C H[8]利用Newton-Euler法研究了Stewart平台的逆动力学问题;但该研究忽略了关节的摩擦和杆的力矩惯量,并且其假设杆的中心位于杆的轴线上。JI Zhi-ming[9]在1994年建立了Stewart平台的动力学方程,并且该方程考虑了腿部转动惯量对Stewart平台的影响。CODOUREY A[10]介绍了基于拉格朗日方程和虚功原理的并联机构动力学建模方法,其中Lagrange方法是以能量为基础建立的动力学的数学模型,该方法能够得到形式简洁的动力学方程,十分适用于并联机构的动力学分析[11];但是,该方法的不足之处是其无法进行约束力分析,Kane方法亦然。在多数情况下,Newton-Euler法被用于对并联机构的约束力进行分析研究,但其过程复杂、方程数量庞大、易出错[12,13]。
综上,本文开展基于逆动力学的并联机构约束力的分析研究,通过建立三平移Delta并联机构的Lagrange动力学模型,使用二阶影响系数矩阵求解滑块的加速度,对三平移Delta并联机构驱动滑块的约束力进行分析和求解,为三平移Delta并联机构结构设计及控制系统设计提供理论依据。
1 Lagrange动力学模型建立
本文所研究的三平移动Delta并联机构如图1所示。
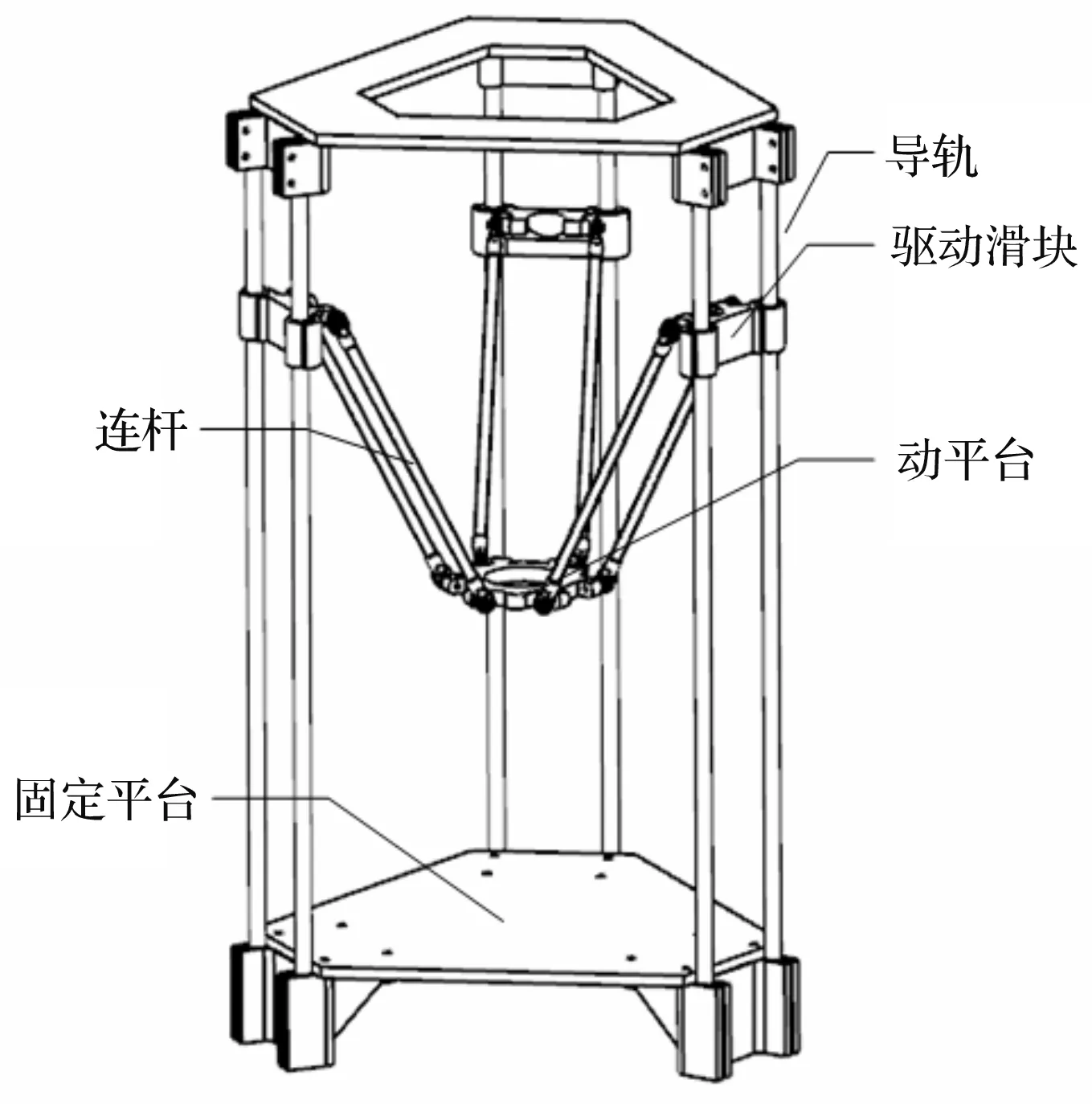
图1 三平移Delta并联机构
图1中,该并联机构的主要组成部分有:固定平台、导轨、滑块、连杆、动平台等。当3个滑块以不同规律运动的时候,动平台就可以实现沿X、Y、Z方向的平动,以及各种耦合形式的运动。
为了便于后续分析,笔者将该并联机构进行简化,机构位置结构简图如图2所示。
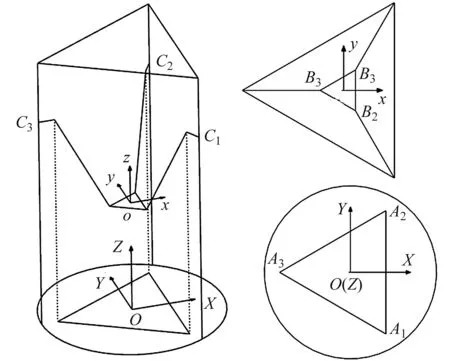
图2 机构位置结构简图
图2中,固定平台简化为等边三角形A1A2A3,其外接圆半径为R;动平台简化为等边三角形B1B2B3,其外接圆半径为r;在动平台上建立动坐标系,动坐标系原点位于动平台B1B2B3的中心,x轴垂直于B1B2,y轴平行于B1B2,z轴由右手坐标系得到;在固定平台上建立静坐标,原点O位于三角形A1A2A3的角平分线的交点,坐标轴的建立和动平台相同。
该并联机构的主要结构参数如表1所示。

表1 并联机构结构参数
本文研究的并联机构的材料为45#钢,动平台的质量ma=0.336 kg,滑块的质量为m1=0.167 kg,连杆的质量为m2=0.028 kg。
通过对该机构分析,得到该机构的Lagrange动力学模型[14-16],表示广义坐标x、y、z方向上广义力:
(1)
记为:
(2)
通过力的雅各比矩阵得出在驱动滑块所需的驱动力表达式为:
(3)
鉴于文章篇幅,此处不再详细列出其推导过程。
2 三平移Delta并联机构加速度分析
2.1 三平移Delta机构的二阶影响系数矩阵
根据三平移Delta并联机构的性质可知,当确定3个驱动滑块的输入位移d1、d2、d3,动平台的位姿可以由其质心坐标x、y、z唯一确定。
动平台的位姿可以表示为U={x,y,z}T,对应的3个驱动滑块的位置为d={d1,d2,d3}T,如图3所示。
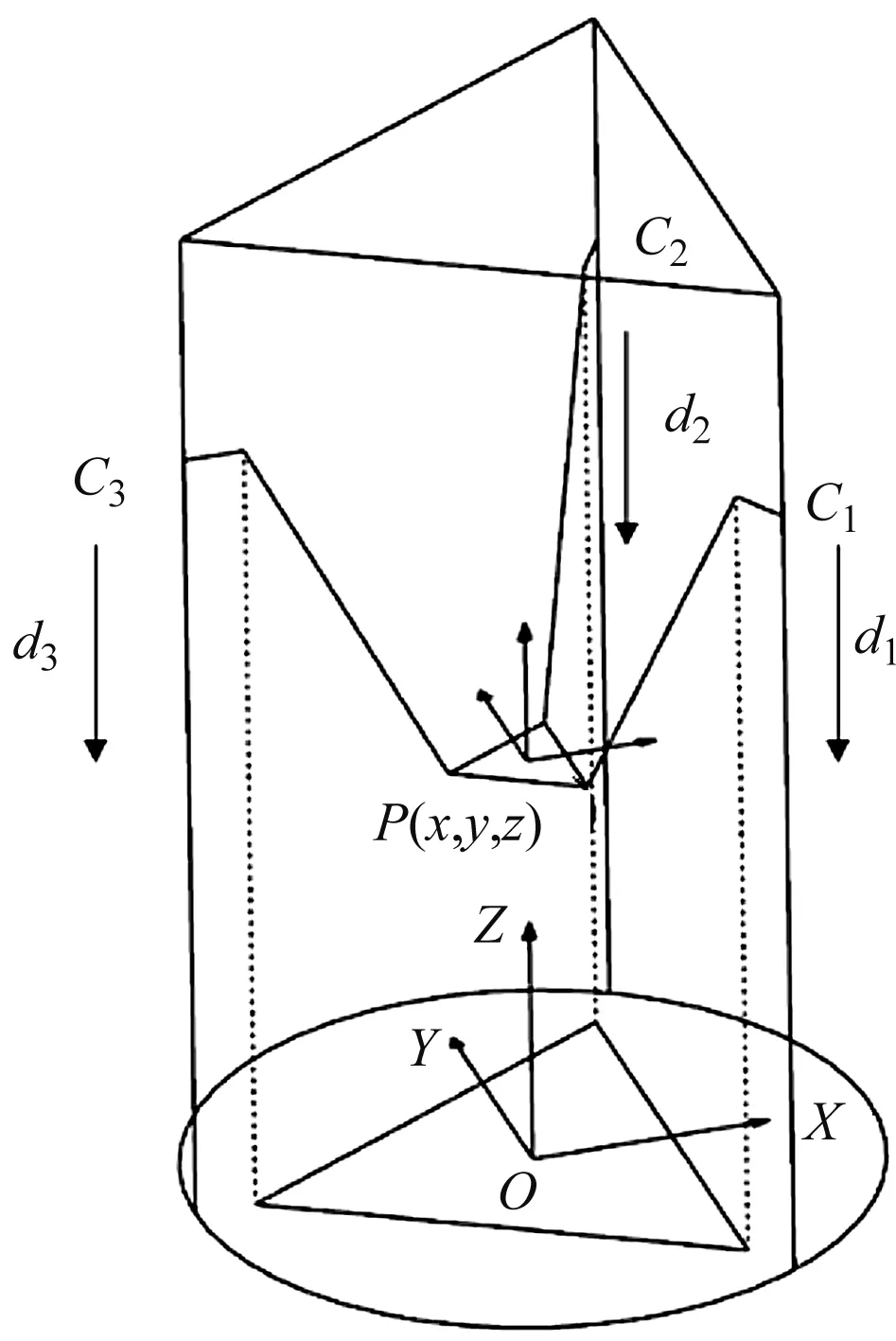
图3 三平移Delta并联机构简化图
根据图3可列出位移方程组:
(4)
输入位移d1、d2、d3和输出广义坐标x、y、z均随时间变化,将式(4)对时间进行隐函数求导,可以得到:
(5)
整理后可以得到其矩阵形式,即:
(6)

(7)
式中:矩阵[G]—该三平移Delta并联机构的一阶影响系数矩阵(Jacobian矩阵)[17]182-185。
式(7)再次对时间求导,经简化整理后可得:
(8)
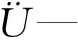
式(8)可以写成矩阵形式:
(9)
式中:[H]—该并联机构的二阶段影响矩阵(Hessian矩阵)[17]186-190。
从式(8,9)可得到二阶段影响矩阵的表达式为:
(10)
将二阶段影响矩阵展开,有:
(11)
由式(11)可以看出,二阶影响系数矩阵[H]是一个三维立体矩阵,即二阶影响系数矩阵中的每个元素均为一个3×1的列向量。每个元素表达式为[17]189-190:
(12)
2.2 三平移Delta并联机构加速度分析和计算
设执行机构的加速度表示为:a0={ax,ay,az}T,3个滑块的加速度为:ad={a1,a2,a3}T,根据式(9)可以求出驱动滑块加速度,即:
(13)
式中:v0—动平台的速度,v0={vx,vy,vz}T;[J]—一阶影响系数矩阵,式(7)中矩阵[G]的逆矩阵;[Hd]{d=1,2,3}—二阶影响系数矩阵。
[Hd]展开后的表达式为:
(14)
(15)
(16)
在该并联机构的动平台添加空间圆锥螺旋线的运动轨迹,其曲线方程为:
(17)
在该运动轨迹下,使用MATLAB求解三平移Delta机构3个驱动滑块的加速度,得到的加速度时间曲线如图4所示。
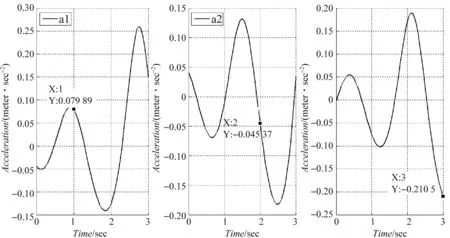
图4 三平移Delta机构加速度时间曲线(MATLAB)
图4中,从左向右依次为驱动滑块1、滑块2和滑块3的加速度时间曲线.
2.3 三平移Delta并联机构加速度仿真分析
在ADAMS中建立该并联机构的虚拟样机,如图5所示。
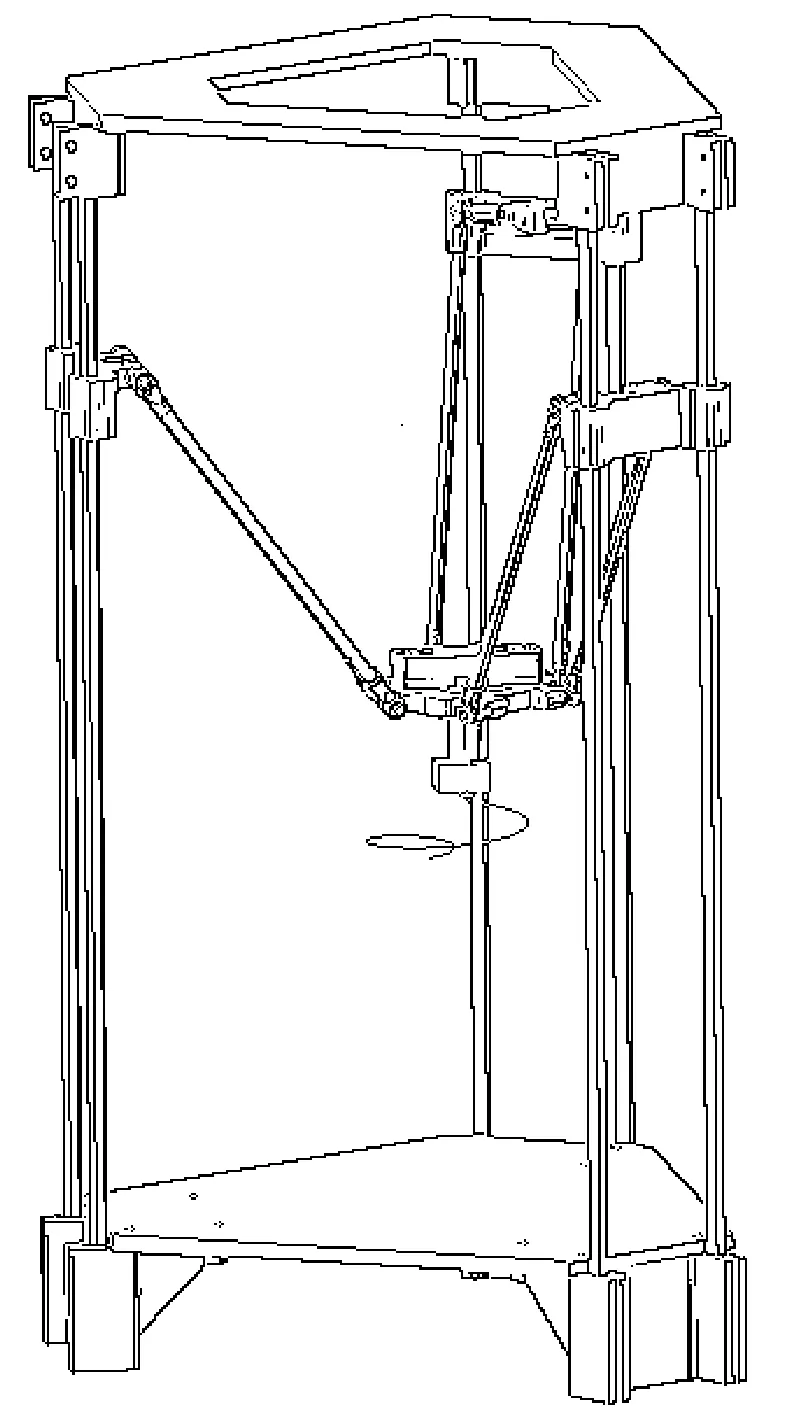
图5 三平移Delta机构加速度时间曲线
在并联机构虚拟样机的动平台上添加运动驱动,运动驱动轨迹方程如式(17)所示。图5为Delta并联机构的运动仿真,显示出动平台的运动轨迹为空间圆锥螺旋线[18-19]。
仿真完成后,可得3个驱动滑块的加速度时间曲线,如图6所示。
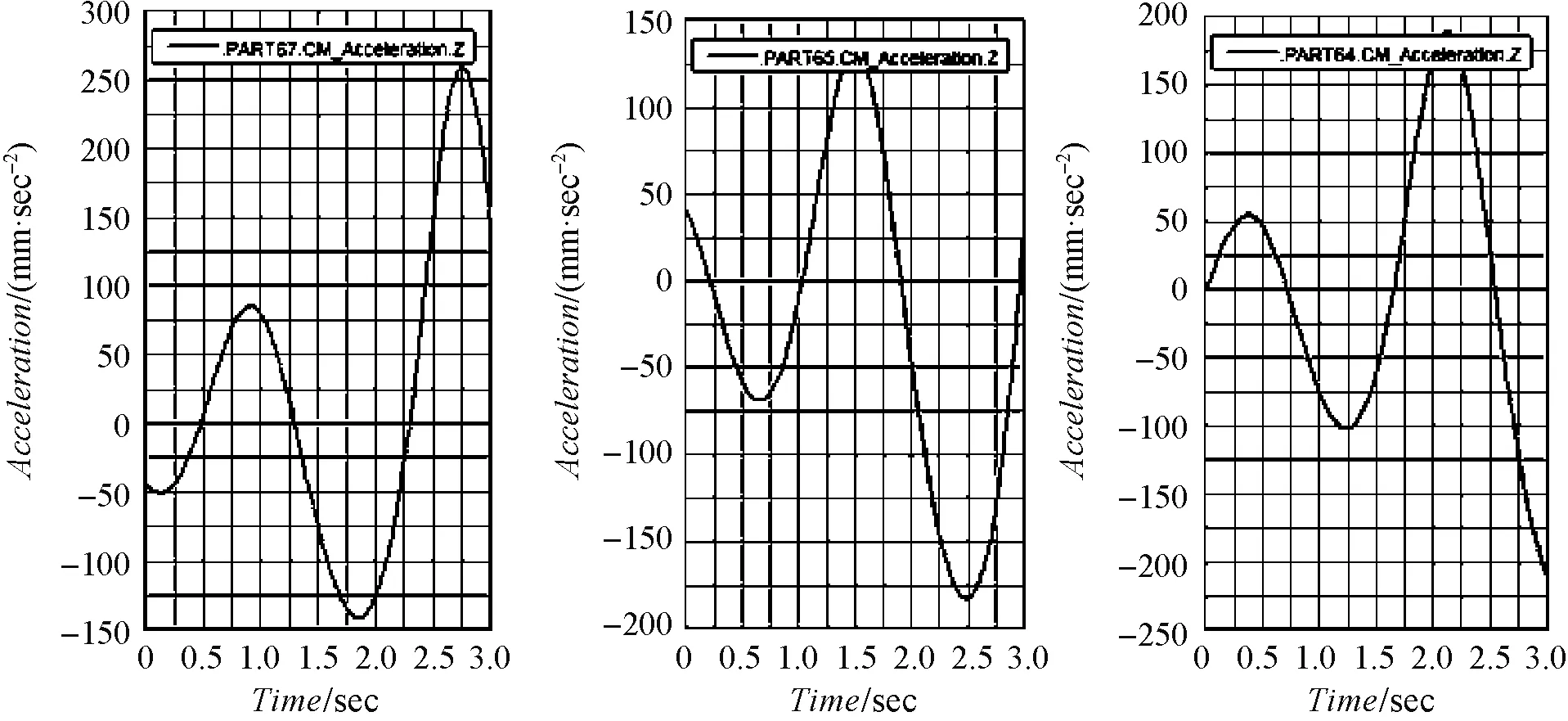
图6 三平移Delta机构加速度时间曲线(ADAMS)
图6中,从左至右依次为滑块1、滑块2、滑块3的加速度时间曲线。
在图4中,t=1 s时,滑块一的加速度a1=0.079 9 m/s2;t=2 s时,滑块二加速度a2=-0.045 m/s2;t=3 s时,滑块三的加速度为a3=0.21 m/s2。
而在图6中,即ADAMS的仿真结果中,t=1 s,滑块一的加速度a1=0.079 9 m/s2;t=2 s时,滑块二的加速度a2=0.045 m/s2;t=3 s时,滑块三的加速度a3=0.21 m/s2。可以看出,ADAMS仿真得到加速度的值与在MATLAB数值计算的结果吻合,验证了该加速度逆解数学模型的正确性,也证明了ADAMS仿真的正确性。
3 驱动滑块约束力分析
3.1 三平移Delta并联机构的约束力分析基础
为方便三平移Delta并联机构约束力的分析,需要做一些准备工作,具体如下:
(1)以驱动滑块1为例,设动平台中心坐标在静坐标系中表示为Om(xm,ym,zm),与驱动滑块1相连的连杆B1C1两端的坐标点分别用B1和C1表示:
(18)
(19)
可以得到连杆B1C1的向量为:
(20)
根据并联机构的运动学反解,在已知动平台位姿时,3个驱动滑块的Z方向位移可以表示为d1、d2和d3:
(21)
篇幅所限,这里不再给出其具体求解过程。
(2)该Delta并联机构的3个分支均为4S闭环,并且为平行四边形,如图7所示。
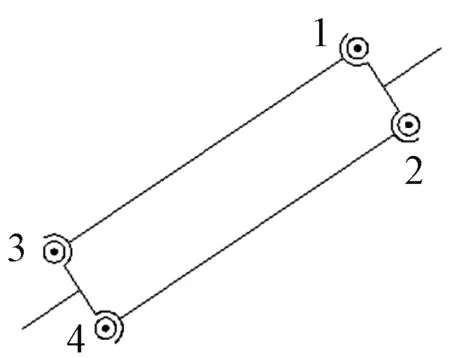
图7 Delta机构4S平行四边形闭环
球铰1、2处连接驱动滑块,球铰3、4处连接动平台,根据螺旋理论可以知道,球铰1、2处的约束力方向均是沿着分杆13和分杆24的轴向[20],本文将该并联机构进行简化。
在图7中,笔者将4S平行四边形机构简化成一个连杆,即球铰1和2合并,3和4合并。
驱动滑块受力分析图8所示。
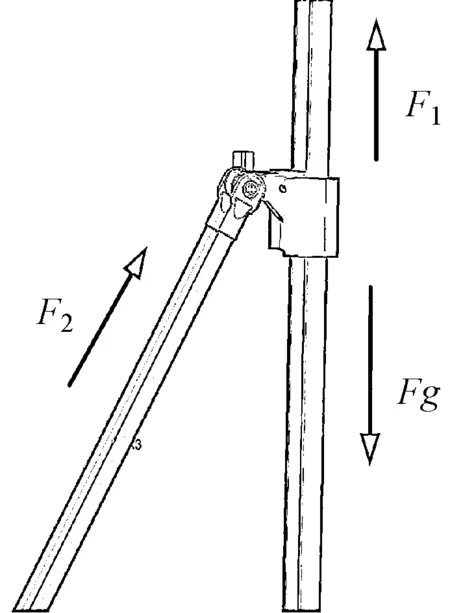
图8 驱动滑块受力分析图
(3)连杆B1C1约束力分析如图9所示。
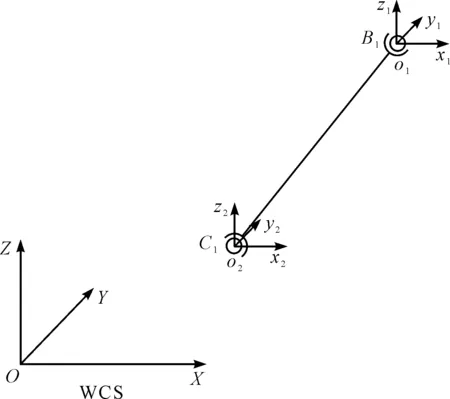
图9 连杆B1C1约束力分析
图9中,在连杆B1C1中,作用在滑块1中球铰的约束力方向沿向量连杆B1C1轴线方向。为了方便求解连杆两端球铰水平方向约束力,笔者在连杆B1C1两端球铰球心处添加两个局部坐标系Ol-xlylzl和Op-xpypzp,两个局部坐标系的X、Y、Z轴均和世界坐标系的X、Y、Z轴方向一致。
3.2 约束力竖直方向分力求解及仿真
根据前面的分析,可以得到驱动滑块竖直方向受力情况,如图10所示。
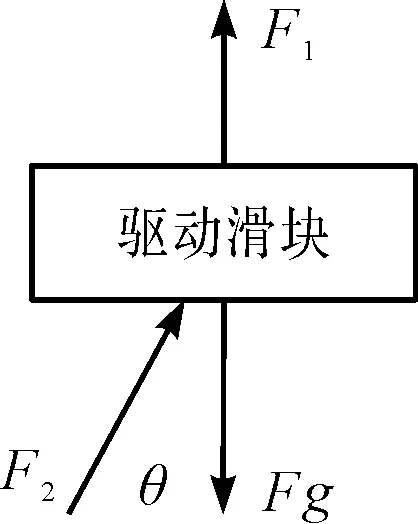
图10 驱动滑块受力分析图
该并联机构的材质为铁,滑块1上的驱动力为F1,加速度为ad1,球铰处对驱动滑块在竖直方向的约束力分力用F21表示。根据图10,在忽略摩擦力的前体下,滑块1竖直方向的受力为:
F1+Fg+F21=ma
(22)
笔者在MATLAB对式(22)进行求解,得到球铰竖直方向的分力如图11所示。
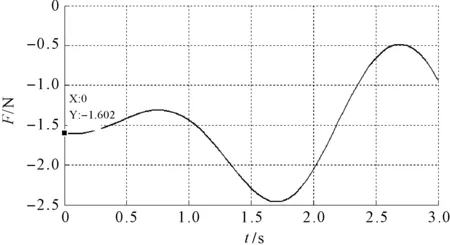
图11 MATLAB中驱动滑块1处球铰约束竖直方向分力
笔者在ADAMS中对该并联机构进行动力学仿真,给3个驱动滑块添加驱动,动平台运动轨迹如式(17)。
对驱动滑块处球铰约束力竖直分力进行求解,得到球铰的约束力竖直方向受力如图12所示。

图12 ADAMS中驱动滑块1处约束力的竖直方向分力
从图11、图12可以看出:两者的结果吻合,验证了Lagrange方程和二阶影响系数矩阵对球铰连接处竖直方向约束力分析结果的正确性。
3.3 约束力水平方向分力分析
对约束力水平方向分力的分析将会涉及到连杆,需要建立连杆的质心连体坐标系ol-xlylzl和质心平动坐标系op-xpypzp,对连杆的转动惯量进行坐标间变换,这里研究对象为连杆B1C1。
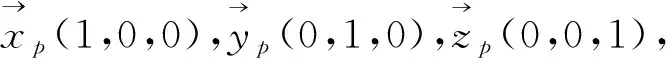
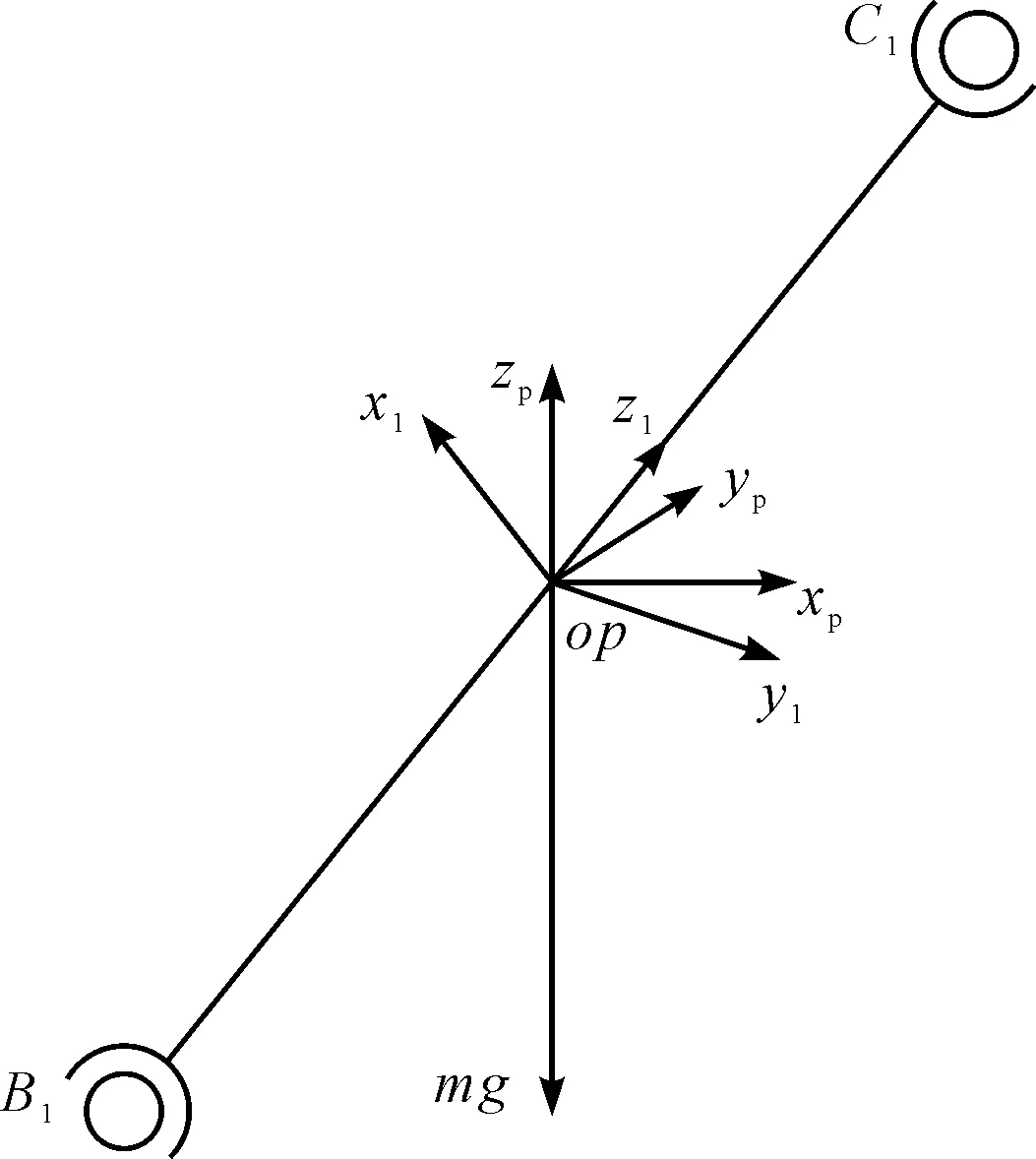
图13 连杆的连体坐标系和质心平动坐标系
质心连体坐标系的原点仍定义在连杆B1C1质心处,质心连体坐标系的Z轴正向单位向量定义如式(23)所示,根据该并联机构的结构尺寸,得到其表达式为式(24),为了便于表达,Z轴正向单位向量在静坐标系各轴分量用zl1、zl2、zl3表示,即:
(23)
(24)
坐标系ol-xlylzl的其他坐标轴的正向单位向量定义表达式为:
(25)
(26)
根据式(24~26),可以确定出质心连体坐标系o1-x1y1z1相对于质心平动坐标系的方向余弦矩阵为:
(27)
根据刚体的惯量张量在连心坐标系间的变换公式[21],已知连杆B1C1在质心连体坐标系下的惯性张量Il和连体坐标系相对于质心平动坐标系的方向余弦矩阵Cpl,可以求出连杆B1C1在质心平动坐标系的惯性张量Ip。连体坐标系O1-x1y1z1为连杆的惯性主轴坐标系,可知连杆在质心平动坐标系中的转动惯性张量Ip,即:
Ip=[Cpi]*Il*[Cpi]T
(28)
经分解后得到的连杆所受约束力如图14所示。

图14 连杆的所受约束力分解
根据上述分析以及刚体一般运动微分方程(8),可以写出连杆沿质心平动坐标系的xp轴方向的受力平衡方程和绕yp轴的力矩平衡方程,即:
(29)
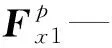

(30)
通过MATLAB对式(29)进行解算,并在ADAMS中获取对应球铰的水平方向X轴约束力。
MATLAB中球铰C1的X方向分力如图15所示。

图15 MATLAB中计算得出球铰C1的X方向分力
ADAMS中球铰C1的X方向分力如图16所示。

图16 ADAMS中计算得出球铰C1的X方向分力
在该并联机构的ADAMS仿真模型中,一个分支有4个球铰,而文中的数学计算模型对分支球铰进行了合并,故ADAMS仿真对一个分支中同一端的两个球铰在X方向的约束分力进行求和。
由图(15,16)可看出:在MATLAB和ADAMS中,计算得到的球铰约束力的X方向分力比较接近,存在的细微偏差是由于合理假设导致的,该结果验证了本文对约束力分析的正确性。
球铰约束力的Y、X方向分量分析过程类似,此处不再重复。
4 实验验证
为了验证本文的结论,笔者使用现有的三平移Delta并联机构运动平台进行实验,如图17所示。

图17 三平移Delta并联机构
图17中,该并联机构的控制单元采用Arduino板,对执行机构进行轨迹规划,使其运动轨迹如图5中的螺旋线。
笔者使用MPU-6050加速度计采集驱动滑块1的竖直方向的加速度数据,并使用均值滤波得到较平滑的数据;在MATLAB中打开该加速度文件,并绘制折线图,如图18所示。

图18 MPU-6050加速度计采集的滑块1的加速度数据
笔者根据式(22)和滑块1的竖直方向加速度数据得到其竖直方向的合外力,如图19所示。

图19 实验所得的滑块1所受合外力
从图19中可以看到:驱动滑块1的合外力和图11中通过公式计算所得的合外力数据趋势吻合;其最大值、最小值也比较接近。该结果验证了本文结论的正确性。
5 结束语
本研究使用Lagrange方程和二阶影响系数矩阵,建立了三平移Delta并联机构驱动滑块球铰处的约束力方程,运用MATLAB对约束力方程进行了求解,并用ADAMS方程对约束力方程进行了验证;最后,通过实验数据对仿真结果进行了验证。
研究结果表明:
(1)使用Lagrange方程和二阶影响系数矩阵建立的约束力方程,其表达式规范、简洁,方程数量减少约1/2;
(2)将二阶影响系数矩阵和Lagrange方程结合,分析并联机构的约束力,简化了约束力的推导过程,得到的约束力分析结果准确,有一定程度的方法创新。
下一阶段,笔者将会把本研究成果推广应用到其他构型的并联机构,以提升该约束力算法的通用性、稳定性和运算速度;并且,笔者还将致力于开发具有自主知识产权的并联机构专用三维动力学分析软件系统。
