几何直观能力发展“四步”

方芳

[摘 要]几何直观就是运用图形的直观性来作为解决抽象问题的有力武器。几何直观能力包括空间想象力、数形转化能力、读图能力和画图能力，对这些能力的培养需要经过“孕育→过渡→发育→爆发”这四步。

[关键词]几何直观能力;孕育;过渡;发育;爆发

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2021）35-0067-02

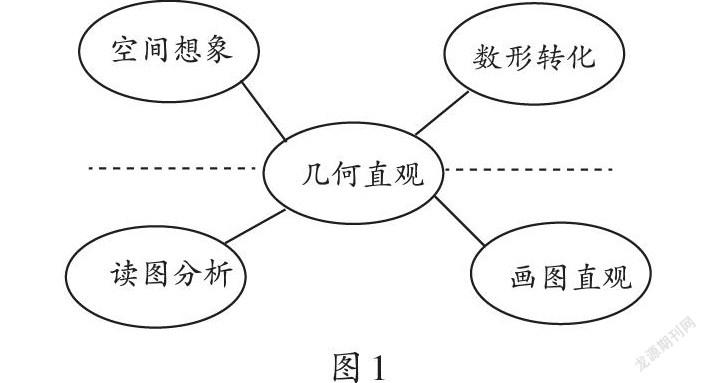
“几何”既可以作为研究对象，也可以作为一种研究工具，几何直观就是运用图形的直观性来作为解决抽象问题的有力武器，它本质上和实物直观相同，但是又要比实物直观抽象一些，它会将数学信息符号化。需要注意的是，运用几何直观并不是只能研究几何问题，许多复杂难解的代数问题也可以通过几何直观反映得清清楚楚，清晰明了。基于以上认识，笔者将“几何直观”能力进行科学分层，具体如图1所示。

几何直观就是将几何图形作为研究问题的思想工具，既然是工具，学生就要对它的构造、功能、用法、操作程序非常熟悉。作为一种靠线条组装起来的特殊工具，“用户”的空间想象能力就成了必备技能。此外，数形转换能力是几何直观能力的基本功，即需将代数问题转换成图形语言，不仅如此，在具体操作时，代数语言和图形语言是要交互循环印证的，所以，需要学生具备双向互译的能力。

读图能力和画图能力是几何直观能力的两大支柱。前者指的是借助图形语言来理解原问题，后者则是将自己对原问题的分析思路与解答过程用几何图形记录下来。几何直观能力含义丰富、结构宏大，因此，学生几何直观能力的培养与形成必须循序渐进、步步为营。笔者简略将其分为四步：孕育→过渡→发育→爆发，每一步都各有偏重。本文尝试结合教学实践来一一解说这四步的“基本步法”。

一、孕育阶段——直观学具的初步抽象化处理

小学生的几何直观能力主要在一、二年级孕育发展。这个年龄段的学生以动作思维、形象思维为主，因此，数学教学大量采用直观法。但此时的直观教学主要还停留在学具、图片、符号等稚拙载体的使用阶段，离简明精巧的几何直观还有一段距离。因而适度进行抽象，由实物、符号直观慢慢向图形直观靠拢转型，非常有必要。

例如，教学人教版教材第二册中的“100以内数的认识”时，教材运用曲别针、小棒、小木块等实物来演示数的组成，揭示计数单位。这是通过实物来达到直观认识数的目的，因而可以归为实物直观。从几何直观的视域来看，这三种学具中哪一种更具向几何直观转型的可塑性？先看曲别针，“10个曲别针一小堆”“100个曲别针一大堆”分别代表着计数单位“十”和“百”;再看小棒，则是“10根一小捆”“100根一大捆”;最后看小木块，1个小木块代表计数单位“一”，10个小木块一字排开，代表计数单位“十”，再将这样的10排纵向摆开，代表计数单位“百”。如果仅局限于这一课时的教学目标，三者相差无几，但是如果从后续培养学生几何直观的战略部署来考量，显然小木块更符合要求。因为小木块的组接方式生动形象地展现了“点—线—面”的几何图形特征，可以说，在某种程度上小木块具备了几何直观的抽象性，并为进一步认识计数单位“千”（体）埋下伏笔（如图2）。这样具有关联性和延续性的组接方式，为计数单位与几何模型搭建了沟通的桥梁，从而促进学生几何直观能力的发展。

二、过渡阶段——注重几何操作经验的积累

“几何直观”需要不断地进行直观操作或直观认读，积累直观表象反复刺激带来的固定思维。数学基本活动经验分为操作经验和思维经验，两者必须通过长期重复的数学活动才能获得。

小学阶段的图形学习，要么采用直观几何的方式，要么采用实验几何的方式，前者通过观察、测量了解图形的特征，后者通过触摸、翻转、拆卸、拼装等途径来了解立体图形的特征。其中，平面图形（如线段、直线、射线、角、多边形等）的认识主要集中在三、四年级，这正是几何直观能力发展的过渡阶段。教学中，一方面要坚持“观察、拼搭、折叠、勾画”等手工操作，帮助学生积累实践经验;另一方面，要强调描画联想和描述解说，一步步将学生的实践经验转为思维经验。

下面，以“三角形的内角和”的教学为例：

通常来讲，探究三角形内角和有三大方法：（1）先用刻度尺直接测量三个内角的大小，再求和;（2）切割同一个三角形的三个内角，重组成一个平角;（3）通过翻折，将同一个三角形的三个内角拼凑成一个平角。

显然，这三种研究方法都属于实践操作类型，其说服力不如几何论证，因为操作本身存在误差，而且还会受到材质的影响。但笔者还是支持动手实践，因为结果是否有误差不重要，结论是否顺利得出也不重要，重在过程，重在学生从实践活动中积累的活动经验以及感性认知。沿着这个教学方针，可以综合三种方法的优势，采用几何作图的方法（如图3），设法将三个内角拼装起来，体现“求和”的思想。这样，实践经验就成功转变为思维经验，为初中的几何证明打下基础。

三、发育阶段——关注几何直观意识的培养

通常，进入小学四年级，学生的几何直观能力开始发育。这是因为一方面学生的几何知识日趋丰富，另一方面，数学知识的抽象性与日俱增，理解起来愈加依赖直观形象的佐证。为了顺应学生思维能力的发展趋势，此时直观材料由实物变为图形，在这个阶段，教师要有意识地渗透几何直观的运用意识，也就是要诱导和督促学生用几何直观分析问题，让学生看到几何直观的巨大价值和运用前景。

如学习“异分母分数加、减法”时，对于算式[12]+[25]，学生一般会出现以下几种算法：（1）[12]+[25]=[37];（2）[12]+[25]= [510]+[410]=[910];（3）[12]+[25]=0.5+0.4=0.9。在这里，理解通分的必要性是难点，它与整数加减法中的“相同计数单位累加”一脉相承，如果要用几何直观解释的话，“分数墙”（如图4）是再好不過的。从图4中能直观看出，由于每一个“分数条”的长短和面积不同，无法直接纵向合并成一个新的分数条，每个分数条代表一个计数单位，所以不同分数单位不能直接相加减。

进一步指示学生在“墙壁”上搜寻与[12]和[25]等值的分数，发现1个[12]等同于5个[110]，2个[15]等同于4 个[110]，由于兑换成的新分数条的大小相同，所以可以直接累计分数条的个数，而转化为小数再计算，与通分是一个道理。

四、爆发阶段——关注数形之间的转换训练

五、六年级学生的几何直观能力进入爆发期。此时学生需要具备强大的数形转换能力。数形转换，也就是数与形互通互译。教学中，一方面适当地加大图形化的力度，如频繁进行“看图写数（式）”“看数（式）画图”的操作等;另一方面，通过操作活动实现数形互换互转。如“正方形数”的认识，先呈现图5，指引学生观察并思索：以下点阵图各自代表什么数字？点阵图的排列有何规律？通过讨论交流，明确这样的数称为“正方形数”。再通过进一步的图形推演（分点或连点）自主创建“正方形数”的不同形式的数学模型，如构建完全平方数 n²;表示为从1开始的连续奇数之和：1+3+5+…+ n;构建“回”字形结构：4+3+3+2+2+1+1;设计为两个“三角形数”之和：1+2+3+…+ n +…+3+2+1。（如图6）

像“三角形数”“正方形数”等都是带有明显几何特性的数，巧用这样的素材来勾连数形之间的关系，反复在数与形之间来回切换，对发展学生的几何想象力、揭示数形之间的亲密关系意义重大。

值得警惕的是，就整体而言，小学生的几何直观能力是强弱不均的;就个体而言，其发展也是曲折回旋的。因此，本文提到的“四步”只是一个大概的划分，没有具体的分隔线，但是其发展变化的规律还是明确的，不同阶段培养的策略各有偏重。事实上，受到学生年龄和学科内容的限制，小学生的几何直观能力尚处初级阶段，但基本几何知识的掌握、活动经验的汲取、几何直观意识的形成必定能为学生未来的发展打好根基。

（责编 罗 艳）