基于思维可视化的教学策略

刘品兰 谭敏

[摘 要]很多学生在小学和初中阶段学习优秀，但是到了高中阶段就会在学习上感到困难，尤其是物理学科，这大都是因为思维方法上存在问题。理科思维应从小学阶段开始培养，小学数学和高中物理在思维方法上是共通的，在小学数学教学中，教师培养学生的理科思维，可让学生对后学段学习进行灵活迁移和应用。

[关键词]小学数学;高中物理;思维可视化;理科思维

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2021）35-0046-02

一、理论基础

1.沉锚效应

沉锚效应，指的是人们在作决策和判断时易受第一印象或第一信息支配，就像沉入海底的锚一样把人们的思想固定在某处。按照这个理论，学生最早养成的思维习惯将会成为以后解决问题时最先依赖的思考方式。因此，在小学阶段，教师就要让学生勤于思考、重视过程与方法、形成良好的思维习惯，掌握对后学段学习有利的思维方式，为后学段的学习奠定良好的基础。

2.迁移理论

在学习过程中，学生是信息加工的主体，是意义的主动建构者，而不是知识的被动接受者。在学习中，除了具体的知识，学生也会把以前掌握的思维方法，自觉地迁移应用到新知的学习中，从而构建自己的认知体系，并且这个迁移是没有学科界限的。思维方法处于知识的上位，其掌握的程度决定着学生大脑中概念的抽象性、概括性和包容性水平。这些水平越高，学生举一反三的能力就越强，思维越深刻，智慧水平越高。对此，小学阶段就要让学生在学习过程中掌握知识蕴含的思维方法，这能够让其在后学段的理科学习中提高学习效率。

二、小学数学思维与高中物理思维的联系

学科的思维方法不是具体的学科知识，而是基于具体的学科概念、原理和定律。通过探讨学科的内在特点和规律，整理和总结出来的思想观念、思维方式和学习方法，能体现该学科的本质与价值，为学生提供了一种独立学习、探究的方法，有助于提高学生问题解决能力和学科创新能力。

由于思維方法具有跨学科性，小学阶段学到的数学思维方法也常被应用于物理学科的学习中。例如，小学画图解题的数形结合思维经常用来处理高中物理的运动图像问题;小学数学解应用题中学到的程序思维用于处理多过程的物理问题;小学阶段推导圆面积所用的逼近思想用于高中推导匀变速直线运动的位移和时间关系公式;小学数学中的等效替换的解题技巧常用于物理电路学问题中的等效电阻、等效电源等。

三、学生物理思维的现状及应对策略

1.现状

小学生的思维方式以感性思维为主，尤其在低年级，很多时候学生仅仅靠对知识的表层理解和记忆，就能在考试中取得不错的成绩。如果长时间使用这种功利化的教学方式，学生就容易养成懒于思考的不良习惯，错过掌握相应思维方法的最好时机。当面对高中物理问题时，不会将对应的思维方法合理迁移到学习中，也无法将物理思维同化到已有的认识模式中。

2.应对策略

思维可视化就是指以图示的方式把原本不可见的思维结构、思考路径及方法变得可见的过程。它可以给以感性认识为主的小学生更加直观和形象的理解。思考赋予了知识生命力，离开思考的学习必然是枯燥而低效的，提高教学效能的关键在于挖掘与呈现知识背后的思维规律并让学生掌握它。因此，在平时的教学中，教师要让学生主动思考和探究，利用思维可视化的策略，让学生活动过程中的思维从不可见变得可见，提高学习效率。

四、教学案例

1.守恒的思维

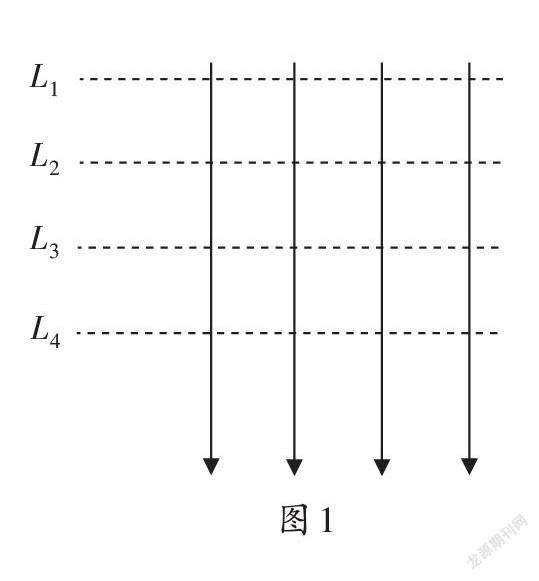
【例1】如图1所示的匀强电场中，虚线为等差等势面。一个正电荷在等势面L3处的动能为20 J，运动到等势面L1处时动能为零。现取L2为零电势参考平面，则当此电荷的电势能为4 J时，它的动能是多少？（不计重力及空气阻力）

这是高二物理静电场中的一个常见问题，对初学者来说较难。该题目情景中仅有电场力做功，所以电荷的电势能和动能此消彼长，总能量是守恒的，解决问题的关键就在于找出这个总能量。在小学数学学习中，也有很多类似的题目，教师可以在平时的教学中有意强化这种思维。

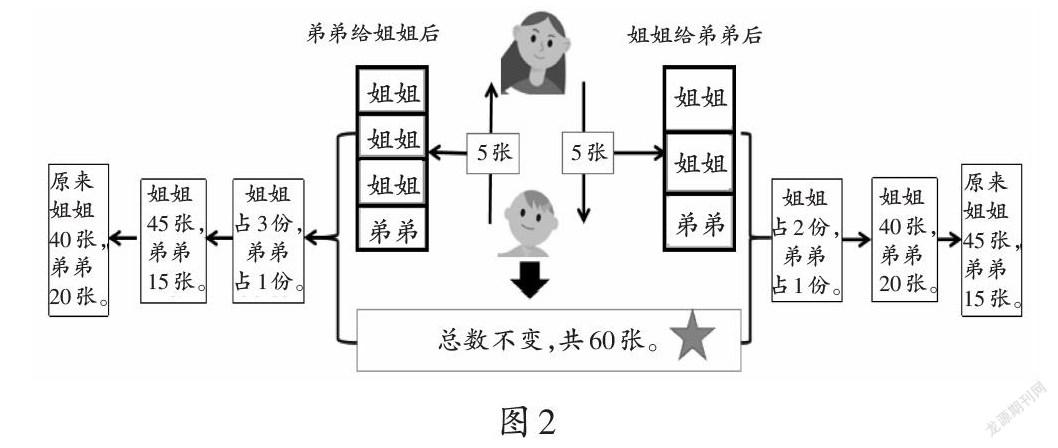
【例2】姐姐和弟弟共有60张邮票。（1）如果姐姐给弟弟5张后，姐姐的邮票数量是弟弟的2倍，姐姐和弟弟原来各有多少张邮票？（2）如果弟弟给姐姐5张后，姐姐的邮票数量是弟弟的3倍，姐姐和弟弟原来各有多少张邮票？

通过图示（如图2），首先明确无论姐弟之间怎么互给邮票，总数都是不变的。然后，引导学生找到最终姐弟各自的邮票在总份数中所占的份数，从而求出现在各自的数量，再推导出原来的数量。最后，再对这类题型进行总结，让学生明白在解决问题中抓住守恒思维的重要性，理解在变化之中有不变，不变的量往往就是解决问题的突破口。

2.转换的思维

【例3】如图3所示，一条形磁铁静止在斜面上，固定在磁铁中心的竖直上方的水平导线中通有垂直纸面向里的恒定电流，如果增大导线中的电流，试分析磁铁对斜面的压力F和摩擦力f的变化情况。

这是高中物理中常见的题型，如果选用常规的思维直接研究磁铁将很难入手，解题的关键是利用牛顿第三定律转而思考导线的受力情况，通过转换研究对象来解决问题。为了让学生掌握这种思维方法，笔者在教学中选取了下面的题目。

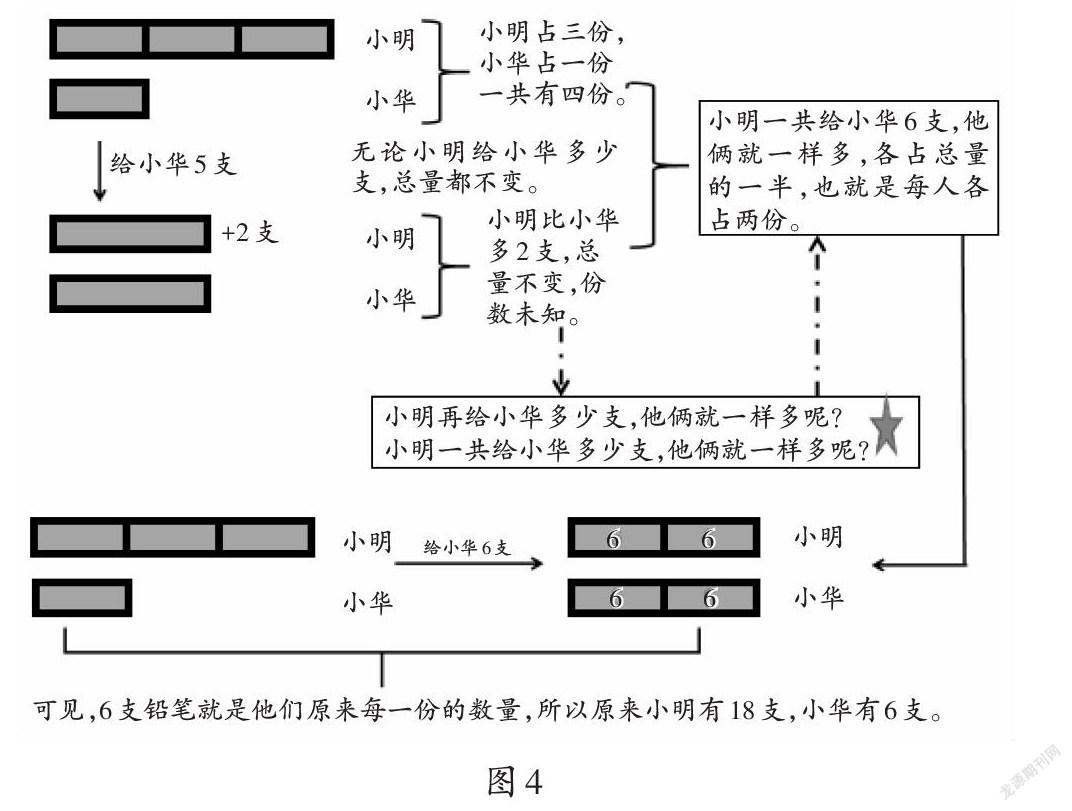
【例4】小明的铅笔支数是小华的3倍，如果小明给小华5支，小明比小华还多2支。两人原来各有铅笔多少支？

如图4所示的思维过程中，无论这两人之间怎么互给铅笔，铅笔总数不变。在给铅笔之前，两人的铅笔数量之间有倍数关系，如果在给了铅笔后仍然有倍数关系，那么这个问题就会变得容易一些，但是给了5支铅笔后，他们之间的倍数关系不明确了。因此，可以将问题转化为怎么给铅笔能够找到新的倍数关系。通过引导，学生发现当小明给小华6支铅笔后，他们就一样多了，再利用关系图对比，就知道两人各自原来的铅笔数量。通过图示对思维的具体表现，学生学会了将问题进行转化来解决。

思维方法比具体的学科知识更重要，当学生学会把各个学科的思维方法加以综合运用并跨学科迁移，其学习的效率和应用新知的能力也会得到提升。小学数学中蕴含着许多对高中物理乃至终身学习非常重要的思维方法，这就需要我们在小学阶段有意识地强化学生对这些思维方法的掌握，全面提升学生的思维能力，为后面的学习做好准备。

[ 参 考 文 献 ]

[1] 李维娜.“沉锚效应”下的教学及其反思[J].中小学数学：小学版，2019（10）.

[2] 张承芬.教育心理学[M].济南：山东教育出版社，2010.

[3] 马立丽，金洪源.提高学科学习能力的元认知策略与培养[M].沈阳：辽宁科学技术出版社，2016.

[4] 陈涵.浅谈跨学科思想方法在高中物理教学中的融入[J].湖南中学物理，2020，35（08）.

[5] 陈涵.利用“思维可视化”培养高一学生物理解题思维[J].湖南中学物理，2017，32（06）.

（责编 李琪琦）