解题教学需要教会学生思考

张莉莉 陈玲玲

[摘  要] 思考不仅是一种思维方式，还是一种数学能力的表现，数学解题能力的培养应该基于学生已有的认知结构进行思考，因此努力将学生培养成一名“思考者”对解题能力的提升具有十分重要的意义. 文章结合例题，从教会学生理解题意、教会学生找寻思路、教会学生怎样思考这三个方面，探究如何促进学生主动思考，学会思考，提升学生的解题能力.

[关键词] 解题教学;理解题意;找寻思路;怎样思考

涂荣豹先生曾说：“每节课都需把学生认知能力的发展作为教学的最大目標. ” 认知能力是一种基本能力，包括观察能力、记忆能力、想象能力、创造能力、思维能力等，其中的思维能力是占据核心地位的一种. 而大部分地区的数学教学，由于受到以应试为导向、解题训练为重心的教学模式的束缚，使得大部分学生在数学学习过程中，过度依赖教师，很少探究、缺乏思考、不会学习. 因此，当前教师最重要的认识是需要在“教会学生思考”上下一番功夫. 本文从解题教学的视角着手，谈谈如何促进学生主动思考，并努力将学生培养成一名“思考者”.

给予搭桥引路，教会学生理解题意

教育心理学实践表明：那些学生想不到的、理解不了的解题，是低效的. 如何让学生主动思考题目的内涵，从而达到理解题意的目的，是实现正确解题的第一步. 事实上，由教师来选择具有典型性的例题，设计“自然”的理解思路来搭桥引路，让学生学习理解题意，无疑是一条有效的途径. 而在逐步理解和寻求思路的过程中，就是为“所有”和“所无”搭建桥梁的过程，一些简单题型只需搭建一座桥梁即可变“所无”为“所有”，而一些难题则需要经历多搭建几座桥梁方能达到成功的彼岸.

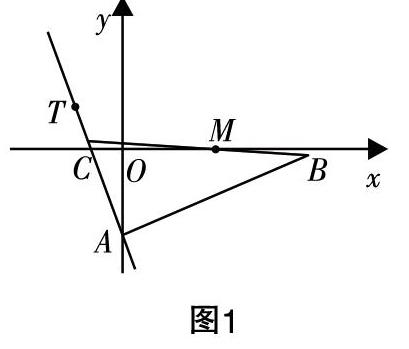
例1：如图1，已知Rt△ABC中，∠A=90°，且边AB所在的直线方程是x-3y-6=0，点T（-1，1）位于直线AC上，M（2，0）为BC中点，试求出边BC所在的直线方程.

以上问题的理解，除去鼓励学生多读几遍题目，并将条件以数学符号的形式在图形中认真标注，以达到“关注每一个条件”的目的之外，还须有意识地进行一连串的追问：①求什么？（边BC所在的直线方程）②条件中提供了什么？（点M的坐标）③那还需要什么？（需要提供一个条件）④现在我们有什么条件？（∠A=90°，且边AB所在的直线方程是x-3y-6=0，点T（-1，1）位于直线AC上）⑤由这些条件可得到什么？（直线AC）⑥那对所求问题有何用呢？（可求得点C的坐标）⑦还有什么条件是没有用到的呢？（斜边中点M（2，0））⑧可以怎么去用呢？（中点坐标公式）⑨可得到什么？（点B坐标）. 至此直线方程跃然眼前.

上例中，教师从解题思路的需要，搭桥引路出示了一连串自然的追问，是为了教会学生如何一步步正确理解题意，从而逐步走向问题本身，完善解题路径. 当然，这里若直接告知，学生也可以接受，但不利于其进行主动思考，易助长其依赖的心理. 因此，教师以此例为指导，让学生通过梳理与探究，获得解决问题的思路，从而明确解决问题的路径. 今后，遇到数学问题，学生自然有“法”可依，这样去教会学生理解题意，真可谓别出心裁，旨在教学生如何深入题目深处进行理解，学会主动思考，以达到正确解题的目的.

经历简单推理，教会学生找寻思路

不少学生在解决问题的过程中频频受挫，主要原因就是“找寻不到突破口”，即没有思路. 如何找寻到解决问题的思路呢？那么，在落实“理解题意”这一环节后，需着手构思找寻解题思路. 当然，这个思路可以是在解题的过程中逐步形成的，也可以是在历经多次探究失败之后瞬间闪现的“妙招”，而实现这一切的前提是我们需朝着“找寻思路”的目标跨出第一步.

例2：设1=a■≤a■≤…≤a■，其中a■，a■，a■，a■是公比为q的等比数列，而a■，a■，a■是公差为1的等差数列，则q的最小值是______.

找寻思路：①本题是一个什么问题？需要求什么？（本题为数列问题，且奇数项成等比数列，偶数项成等差数列，需要求q的最小值）②1=a■≤a■≤…≤a■代表什么？（代表的是a■=1的递增数列）③a■，a■，a■，a■成等比数列，这里的公比q还可以如何表示？（a■=a■q=1，a■=q2，a■=q3）④a■，a■，a■成等差数列，这里的公差为1还可以如何表示？（a■，a■=a■+1，a■=a■+2）⑤1=a■≤a■≤…≤a■还可以如何表示？（1≤a■≤q≤a■+1≤q2≤a■+2≤q3）⑥还缺什么？（a■与q）⑦那它们有何性质？（1≤a■≤q）⑧要求的是什么呢？（要使q最小，则只需a■最小，将a■=1代入1≤a■≤q≤a■+1≤q2≤a■+2≤q3，则有1≤q≤2≤q2≤3≤q3，再解以上不等式组求其交集，可得q≥■）

“逻辑推理”是数学的核心素养之一，就是从一些命题着手，从逻辑规则推导出一个命题的思维过程. 而初中数学中代数运算的要求并不高，导致了不少高中生的代数运算能力薄弱，最终在高考中面对一些代数推理的试题，不少学生都无从下手. 因此，高中时期教师需从简单的推理着手，强化代数推理的训练. 上例中，教师通过“范围”性质的例题，让学生进行推理，有意强化代数推理的训练. 学生在解题过程中，以向自己提问的方式找寻解题的思路，以小步伐的行走姿态逐步触及问题的底部，有效化解问题的难点，掌握解决问题的思路.

经历深入探究，教会学生怎样思考

新课程提倡：让学生以勇于探索的学习方式去体验数学发现的创造历程. 而在平时的解题教学中，笔者常常会遇到这样的现象：教师讲解的时候学生连连点头，感觉什么都懂，而待到做练习的时候就好似雾里看花而无处下手. 这是为什么呢？事实上，学生的困境不仅仅是接受能力差而导致的不善解题，原因当然众多，其中最突出的就是解题教学中教师仅仅是向学生展示“我是这样做的”，而没有将“我是这样做的”方法教给学生. 那如何才能真正教给学生呢？首先，自然是要找到“我是这样做的”的原因是什么？我是如何想到的呢？接着，就需想方设法让学生也想到，从而也这样去做. 因此，将自己的思考过程展现给学生，并引领学生经历深入探究，教会学生怎样思考，使学生知道怎样去思考，从而增强学生数学解题能力是十分必要的.

例3：若3a=0.618，a∈[k，k+1]，k∈Z，试求出k的值.

具体思考过程如下：①这是什么问题？要求的是什么？（这是一个求值问题，要求的是k的值，区间左端点）②条件中的3a=0.618是什么？（幂，那么当a为何值时3a=0.618？）③[k，k+1]又是什么？（k∈Z，[k，k+1]是相邻的整数区间）④a∈[k，k+1]又是什么？（k≤a≤k+1，此条件可以推出什么？）

就这样，教师预设一道例题，充分剖析自身的思考过程，让学生同自己一起经历问题解决的过程，教会学生怎样去思考问题解决的策略. 最后，在小结环节，教师让学生谈一谈自己有何收获，旨在教会学生知道怎样去思考一道试题，并留下深刻而清晰的印象.

写在最后

如何提升学生的解题能力？答案自然是丰富多彩的，不过要找到一件具有长效收益的事情，并从中获得成功的幸福感——那就是教会学生思考. 有了自主思考的能力，学生的解题能力就会逐步提高，他们的思维就会放宽，他们的解题策略就会变得无比丰富.

通过深入挖掘习题内涵，精心选择典型例题，通过搭桥引路，引发学生思考，教会学生理解题意，引领学生经历简单推理，教会学生找寻思路，使其经历深入探究，教会学生怎样思考，从而让学生学会解题，学会学习，会学数学，这是着眼于学生的长效发展，并服务于数学教育的最大目标. 当然，前景是美好的，但学生解题能力的培养也不是一蹴而就的，这是一个长期而曲折的过程，需要数学教师不断砥砺前行，由此为学生的发展谋一个好的前景.