题海无边,方法为船
2016-04-14张裕刚
张裕刚
摘 要: 学习数学离不开解题教学,反思解题所用到的知识和方法,以及和其他知识的联系等对提高解题能力非常重要,通过一题多解和多题一解对学生的思维能力进行训练和拓展,是数学解题教学的重要方法.
关键词: 解题教学 一题多解 多题一解
学好数学的重要途径是解题,题海战术固然不对,但离开解题要想学好数学也是万万不能的.著名数学家波利亚在《怎样解题》中将数学解题过程划分为四个阶段:弄清问题—拟定计划—实现计划—回顾,这个解题过程中的回顾就是解题反思.解题反思是对整个解题活动的反思,包含内容很广,如作者的命题意图是什么,这道题涉及那些知识点、技能、方法、数学思想,这些知识方法对自己而言是否是拦路虎,这道题还有没有其他解法,解法和结论是否具有普遍性,等等.有效的解题反思能帮助学生梳理知识和方法,提高学生解题能力,减轻学生学业负担,激发学生学习兴趣.本文拟从“一题多解”与“多题一解”的角度谈谈如何引导学生解题反思,将解题推向深入,努力让学生达到“做一题,通一类,会一片”的高层次境界.
一、一题多解,培养发散思维能力
吉尔福特提出:“发散思维是一种记忆的广泛搜索.”发散思维是指思维主体为完成任务或实现目标,充分发挥人的想象力,突破原来的知识圈,沿着不同方向,从不同角度思考,不墨守成规,不拘于传统方法,没有固定范围的局限,由一点向四面八方想开去,由已知探索未知的思维形式,是对同一问题探究不同的甚至是奇异答案的思维方法.
许多数学题重在考查学生思维的全面性、深刻性和灵活性,有多种解法.教学中引导学生从不同角度思考,最大限度调动学生思维的积极性,尽可能触及学生思维的“最近发展区”,适当点拨引导,让学生探索新的解题途径,将思维活动引向深入,获得成功体验.
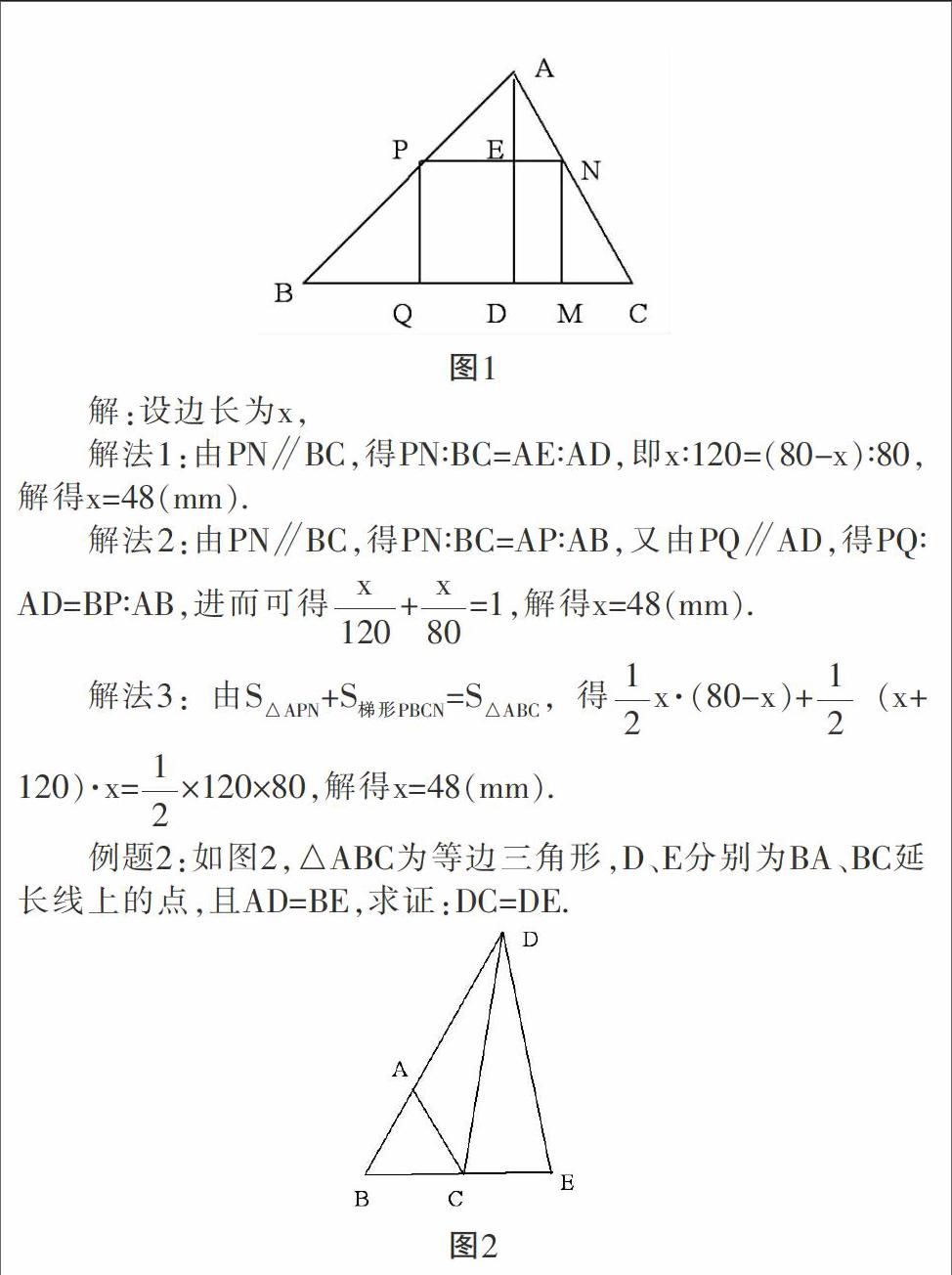
例题1:如图1,有一块三角形余料ABC,它的边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,问加工成的正方形零件的边长是多少?
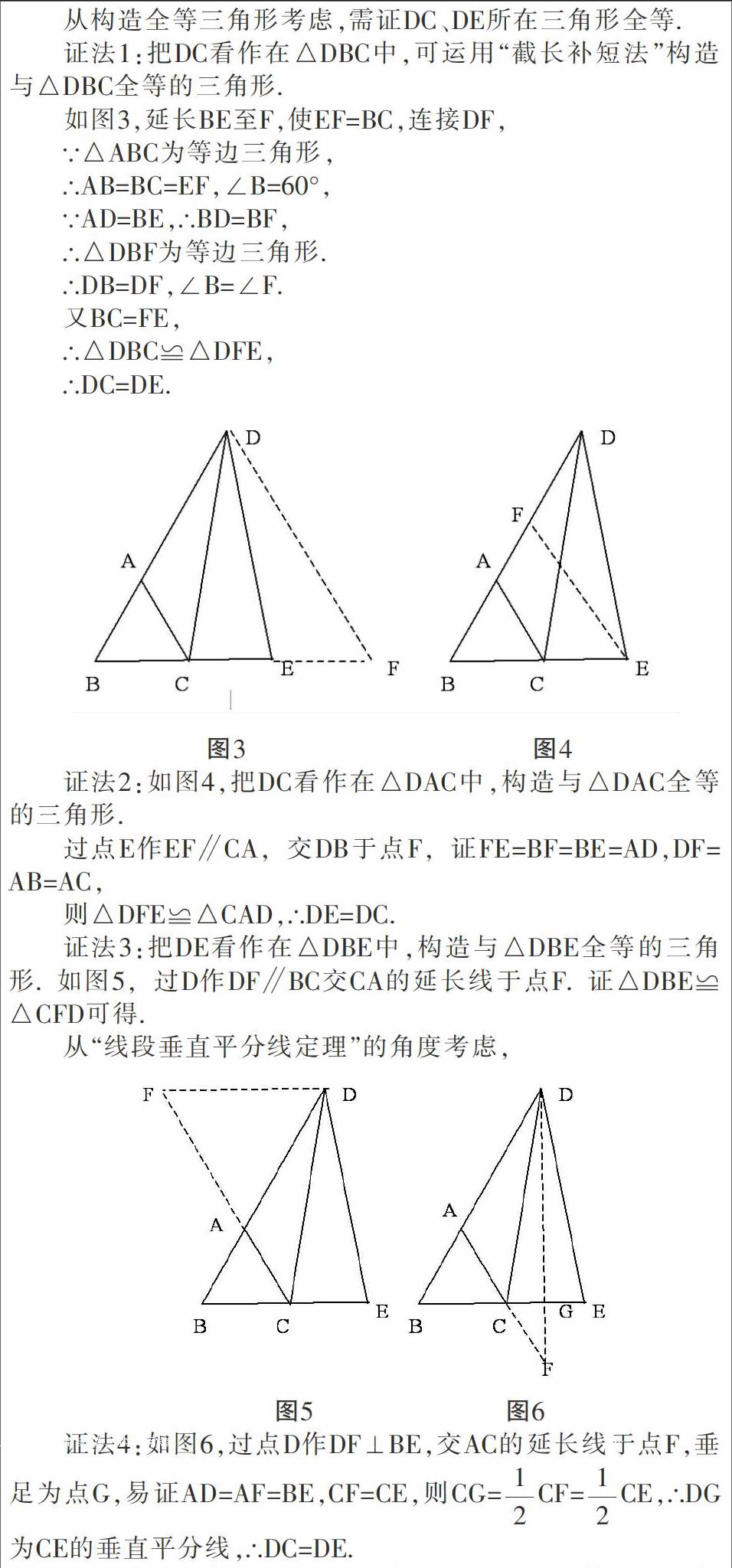
从以上证法中,根据所想用知识的需要进行构造是几何证明中添加辅助线的常见思维动因,如何添加辅助线,与我们解题时的思维切入角度有很大关系.
依据图形背景,联想所学定理进行构造也是添加辅助线常见思维动因,平时养成多角度思考的习惯,就能在许多看似平凡的地方发现很多不平凡的东西,让我们受益无穷.
二、多题一解,感悟知识联系
许多数学题看似不同,但它们的内在本质或者说解题的思路、方法是一致的.在教学中引导学生对这类题目分析、比较,寻求通法、通解,让他们抓住问题本质,感悟知识间的内在联系,培养学生求同存异的思维能力,形成数学思想方法.
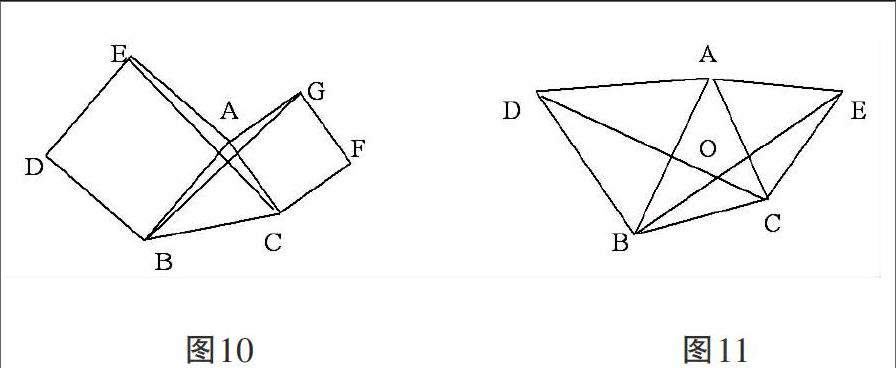
例题4:如图10,分别以△ABC的边AB、AC为一边向外作正方形AEDB和正方形ACFG,连接CE、BG,求证:BG=CE,BG⊥CE.
分析:证△ABG≌△AEC易得.
让正方形ACFG绕点A逆时针进行旋转,其余条件不变,画出几何图形,猜想以上结论是否成立?请说明理由.(用几何画板演示)
三、一题多解与多题一解实解题教学的注意事项
1.一题多解教学注意事项
首先要选好题,针对学生实际,选择具有典型性和代表性的题目,不宜太复杂,但也不能过于简单.过于复杂既挫伤学生研究学习的积极性,又不利于学生掌握方法,培养思维能力,过于简单学生没有兴趣,也达不到培养思维的目的.其次,在一题多解教学中,既要注意方法的多样性又要注意通法通解,把握好思维的开拓和知识方法的落实,如果一味追求多解法的新、奇、巧和深、广、透,就会造成学生数学问题解决活动的失度和失控,损失一题多解的解题过程对培养学生优秀思维品质的应有效能.另外,学生自我感悟很重要,老师要引导、点拨,在学生思维受阻将学生思维引向深入,突破思维上的一个个关节点,老师千万不能将一题多解变成自己的个人表演.
2.多题一解教学注意事项
多题一解教学中,选题时要注意题目与题目之间的关联性,要做到在形式上不同,与方法实质上的相同相统一.题目的呈现由浅入深,通过对简单题目的训练得到方法,再解决其他题目,感悟总结题目之间内在的和本质的联系.在这个训练过程之中,特别注意选题之间的关联性.多题一解是建立在“相同要素说”基础上的,这就要求各个题目之间要有相同的要素,而且是在实质上的相同.若是在形式上也相同,那么各个题目间就缺少区分度,这种训练不能达到由此及彼的效果;若是在实质上相去甚远,则训练也就毫无意义.
老师点拨归纳时,对几个问题实质的描述上要做到简洁一般.多题一解中的一般解法是作为一个通式,甚至一个规律出现的,对它的描述必然是简约的、抽象的,这样才能抓住各个题目之间解法的普遍性.
结语
课堂教学要体现“以学生发展为本”的教学理念,要求教师必须创造性地使用教材,创造性地设计学生活动.通过一题多解开阔学生思路、发散学生思维,让学生学会多角度分析和解决问题;通过多题一解,对相关知识进行有效的拓展和迁移,拓展学生的思维深度,分析事物时学会由表及里,抓住事物的本质,找出事物间的内在联系.
在教育教学工作中,教师要多注重挖掘解题过程对学生思维能力的培养,做到解答题目和训练思维能力两者兼顾.本文只是从一题多解和多题一解两个角度进行了阐述,还有很多解题过程可促进学生的思维能力的发展,这就需要广大一线教师和科研工作者进行更深入的研究和探讨.
