“基本问题和基本方法”理念下的“三角形解的个数问题探究”
2020-11-06侯木兰
侯木兰
[摘 要] 在高中数学学习阶段,许多问题可以归结为一些基本问题的衍生,许多问题可以运用一些基本方法得到有效解决,而数学核心素养的发展也扎根于“基本问题和基本方法”之中,所以,掌握“基本问题和基本方法”是一种值得选择的教学策略.
[关键词] 基本问题;基本方法;三角形解的个数?
解三角形问题是高中数学的基本问题之一,而求解不确定的三角形的解的个数问题又是解三角形问题中的常见问题. 学生往往在遇到这类问题的时候会觉得不易下手,或者会片面地认为只能用正弦定理解决,然后得到答案就草草了之,所以对这一问题的处理方式,不但影响到前期关于正弦定理、余弦定理的理解认知,而且还有可能造成学生记忆结论的被动学习状态. 本文以执教过的“三角形解的个数问题探究”教学片段为例,谈谈笔者对关于“基本问题基本方法”理念下的三角形解的个数问题的一些处理及思考,请同行指导.
案例片段呈现
1. 创设探究情境
引例(课前完成):△ABC中,a,b,c分别为A,B,C的对边,根据下列条件求解三角形:
(1)a=4,b=5,C=60°,求c;
(2)A=30°,B=45°,a=4,求c;
(3)a=4,b=5,c=5■,求C;
(4)①a=2■,b=■,B=30°,求c;②a=2■,b=■,B=30°,求c;
③a=2■,b=4■,B=30°,求c;④a=2■,b=■,B=30°,求c.
设计意图:让学生事先选择正弦定理或余弦定理求解三角形. 本节课开始通过设疑引导学生观察,归纳提炼三角形解的个数与条件中所给元素中边和角的关系.
2. 设问指向课题
教师:以上三角形分别有几解?相对应的已知条件中分别有哪些元素?
学生:(1)只有一组解,已知条件中的元素为两边及其夹角;(2)只有一组解,已知条件中的元素为两角及一边;(3)只有一组解,已知条件为三边;(4)中已知条件都为两边及其中一边所对的角,解的情况是:①只有一组解;②无解;③只有一组解;④有两组解.
教师:完全正确!那么对于任意一个三角形,如果给出与上题中相同性质的元素,是否都会与上题中的三角形有相同的解的个数?
学生:上题中已知基本元素都是3个. 对于任意一个三角形,当已知条件中的基本元素为两边及其夹角、两角及一边、三边时,都只有一组解,但当已知两边及其中一条边所对的角时,有可能有一组解,有可能有两组解,也有可能无解.
教师:其他同学同意她的说法吗?请一位同学来说说为什么.
学生:初中学习过全等三角形及其判定,对于已知两边及其夹角、两角及一边或三边的三角形,都是全等的,所以只有一组解. 当已知两边及其一条边所对的夹角时,我感觉应该是解的情况不确定,但我也不知道如何求证解的情况.
教师:请同学们再仔细观察引例(4),看看你能发现什么.
学生:我发现a和B都相同,只有b不同. 哦,那就是说随着b的变化,三角形解的个数发生了变化.
教师:在a和B不变化的情况下,是否只有引例(4)中的b会使得三角形得到以上解的情况?
学生:肯定不是.
教师:那么当已知a和B时,b取哪些值会使得三角形分别有两解、一解或者无解呢?
3. 探究过程
探究一(合作探究):△ABC中,已知a,B,b为何值时,三角形有两解、一解、无解?
设计意图:延伸引例中揭示的问题,探究已知条件为一边及另一边所对的角时,三角形解的个数与另一边的关系.
例1:已知△ABC中,a=4,B=30°,b为何值时,三角形有两解、一解、无解?
教师:请同学们说说你们的做法!
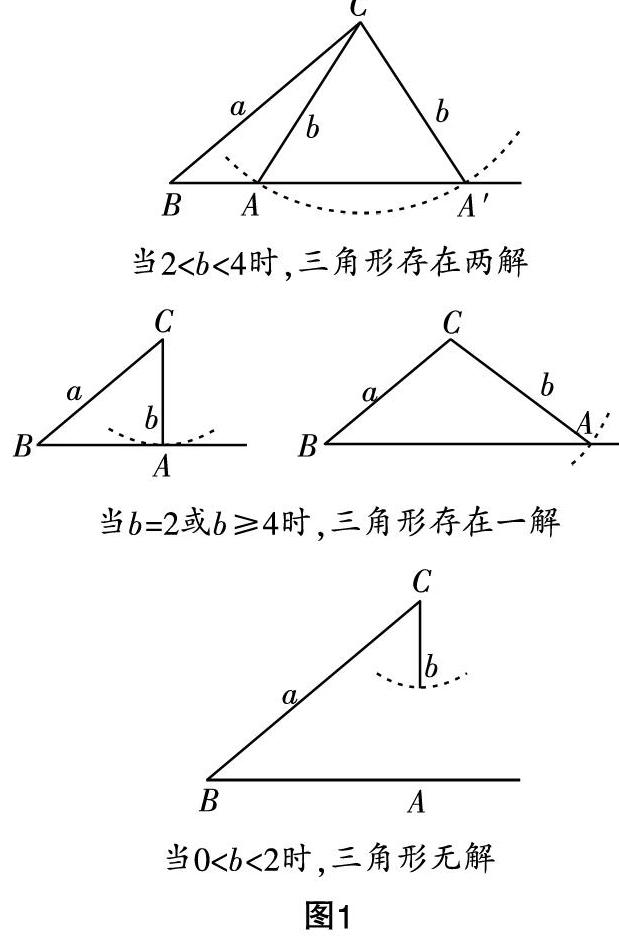
学生1:(方法一)我用的是正弦定理:由■=■,得■=■,所以sinA=■. 又B=30°, 所以A∈0,■π,当■
学生2:(方法二)我用的是余弦定理:由b2=a2+c2-2ac·cosB得c2-4■c+16-b2=0,视作c的一元二次方程,则Δ= (-4■)2-4(16-b2)=4b2-16. 当Δ<0,即0 学生3:(方法三)老师,我是画图做的.我先作角B,再作角B的邻边a,这样就确定了顶点C的位置,再作角B的对边b,即以C为圆心,b为半径画圆,观察圆弧与角C的对边c的交点的情况,那么有几个交点就对应三角形有几个解: 当2 当b=2或b≥4时,三角形存在一解 当0 教师:非常棒,我们为这三位同学鼓掌!解三角形问题的基本方法就是应用正弦定理或余弦定理建立方程进行求解. 对于方法一,在考虑解的问题时若能将sinA=■看作函数y=■与函数y=sinA,A∈0,■π的交点则更简洁清晰,此处也体现了数形结合的基本思想;方法二是借助余弦定理,把问题转化为方程的正根的问题,计算稍烦琐,但也体现了正弦定理与余弦定理的相通之处以及方程思想的灵活应用;方法三也是非常巧妙的方法,三角形作为几何图形,在解决相关问题时从图形的角度入手是非常自然的事情,只是在解答题上,还要配一定的符号说理方显严谨. 教师:请同学们思考,上述结论能否推广到任意的a,A和B?为什么? 学生:可以,推理过程如上. 当B为锐角时,若b 设计意图:由具体到抽象,锻炼学生的抽象概括意识,此题所得的结论并不需要学生记忆,重点在于这种探究总结的意识以及对于基本方法的掌握和灵活应用. 教师:如果改变条件呢?请同学们试用基本方法来解决以下问题. 变式:a=4,A=30°,b为何值时,三角形有一解、两解、无解? 解析:方法一:由■=■,得b=8sinB,又A=30°,所以B∈0,■π. 当■ 方法二:由a2=b2+c2-2bc·cosA得c2-■bc+b2-16=0,视作c的一元二次方程,则Δ=(-■b)2-4(b2-16)=-b2+64.当Δ<0,即b>8时,方程无实数根,三角形无解;当Δ≥0,即0 方法三:图解法(略). 设计意图:变式和例1本质相同,稍作改变,不可直接用上述结论,让学生再次体会掌握基本方法带来的重要,感受探究带来的乐趣. 探究二(自主探究——链接高考):通常用a,b,c表示△ABC的三个内角A,B,C所对边的边长,R表示△ABC外接圆的半径,给定三个正实数a,b,R,其中b≤a,问:a,b,R满足怎样的关系时,以a,b为边长,R为外接圆半径的△ABC不存在、存在一个或两个(全等的三角形算作同一个)?在△ABC存在的情况下,用a,b,R表示c. 解析:方法一:由正弦定理■=■=■=2R可得a=2R·sinA,b=2R·sinB. 当a=b时: 若a>2R,则sinA>1,与sinA∈(0,1]矛盾,故不存在三角形; 若a=b=2R,则A=B=■,与三角形内角和定理矛盾,故不存在三角形; 若a=b<2R,则0 当a>b时: 若a>2R,则sinA>1,与sinA∈(0,1]矛盾,故不存在三角形; 若a=2R,则A=■,故存在三角形且只有一个,c=■; 若a<2R,则sinA∈(0,1),sinB∈(0,1),则A∈0,■,B∈0,■,A>B或者A∈■,π,B∈0,■,即存在两个三角形,对应的c=■. 综上所述,当a>2R≥b或a≥b≥2R时,不存在;当a=b<2R时,存在一个,c=■■;当b 方法二:由余弦定理可得c2=a2+b2-2ab·cosC,將cosC=-cos(A+B)=-cosAcosB+sinAsinB=-■·■+■·■代入上式,两边平方得有关c2的一元二次方程(c2)2+■-2(a2+b2)c2+(a2-b2)2=0(?鄢),其中Δ=■-2(a2+b2)■-4(a2-b2)2=■(a2-4R2)(b2-4R2). 当Δ<0,即b<2R 当Δ≥0时,方程有实数根,不妨记方程的两根分别为c1,c2,由(?鄢)式易知c1·c2≥0. 若Δ=0,c1·c2=0,即a=b=2R时,方程有两个相等实根为0,三角形不存在; 若Δ=0,c1+c2>0,c1·c2>0,即a=2R>b时,方程有两个相等正根为c1=c2=a2-b2,三角形存在且只有一个,且c=■; 若Δ>0,c1+c2<0,即a>b>2R时,方程有两个不等负根,三角形不存在; 若Δ>0,c1+c2>0,c1·c2=0,即a=b<2R时,方程有两个不等实根,其中一根为c1=0,另一根为c2=■(4R2-a2),三角形存在且只有一个,且c=■■; 若Δ>0,c1+c2>0,c1·c2>0,即b 设计意图:本题中虽然给出的三角形的基本元素为两边及外接圆半径,表面似乎与例1及变式不同,但本质都是三角形解的个数问题,所以仍采用解三角形问题的基本方法,即使用正弦定理或者余弦定理建立方程,只是本题中因为b≤a所以需分类讨论a与b的关系,难度有所加大,但在前面例题的铺垫之下部分学生还是可以快速顺利解决的. 在讨论a与b的关系的基础上,再同例1和变式一样进行讨论,整个解决过程依旧彰显了基本方法的重要性;同时,也需要体会和能够自然地进行应用基本数学思想. 案例反思 基于“基本问题和基本方法”的理念,以上片段是笔者在关于“三角形解的个数探究”教学中的一点处理,呈现了“用正弦定理,再转化为函数的交点个数问题”“用余弦定理,转化为方程正数根的问题”“作图”的三种基本方法,展示了问题探究和方法提炼的详细过程. 实际上,含参的三角形解的个数问题并不简单,但是通过以上教学过程的设计与实施,还是能取得较好的效果,不仅可以促进学生夯实基础知识,强化基本技能,还可以领悟基本的数学思想. 在整个探究过程中获得数学探究活动的基本经验. 高中数学的学习离不开解题,但从数学试题的编制和考查来看,我们需要了解和掌握数学问题所涉及的基本概念,要了解试题包含的基本问题,要熟悉解决相应基本问题的基本方法,也许还要自觉运用一些基本的数学思想. 这是我们了解数学试题,乃至数学问题所涉及的“基础”. 所以在教学中需要老师善于引导学生把握问题本质,抓住解题关键,指导学生学会用数学眼光来发现甚至提出问题,用数学的思维来分析和解决问题,用数学的语言表达和阐述问题,促进学生在归纳概括基本问题和总结提炼解题基本方法的学习中,发展数学核心素养.
