《质数与合数》教学设计

李 冉

【教学内容】

青岛版五年级上册第六单元信息窗3。

【教学目标】

1.结合具体情境，理解质数、合数的含义，并能判断一个数是质数还是合数。

2.在探索新知识的过程中，渗透观察、猜想、验证等探索规律的基本方法。体验从特殊到一般的认识发展过程，使思维逐渐严谨。

3.通过探索活动，感受数学思考的条理性，发展初步的归纳、推理能力，激发探索规律的兴趣。

4.在研究质数与合数的过程中，加强对数学发展的认识，感受数学知识的魅力。

【教学重点】

理解质数和合数的意义。

【教学难点】

判断一个数是质数还是合数的方法。

【教学准备】

教具：多媒体。

学具：小方块、学习单、数字卡片。

【教学过程】

一、创设情境，提出问题

谈话：这幅图中的场景，你在哪里见过？今天这节课，我们就一起来研究一下方队中的数学问题。

（课件出示情境图）

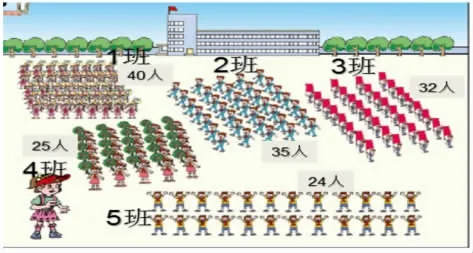
提问：你能发现哪些数学信息？

预设：一班方队有40人，二班方队有35人，三班方队有32人，四班方队有25人，五班方队有24人。

提问：说一说你理解的什么是方队？

预设1：排成方形的队伍，方方正正的队伍。

预设2：每行人数相同，每列人数相同。

追问：排成一行能叫方队吗？为什么？

预设：不行，是一条直线。

谈话：大家看，人数是 40、35、32、25、24 人的队伍，可以排成方队。

提问：观察一下，能排成方队的数有什么特点？

预设：偶数，5的倍数。

追问：我们来看一看这些数个位上的数，有没有共同特点？十位上有没有共同特点？

谈话：这就奇怪了，那能不能排成方队跟什么有关呢？会不会跟它们的因数有关呢？我们一起来看看吧。

（课件展示这些数的因数）

【设计意图：以“能不能排成方队”这一问题情境引入新课，借助学生熟悉的、常见的队列队形为载体来学习质数和合数，旨在现实生活中找到一个重要的数学模型。学生在分析问题的过程中，猜测是否能排成方队与一个数因数的个数有关，初步感受到质数、合数的本质，从而引入新课的学习。】

二、合作探索，理解概念

1.引导猜想。

提问：仔细观察，这些数的因数有什么共同特点？

预设：除了1和它本身之外，还有其他因数。

谈话：大胆猜想一下，什么样的数可以排成方队？

预设：除了1和它本身还有其他因数，也就是因数的个数是两个以上的数，就可以排成方队。

追问：但是仅凭这几个数能证明这个猜想吗？那该怎么办呢？

2.验证猜想。

谈话：下面我们就来研究一下1～10这十个数。

小组合作1：

（1）用小方块依次摆一摆1～10这十个数，探究哪些数不能排成方队，哪些数能排成方队。

（2）组长把结果记录在《学习单》上。

（学生小组合作，动手验证自己的想法）

（教师进行巡视，适当指导）

（课件出示摆小方块的过程）

提问：4怎么排的？每行几个？排了几行？6怎么排的？8怎么排的？9怎么排的？10怎么排的？

整理：不能排成方队的有：12357

能排成方队的有：468910

追问：接下来我们该研究什么了？

预设：它们的因数个数。

小组合作2：

（1）找出这两组数的因数，记录在《学习单》上。

（2）仔细观察，你们能发现什么？把你们的发现记录下来。

3.汇报结果。

谈话：哪个小组来展示一下你们的结果？

预设：我们发现不能组成方队的数，因数只有1和它本身，1只有1个因数。能组成方队的数，因数除了1和它本身还有其他的因数。

三、对比发现，总结概念

谈话：我们再一起来整理一下。

（课件出示）

板贴：只有1和它本身两个因数，这样的数叫质数，也叫素数。

追问：接着看，这些数都能排成方队，它们的因数都有什么特点？

板贴：这些数除了1和它本身还有其他的因数，我们把这样的数叫做合数。

追问：老师刚才悄悄擦掉了一个数，你发现了吗？那么1是质数还是合数呢？为什么？

板贴：1既不是质数，也不是合数。

【设计意图：通过组织学生观察、猜想、验证，从而发现了质数和合数的本质属性，得出概念。接着引导学生去比较、辨析发现新的规律：关于质数和合数的区别及1的分类问题。这样不仅能提高学生对概念的理解，而且能拓展学生对概念的内涵与外延的把握。】

四、拓展练习，应用概念

1.举例巩固。

谈话：谁能举个质数的例子。对吗？谁来举个合数的例子？

（学生举例判断）

谈话：老师出一个数，你们判断一下它是什么数。好吗？

16 7 53 85

追问：为什么判断这么快？

总结：2、3、5的倍数，除了它本身都是合数。

2.合作巩固。

小组合作3：

用自己手中的数字考一考其他同学，判断这个数是质数还是合数，并说明原因。

活动：小组合作上台当小老师，考一考全班同学。

3.类比巩固。

活动：根据要求举起你手中的数字。

（1）请把偶数举起来。

（2）请把奇数举起来。

追问：有没有没举起来的呢？为什么没有？偶数和奇数是怎样来区分的呢？

总结：根据是不是2的倍数，我们把自然数分成了奇数和偶数。

（3）请把质数举起来。

（4）请把合数举起来。

追问：有没有没举起来的呢？质数和合数是怎样来区分的呢？

总结：根据因数的个数，可以把非零的自然数分成质数、合数和1。

4.火眼金睛辨对错。

（1）一个非零自然数，不是奇数就是偶数。（）

（2）一个非零自然数，不是质数就是合数。（）

（3）大于2的偶数都是合数。 （）

（4）所有的质数都是奇数。 （）

【设计意图：运用不同的形式，选取不同层次类型的题目，加深认识，达到对知识的熟练和灵活运用。同时设计互动活动，旨在沟通知识之间的联系，知道数的分类标准不同，结果不同，把握知识的来龙去脉，知道知识的生长点和延伸点，培养举一反三的能力。】

五、回顾整理，提升认识

谈话：同学们，这节课的知识学完了，我们一起来回顾一下，我们是怎样来进行学习的呢？

课件出示回顾整理：

谈话：在这个过程中，大家经历了“猜想—验证”的过程，这是一种非常重要的数学方法，所有伟大的数学发现，都是从猜想开始的，今天，老师给大家带来了一个有趣的猜想。

介绍哥德巴赫猜想和陈景润。

【设计意图：通过回顾整理，梳理整节课的思路，通过学生阅读资料，使学生真切感受到数学的魅力与价值，增强他们学习数学的兴趣和信心。】