现代“小先生制”下的课堂教学新样态——以《长方体和正方体总复习》一课为例

沈 君

“小先生制”是著名教育家陶行知先生在普及教育实践过程中依据“即知即传人”的原则，采取“小孩教小孩”、“小孩教大人”的方法，倡导并推广实施的一种教学制度和儿童学习制度。

现代“小先生制”是指在新时期教育背景下，以陶行知“小先生制”学习制度为思想精髓，在课堂教学中依据学生不同的知识、能力水平和品质特征，在自主学习的前提下，充分发挥个体特长，通过多主体互助合作，以达到共同进步的教学制度。

基于以上思考，笔者在《长方体和正方体总复习》一课的教学设计中，立足于现代“小先生制”课堂教学新样态的理念，以生为本，学为中心，充分发挥学生的主体性。

【教学过程】

一、复习正方体的棱长、表面积、体积

师：王叔叔最近想为自己家做一个正方体的柜子。要求是：正方体的棱长总和是72分米。你可以求出它的什么？还能求出什么？

生：棱长、底面积、表面积、体积、容积等。

师：这几个问题我们要先求出什么？（棱长）请同学们在《作业单》上算一下它的表面积和体积。哪个小组愿意派一名小先生来说一说？

生：72÷12=6（分米），6×6×6=216（平方分米），6×6×6=216（立方分米）。

师：观察后面两个算式，我们能不能说正方体的表面积和体积一样，都是216？

生：不能，因为正方体的表面积和体积是不能比较的。

师：是的，表面积指的是正方体面的大小，体积指的是正方体所占空间的大小，尽管得数恰好一样，但它们表示的意思并不一样。

二、复习长方体的表面积、体积

师：这么一算，王叔叔发现这个正方体柜子小了一些，于是就做成了这样，是什么形状？

师：这个长方体的长、宽、高分别是多少？体积是多少？你会求它的表面积吗？请你在作业单上算一算。想一想还有没有不同的算法？做完的同学在小组里交流一下。

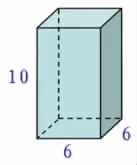
师：哪一组同学愿意做小先生上来跟大家说说你们小组的算法？

1.交流算式，体会算法多样化。

（1）（6×6+6×10+6×10）×2=312（平方分米）。

（2）6×6×2+6×10×4=312（平方分米）。

（3） 6×6×2+6×4×10=312（平方分米）。

2.对比算式，理解算法并优化。

师：为什么第（2）个算式可以这么简便？你能具体说一说吗？

生：6×6×2 算的是上下两个面（正方形）的面积，6×10×4求的是长方体前、后、左、右四个侧面的面积。

师：比较（2）、（3）两个个算式，6×4×10 与刚才的 6×10×4 一样吗？

生：不一样，6×4指的是底面周长，底面周长×高就是侧面积；6×10指的是一个侧面的面积，再乘4就是4个侧面的面积。

师：说得真好！我把它的表面积展开，谁来指一指6×4求的是哪儿？再乘10呢？这样就把它侧面的四个小长方形转化成了一个大长方形，那么，6×4其实就是大长方形的长，原来的高10就是大长方形的宽，对吗？

三、联系生活，理解长方体表面积的实际应用

师：王叔叔想给这个柜子刷上漂亮的油漆。凭你的生活经验，你觉得应该刷多大面积的漆呢？求刷漆的面积实际上是求长方体的什么？你认为该怎么刷呢？下面小组讨论，只列式不计算。

师：哪一组同学愿意做小先生来跟大家说说你们小组的算法？你的算法是求了几个面的面积？哪个面没刷？为什么可以不刷？

小结：一般求长方体表面积时6个面都算。但是在生活中要具体问题具体分析。

四、联系生活，解决长方体组合图形的表面积

师：王叔叔最后决定要把这两个柜子做成这样的组合柜（见下图），而且是背面靠墙。现在王叔叔想请你们帮他想一想，如果给这个组合柜刷漆，既要美观又要尽可能节约成本，你觉得应该刷哪些面呢？

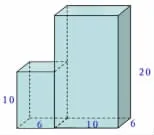
师：哪一位小先生愿意来说一说你们小组建议王叔叔刷哪些面？其他面为什么不刷？

师：这些面的面积你会算吗？请大家只列式不计算，想一想，算这些面的时候有没有更简便的方法？

生 1：20×10+20×6+10×6+10×6+10×6+6×6 。

生 2：20×10+20×6+10×6×3+6×6。

生 3：20×10+20×6×2+10×6+6×6 。

生 4：（10+6）×20+6×2×10+（6+10）×6。

生 5：（10+6+6）×20+（10+6）×6。

小结：我们在算面积的时候可以把有联系的面合在一起，这样算就变得简单多了。

五、长方体的体积、容积的实际运用

1.小柜子里放长方体。

师：现在柜子刷好了，王叔叔可以往里面放东西了。请问放东西是跟柜子的什么有关？

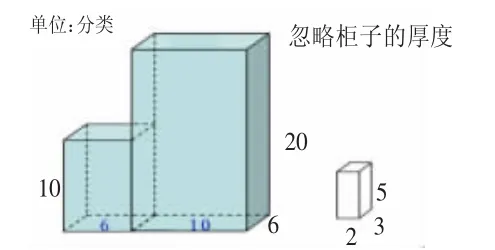
生：容积。

师：如果忽略柜子的厚度，在小柜子里放这样的小长方体，请问最多可以放几个这样的小长方体？请你在《作业单》上试一试。谁来说一说算式？你是怎么想的？

【方法一】小柜子容积除以小长方体的体积。

生：（10×6×6）÷（2×3×5）=12（个）。

【方法二】分别算出小柜子的长、宽、高里面各有几个小长方体，再相乘。

生：（6÷2）×（6÷3）×（10÷5）=12（个）。

2.大柜子里放长方体。

师：如果在大柜子里放这样的小长方体，（忽略柜子的厚度）最多可以放几个？在《作业单》上试一试。

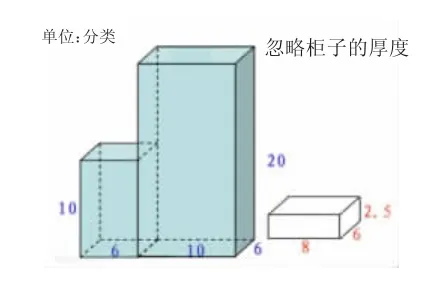
【方法一】大柜子容积除以小长方体的体积。

生：（20×10×6）÷（8×6×2.5）=10（个）。

师：说说你是怎么想的？

生：用大体积除以小体积计算的，结果是10个。

【方法二】横着放入柜子。

师：还有别的答案吗？柜子里一定能放得下10个小长方体吗？

生：大柜子的长是10分米，小长方体的长是8分米，我把小长方体横着放，这样就用大柜子的高除以小长方体的高，20÷2.5=8（个），可以放 8个。

师：旁边的空隙还能再放吗？

生：不能，剩下2分米，而小长方体最短的边是2.5分米。

师：这种方法只放进8个，还有其他放法吗？

【方法三】竖着放入柜子。

生：还可以竖着放。

师：如果竖着放，一排可以放几个？可以放几排？

生：每排4个，放2排，放了8 个，10÷2.5=4，4×2=8（个）。

师：还可以放吗？

生：还可以放1个。20-8×2=4，4÷2.5≈1，8+1=9（个）。

师：在实际生活中，我们往柜子里放东西的时候，往往会受到物体形状的影响，有时会造成一定的空间浪费。

六、课堂小结（略）

【课后反思】

本节课通过学生的提问、交流、评价,找到多种解决问题的策略，很好地培养了学生的思维灵活性，并且在灵活解决问题的过程中，强化了图形特征，渗透了转化思想。

在这个案例中，从学生已有的知识以及学生熟悉的生活情境和感兴趣的具体事物出发，通过实物、教具引导学生在理解的基础上掌握知识，给学生充分观察和实际操作的机会，让学生参与到获取知识的过程中，将抽象的知识变成了学生能看得见、摸得着的现实东西，使学生在观察和操作中，对知识的思考与实物模型的演示和操作有机地结合起来，在学生头脑中形成表象，建立概念，以动促思。在多种算法的交流中，选择适合自己的算法,不但调动了学生学习的积极性，更有助于学生形成探索性学习方式。