借力现代技术丰富学习方式
——新思维-魔数APP助力课堂教学
2019-01-07陈敏
陈 敏
以张天孝老师编著的《新思维儿童数学》为蓝本,浙江省新思维教科院核心教研团队与浙江魔数教育科技有限公司成立专项项目组,合力开发在线儿童数学教育产品,致力于让更多的儿童共享优质的数学教学资源。经过大家共同努力,取名为“魔数精灵可可”的APP项目正式上线。
一、独特、关联的思维训练体系
张天孝老师60余年在儿童数学课程开发领域独树一帜,孜孜以求,形成了一套别具一格而又行之有效的数学思维训练体系。借助这套体系,“魔数精灵可可”着眼于整个义务教育阶段数学内容的“前有铺垫、中有突破、后有发展”,精心编排内容结构,合理规划学习序列,有利于学生自主学习、发挥潜能。

图1.认识1-5(榨汁机游戏)
以“5”的相关知识为例。第一节相关课,“认识1~5”。课程任务之一“榨果汁”,具体要求:选择相应数量的水果放进榨汁机,并拨动算珠开关,启动“榨汁”。此处,实质是借助“算盘”作为认数工具,体会、强化“1”是自然数的基本单位,自然数表现为相应个数的“1”的累积。
第二节相关课,“认识6和7”。任务之一“整理糖果”,要求:选择相应数量的糖果罐头放入橱柜,并拨动算珠锁住橱柜。此处涉及到数群“5”的问题。游戏演绎如下:先由阳阳(剧中男孩)抢着放入5罐果蜜,并拨动5颗下珠,成功上锁;继而阳阳放入6罐蜂蜜,并遇到问题:下珠只有5颗,如何锁柜呢?比较物品,蜂蜜比果蜜多1瓶,6比5多1,因而想到在5颗下珠的基础上,再拨下1颗上珠,然而柜子发出警报声,锁柜失败。阳阳的操作过程代表了一般儿童思考的过程,具有相当的合理性。我们假定学生会有共鸣,并产生“那怎么办?”的疑问。停顿几秒后,另一位剧中人物“精灵可可”呼应提出:我知道,娜娜老师说过,可以用1颗上珠表示5。从前期的“按个计数”过渡到“按群计数”:6比5多1,可以拨下1颗上珠,再拨上1颗下珠。接下来,剧中人物招呼儿童:小朋友,一颗上珠表示5,请你帮助我们放好这些糖果,记得锁上柜门哦!
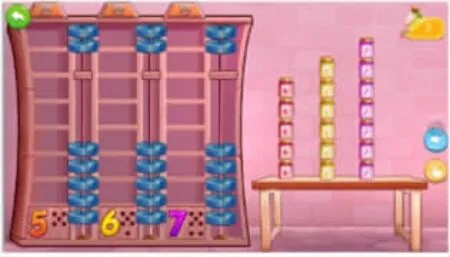
图2.认识6和7(储存糖果罐头)
第三节相关课,“认识8和9”。除了课程中包含以“5”为群计数的内容,课后还安排教唱“手指舞”(模拟算珠,用大拇指表示“5”,其余手指表示“1”,演示 1~9)。
第四节相关课,“两5凑10”计算20以内进位加法——
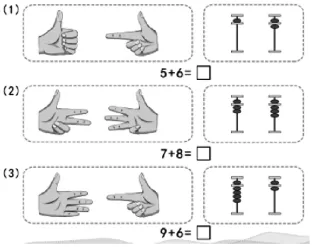
图3.两5凑10
至此,借助算盘,刺激、促发按群计数和简单计算的作用似乎昭然若揭,但我们想进一步明确:用算盘认数、用手指计算,并不仅止于“有趣”“传统文化”“算法多样”之类的目标,核心的立意是发展思维。在“两5凑10”这节课中,安排了以下任务,有心的学生应能认识到其中的联系——
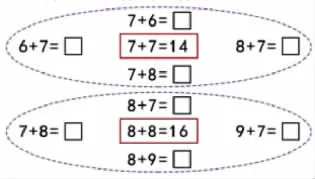
通过“两5凑10”,最重要是引进“推算”的思维经验,根据“5+5=10”的事实,可从加数中分拆出“5+5”,再将剩余部分合计为和的个位,如7+8=5+2+5+3=(5+5)+(2+3)=15。类似的,如果头脑中已有“7+7=14”的事实,那么“7+6”就不需要再重新计算,通过比较“7+6”与“7+7”,可以得出7+6=7+7-1=14-1=13……这些比较、分拆、重组、转化的活动,无疑大大丰富了计算活动的思维内涵,把按规定程序计算变成了灵动的推理,切实地在培养学生思维的灵活性、批判性和创造性。
总之,课程通过重组结构,使学生有更多的机会主动基于概念,开展逻辑推理活动,“再创造”数学知识和数学方法,以发展高层次思维,培育创新人格。
二、有趣、有效的数学问题情境
对于情境的研究告诉我们,好的情境不仅能够刺激学生的相关经验,促使他们主动发现问题和提出问题,还能直观、有效地支持学生思考问题的本质,帮助他们分析问题和解决问题。同时,我们认同,能在不同情境中运用数学、解释数学,是一个合格的未来公民所必需的数学素养。
“精灵可可”在情境设计方面投注了大量的精力。目前的情境设计虽不甚完美,但在趣味性和数学性方面还是可圈可点。每一节课都是一个相对完整的、富有童趣的故事,并力求与数学知识发生、发展的逻辑过程相契合。以第五节“认识8和9”为例:
巴度弄乱书柜,被发现;主人公阻止巴度,并帮忙整理。首先要数清书的本数,阳阳自告奋勇,1本1本认真数起来,娜娜老师提醒阳阳可以先数出5本,再作比较;引导认识8=5+3,9=5+4。
主人公把数清的图书放入书柜,引导观察:从左到右,5—9,逐个增加 1;从右到左,9—5,逐个减少1.从相邻数之间关系的角度再次认识8和9。引导拨动算珠,关闭柜门,借助算珠直观,巩固8、9 与 5、6、7 的关系。发现巴度偷走图书馆钥匙。
巴度逃跑,破坏桥板。主人公赶到后,引导修桥,学习8的分解和组成。拼接完成后,引导观察:从左到右,绿色桥板逐一减少,黄色桥板相应逐一增加,总量都是8块,渗透有序思考,渗透和不变的规律(函数观念)。
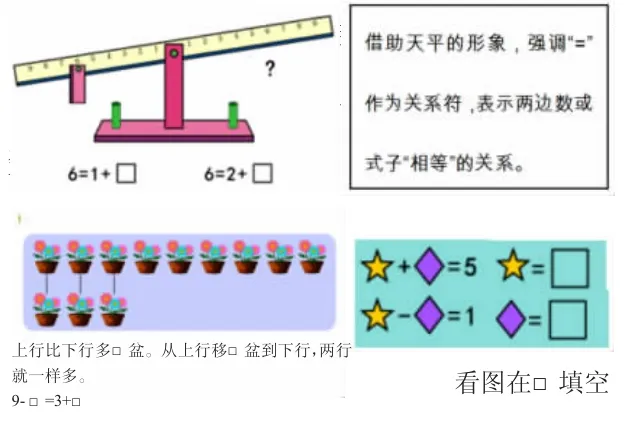
课程力求将有趣的情节和数学的本质融合在一起,构成有利于启发思考、帮助思考和推进思考的数学问题情境,让人机之间围绕情境互动,自然、自主、自觉地学习。
三、丰富、灵活的问题设计
张天孝老师一贯主张:小学生数学思维训练,不是数学知识的提前下放,也不是加快教学进度,而是在所学知识范围内,在知识应用的深度、广度和灵活度上下功夫。“精灵可可”课程使用了《新思维儿童数学》中大量新颖、有趣、层次丰富的数学问题。如代数特色问题——
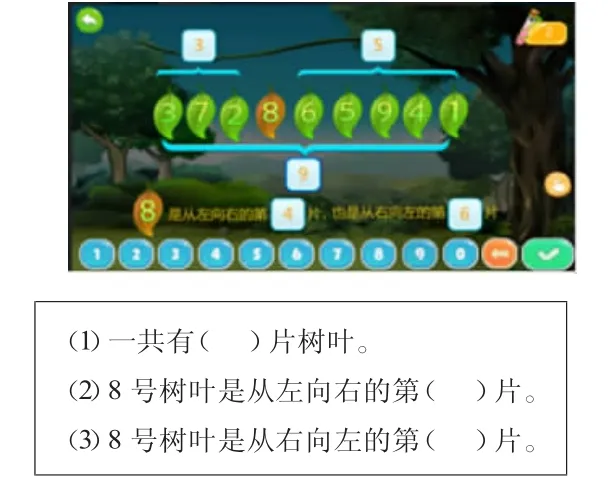
考虑到人机对话的产品特质,有些在情境和互动方面还做了进一步的挖掘和改造。如“几和第几”一课中安排有一组题,提了一系列相关联的问题——
先由学生独立填写,进而围绕第(3)问引导、交流不同的思考方法。阳阳的想法最普通:从右向左数数,得到答案,8号树叶是从右向左的第6片;琪琪能综合运用前两问的结果进行推理,一共有9片树叶,8号树叶是从左到右数的第4片,也就是到8号树叶为止一共有4片树叶,所以8号树叶右边还有5片树叶,8号树叶是从右到左数的第6片;可可的想法与琪琪类似:一共有9片树叶,8号树叶是从左到右数的第4片,也就是到8号树叶左边有3片树叶,所以从右数到8号树叶有6片树叶,8号叶是从右数起的第6片。琪琪和可可的思考体现了基数和序数意义的灵活转换,示范了多元解读条件信息的思维习惯。同时,这一系列问题可引发进一步的思考:从左数起,8号树叶是第4片,从右数起,8号树叶是第6片,那为什么一共不是10片而是9片呢?……
除了基本课程,“精灵可可”还设有“可可充电站”和“怪兽屋”栏目,分别对应不同的学习和练习需求。“可可充电站”配置有基本的技能训练、数学史小故事、折纸、手指舞等趣味数学活动等;“怪兽屋”则专供学有余力的学生挑战综合难度更高的数学问题。在解决丰富多彩的数学问题的过程中,帮助学生感悟数学概念和原理,积累各种思维经验,锻炼克服困难的意志,体验成长和进步的快乐,促成学生数学思维尊重个性地、有差异地发展。
