设计变式任务促进学生学习——《三角形的面积》教学实录与评析

吕琼华

【教学内容】

浙教版五年级上册第66、67页。

【教学过程】

一、情境引入

师：仔细观察下图，你能得到哪些数学信息？

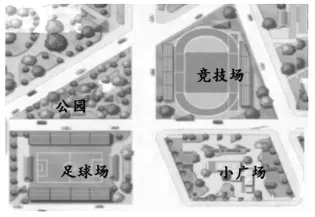
生：我看到许多平面图形：公园是三角形，足球场是长方形，竞技场是四边形，小广场是平行四边形。

（教师依次画出抽象图形）

师：如果和面积单元结合起来，你能计算哪几个图形的面积？

生：我能求出长方形和平行四边形的面积，不过需要知道图形的底和高的数据。

教师依次在抽象出的图形上标出数据——

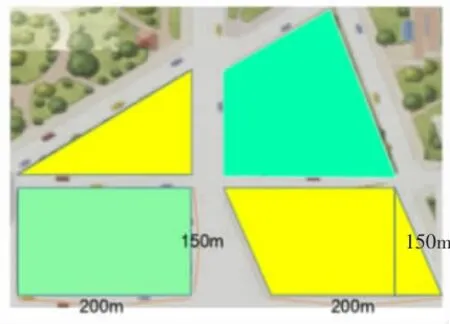
师：长方形面积怎么求？平行四边形呢？

生：长方形面积=长×宽，足球场的面积是：200×150=30000（平方米）。

生：平行四边形面积=底×高，小广场的面积是：200×150=30000（平方米）。

师：大家还记得我们是怎样研究平行四边形面积的吗？

生：沿平行四边形的高线切割，平移再拼成长方形。

师：为什么要把平行四边形转化成长方形？

生：长方形的面积已经学过。

师：原来研究时是把未学习的新图形转化成已经研究过的图形。（板书：转化）那转化成的这个长方形和原来的平行四边形有什么关系呢？

生：同底、同高、面积也相同。

（根据学生回答板书：面积相同、同底同高）

师：非常好，我们研究新图形的时候经常是通过将新图形转化成已知图形，寻找新旧图形间的关系，来推导出新图形的面积计算方法。

师：现在还剩三角形和四边形，你建议先研究谁呢？为什么？

生：先研究三角形，因为四边形可以分割成两个三角形。

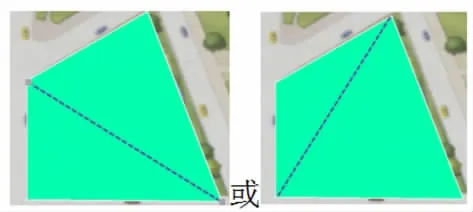
师：看来研究了三角形面积，就可以计算出这个四边形的面积了，你们的想法很不错。

二、研究直角三角形

1.研究三角形面积。

师：你会求平面图中这个三角形的面积吗？

生：这个三角形的面积很好求，就是足球场面积的一半。

师：这是一个——

生：直角三角形。

师：如果我们先研究直角三角形，你们可以自己独立研究吗？老师为大家准备了一幅图，图中每个小正方形的边长为1，请研究图中直角三角形的面积。请你写一写、画一画，说明你的想法。

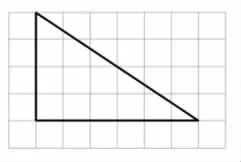
（学生独立活动，教师巡回、收取典型作品）

2.交流研究方法。

（1）倍拼法。

师：大家能看懂这位同学的方法吗？

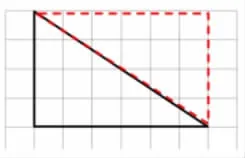
师：你能从这三方面（板书：转化 关系 面积）来说一说他是怎么研究的吗？转化成什么图形？转化前后的图形面积、底、高之间有怎样的关系？所以这个三角形的面积可以怎样计算？

（2）等拼法。

师：谁能从三方面来说一说这个研究方法？

师：看这里有一份方案，你们有什么想说的吗？

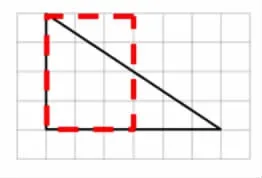
生：其实他俩想法差不多，都是转化成长方形。

生：不同的是一个是取了高的一半，所以算法是底×（高÷2），另外一个是取了底的一半，算法就是（底÷2）×高。

相同：都转化成了长方形的面积；

不同：高÷2（半高）

底÷2（半底）。

师：黑板上有三种不同的方法，你能来分分类吗？为什么？

生：我建议分两类：一类是转化成面积是2倍的长方形，一类是转化成面积一样的长方形。

生：我也觉得分两类：一类是拼上一个完全一样的三角形；另一类是取自己底或高的一半割下来补成长方形。

教师引导学生定名：倍拼法、等拼法。

3.回顾小结。

师：这些方法有什么相同的地方吗？

生：无论是哪种方法，都是将直角三角形转化成了我们学过的长方形来研究面积的计算方法。

师：现在我们已经知道了直角三角形的面积是怎样计算呢？

生：底×高÷2。

师：这个公园的面积是？

生：200×150÷2=15000（平方米），公园也挺大的。

师：下一步我们来研究什么？在研究前你有什么猜测？

生：是不是三角形的面积都等于底×高÷2？

生：是不是三角形的面积都可以用倍拼法和等拼法来研究？

三、研究锐角三角形和钝角三角形的面积

1.明确研究要求。

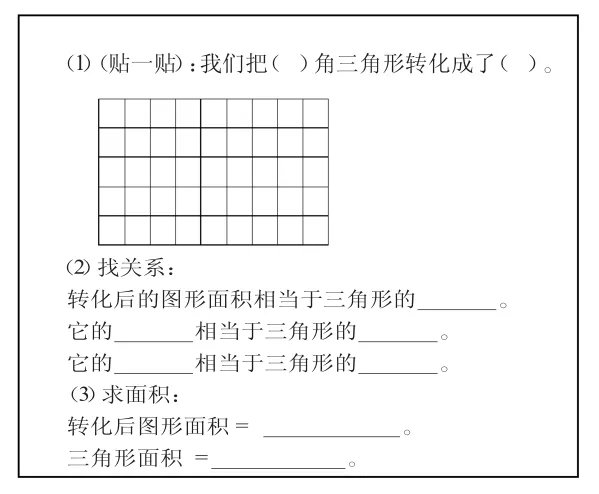
研究形式：同桌两人一组合作研究。

研究内容：选择一种三角形进行研究。

研究材料：练习纸中的方格纸和信封中的三角形（为了研究方便，每一种三角形都多打印了几份，只需要选择其中的一种进行研究就可以了）。

研究过程：按照练习中的提示研究，做好观察、思考和记录。

2.分组研究。

3.交流反馈。

（1）锐角三角形。

组1：倍拼法。

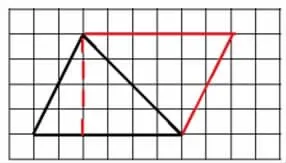
生：把两个完全一样的锐角三角形拼成一个平行四边形。平行四边形的面积就是三角形面积的2倍，平行四边形的底就是锐角三角形的底，平行四边形的高就是锐角三角形的高。

转化后图形的面积=底×高

↓

三角形的面积=底×高÷2

师：有问题吗？除以2是什么意思？

生：“除以2”是因为先前算的“底×高”是一个平行四边形的面积，这个平行四边形的面积是三角形的2倍，所以要“除以2”。

师：解释的非常清楚。组1的这一段推理也环环相扣，非常精彩。还有不同的方法吗？

↓

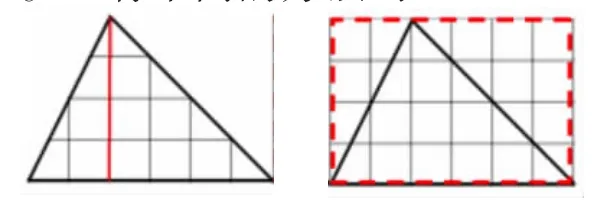
转化成学过的图形——面积倍拼

组2：等拼法。

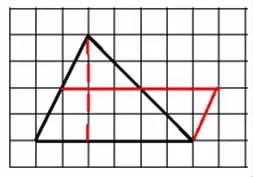
生：我们找到高的一半，画底边的平行线，然后把上面的三角形旋转下来，拼成一个与原三角形面积相等的平行四边形。平行四边形的底就是锐角三角形的底，平行四边形的高是锐角三角形高的一半。

转化后图形的面积

=底×（高÷2）

↓

三角形的面积=底×高÷2

师：大家觉得怎么样？

生：都是转化成平行四边形，这种转化方法使平行四边形面积与三角形面积相等。

师：那为什么还要除以2？

生：因为现在的高是原来的一半，其实是高除以2。

生：那我想到也可以底来除以2。我可以上来画一下吗？

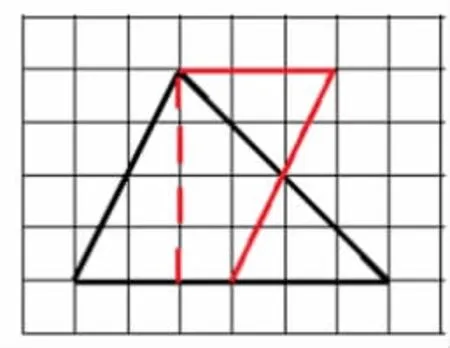
师：大家能明白吗？

转化后图形的面积

=（底÷2）×高

↓

三角形的面积=底×高÷2

师：通过研究发现，锐角三角形的面积怎样计算？

生：锐角三角形的面积=底×高÷2。

（2）钝角三角形。

师：那钝角三角形的研究结果如何？（课件呈现收集到的典型方法）同学们看看你们属于哪一种？或者现在你看懂了哪几种？

重点讲评：这里有一种不一样的方法——

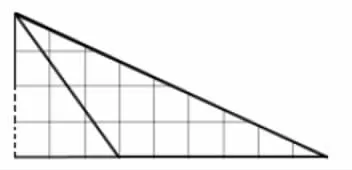
两个直角三角形面积相减

↓

转化成学过的图形

4.归纳三角形的面积公式。

师：仔细观察直角三角形、锐角三角形、钝角三角形的研究过程和结果，你有什么发现？

生：三角形面积=底×高÷2。

生：转化时，都用到了倍拼或者等拼的方法。

生：三角形的面积是和它等底、等高的平行四边形面积的一半（长方形是特殊的平行四边形），所以平行四边形面积是底×高，三角形面积是底×高÷2。

生：不同的转化方法，公式一样，其实含义不太一样，“÷2”可能是面积除以2，也可能是底或高除以2。

师：同样的结论有不同的解释。刚刚大家从知识的角度做了分析，那大家看看我们研究的过程，有没有什么值得分享的？

生：我觉得我们从直角三角形开始研究很明智，因为直角三角形一看就是与它等底等高的长方形的一半，面积好算，而且直角三角形研究出来了，锐角三角形和钝角三角形都可以仿照它来研究。

师：就是说遇到困难时，可以给图形分分类，从比较特殊的、容易研究的开始。

四、总结

师：今天我们从比较特殊的直角三角形开始，研究了各类三角形的面积算法，不仅知道了三角形的面积计算方法，而且知道了为什么是底×高÷2。

生：我们还得到了一些研究的方法——倍拼法、等拼法。

生：研究图形可以从特殊图形开始。

【编辑点评】

吕琼华老师的这一篇设计，较为突出的特点是能够通过前后有逻辑联系的学习任务，层层递进地支持学生自主探索、掌握三角形的面积计算方法，为学生增加了学习和表现的机会。

顾泠沅等人指出中国教师常常在教学过程中使用过程性变式，以推动学生有效地找到解决问题的方法。吕老师这节课例的四个任务即可理解为一组过程性变式。

首先，吕老师创设了一个计算社区活动场所面积的问题情境，情境中的平面图形经过精心设计，图形和图形之间有着特殊的联系，一方面可用以复习本节课的基础知识，包括面积的概念、长方形、平行四边形的面积计算、转化的思想等等；另一方面，引出了三角形面积计算的问题，特别是突出了直角三角形的面积计算。其次，基于对学生认知基础的了解（前测表明，学生普遍容易将直角三角形和相应的长方形面积相联系），并辅以情境图的直观支持，教师大胆下放直角三角形的面积探索任务。在反馈时，注意了两个层面的要求：从知识上，概括出直角三角形面积=底×高÷2，为进一步概括三角形面积公式指示方向；从方法上，整理、分类得到倍拼法和等拼法，为进一步探索锐角三角形和钝角三角形的面积做引导。在此基础上，引发更大范围和更深程度的学生有效参与，学生在锐角三角形和钝角三角形的探索活动中，深入体验和反思三角形的面积推导方法、逻辑表达及算法意义，优秀的学生还可以进一步创新方法，联通比较，形成更高程度的对知识和方法的概括。整个教学设计环环相扣，行云流水、质朴扎实，可以看做有指导的探索活动的一种范式。