质数“嫌疑犯”

托托

质数怎么成了“嫌疑犯”了呢？呵呵，这不过是一个风趣的说法。质数又被称为素数。在自然数里，质数是除了1 和它本身外，无法再分成两个整数相乘形式的整数。等一等，什么是自然数？自然数就是0，1，2，3，4……它们都是整数，一直数下去是数不完的。

那为什么要把质数单独拿出来呢？因为质数在数学家们的眼里，是非常有研究价值的，他们为此孜孜不倦，甚至耗尽毕生精力。你应该听说过“哥德巴赫猜想”吧，它被誉为数学皇冠上的明珠，也是和质数相关的。哥德巴赫猜想可以简单地表述为：是否每个大于2 的偶数都可写成两个质数（素数）之和？

我们随便找一个100 以内的质数来研究一下吧。比如23 就是一个质数，因为除了1 和23 之外，没有哪个整数能够将它整除。但22 就不是，它可以分成11×2。一些数学家将质数称为构成数学大厦的砖块，你可以通过质数相乘得到其他所有的整数。

下面有几个例子：

55=5×11，

75=3×5×5，

39=3×13，

221=13×17，

31 是质数，

331 是质数，

3331 是质数，

33331 是质数，

333331 是质数，

33333331 是质数，

那么333333331 呢？

它不再是质数了。因为：

17×19607843=333333331。

这就是要告诉我们，永远不要相信表面现象，即便它看上去很像。数学家永远都需要证据。

质数之谜

随便给你一个较大的数字，你怎么知道它是不是质数？质数分布有规律吗？很久以来，数学家们一直在寻找质数出现的规律，但不幸的是，至今也未找到。质数是随机出现在数字当中，没有任何规律的。缺少规律意味着质数只能通过一个一个的试验来寻找。

那怎么找质数呢？两千多年前，希腊数学家埃拉托斯·特尼发明了一种找质数的方法。它好像一个筛子，把合数筛去后，剩下的便是质数了。所以人们就把埃拉托斯·特尼的方法叫作“埃拉托斯特尼筛”，简称“筛法”。

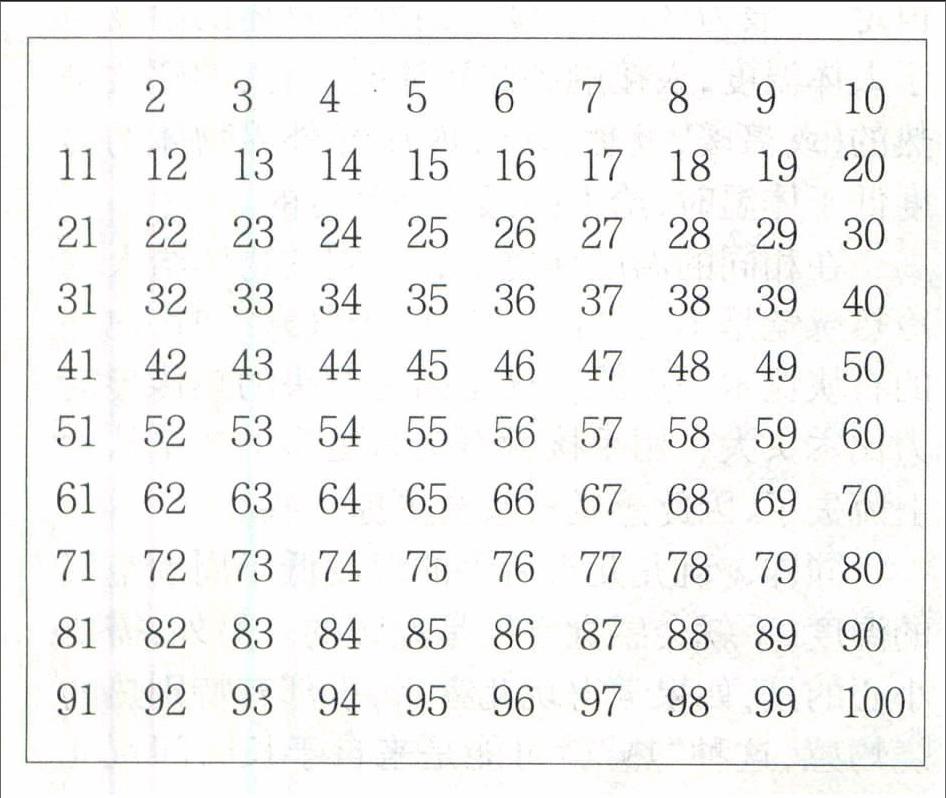
通过“筛法”可以很容易地找到较小的质数。譬如要找101 以内的质数，只需将2—100 的数字写在格子里，不要写1（1 不是质数）。划掉2 的倍数，留下2。划掉3 的倍数，也留下3。这时你可以发现，4 和4 的倍数都已经被划掉，所以接着划掉5 的倍数，然后是7。格子里所有剩下的数字都是质数。

2 3 4 5 6 7 8 9 10

11 12 13 14 15 16 17 18 19 20

21 22 23 24 25 26 27 28 29 30

31 32 33 34 35 36 37 38 39 40

41 42 43 44 45 46 47 48 49 50

51 52 53 54 55 56 57 58 59 60

61 62 63 64 65 66 67 68 69 70

71 72 73 74 75 76 77 78 79 80

81 82 83 84 85 86 87 88 89 90

91 92 93 94 95 96 97 98 99 100

寻找最大的质数

“筛法”对于寻找小的质数很方便，但是对于大的质数呢？ 523367890103 是不是一个质数呢？唯一的办法就是去确认除了1 和它本身，能否再被其他数整除，但是这将耗费大量的时间。尽管如此，数学家们还是找到了一些大得令人吃惊的质数。目前所知道的最大的质数超过780万位。如果用手把它写下来，将会花费7个星期，长度将达到46千米。

如果你想要搜寻最大的质数，你所需做的只是从网络上下载一个程序，剩下的就交给你的计算机来完成。全世界约有4000人正在做这件事。

质数有什么用？

质数有什么用？是的，它既不能吃也不能喝。远在古希腊时代，人们就开始痴迷地研究质数，沉浸于这个几乎没有任何实用价值的思维游戏中。不过到了近代，尤其是计算机诞生之后，对于质数研究的一系列理论突然大放异彩，有了很广泛的用途，譬如将质数应用在数据加密方面。

将几个质数相乘非常简单，但是反过来呢——将一个数分解成质因数相乘的形式是不是很难呢？对于非常大的数字，这几乎是不可能的。因此也就使得质数在设定密码方面相当适合。当你在网上消费的时候，交易的细节都是通过这种方式隐藏起来的。代码的“锁”是非常大的数字，而“钥匙”则是由它的质因数组成的。