例谈一类齐次不等式的解法策略

江苏省扬州大学数学科学学院(225002) 刘铭鑫 濮安山

不等式问题作为高考的热点问题,信息少,难度高,如何在较短的时间内发现规律,从而找到合适的解法策略,一直是众多学生所追求的.从某市最近的几次模考中不难看出,大多数学生在解答有关齐次不等式求最值问题时,方法单一,思路欠缺,得分率较低.笔者通过对近几年齐次不等式解法的探究归纳,以此期望帮助学生对此类问题形成清晰的表象特征,丰富其解题策略,提高其综合解题能力.

策略一 因式分解与换元

例1 已知a,b∈R,满足a2−ab−2b2=1,求a2+b2的最小值____.

其中等号当且仅当

时取得.

分析对于给定的等式,我们要善于从中发现规律,以这种规律作为突破口,建构起解题思路.通过观察,等式的左边可以进行因式分解,并且两个因式的乘积为一个定值,联想到基本不等式中的和积互化,我们进行换元,并且可以将a2+b2反代换成关于x和y的一个表达式,进一步利用基本不等式,原式得到解决.

相关习题

习题1 (2018扬州市二模理科第12题)已知a,b∈R,a＞b,若2a2−ab−b2−4=0,则2a−b最小值为____.

习题2 已知x,y∈R,满足x2−xy+y2=1,求x2−y2的最值___.

策略二 均值缩放

例2 已知x＞0,y＞0,满足4x2−xy+y2=25,求3x2+y2的最大值___.

解由4x2−xy+y2=25得

分析我们知道,利用均值不等式是解决一类不等式的重要方法和途径,而均值不等式是关于所有变元的齐次不等式(整式不等式或等式的所有项的次数相等,或分式不等式的分子、分母所有项的次数都相等).[1]在此基础上观察条件和结论,发现前后所有变元的次数相等,可以进行一次放缩,先将xy构造成有关x2和y2的表达式,但通过尝试我们发现直接利用基本不等式所得到的有关x2和y2的表达式,并非是我们所要求的,因此将原式稍加改变,添加一个参数λ,利用待定系数法,先扩张,再化简,进而利用问题中的倍数关系求出系数,问题得以解决.

相关习题

习题3 已知a＞0,b＞0,a2+2b2=ab+3,求a2+b2的最大值是___.

习题4 已知正实数x、y满足2x2+2y2−xy=1,求3x2+4y2的取值范围是____.

策略三 三角换元

例3 已知4x2−xy+y2=25,求3x2+y2的取值范围是____.

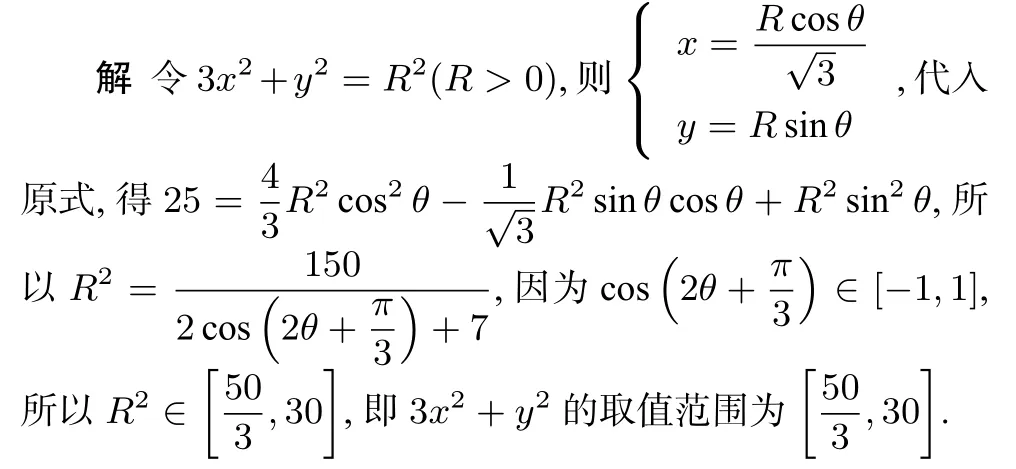
分析通过对原式的观察,发现原式的左边并不能因式分解,故策略一不能使用,对比例二,变元的范围并没有限定,故不满足策略二缩放的要求.回顾题目,这是一道有关平方和的问题,可以抽象拓展到三角函数的平方和上,也就是我们俗称的三角换元法,原式转变为有关R和θ的等式,其中R2可以单独提出来,这也是我们所要求解的,原问题转变为一道三角函数求最值问题,接下来利用三角恒等变换、二倍角公式等,思路逐渐清晰.

相关习题

习题5 已知实数x,y,满足2x2+2y2−xy=1,求3x2+4y2+2xy的取值范围是____.

习题6 若a＞0,b＞0,且4a2+b2=4ab+1,则a2+3b2的最大值为____.

策略四 “1”的代换

例4 (2018年扬州高三期末第13题)已知x＞0,y＞0,且5x2+4xy−y2=3,求12x2+8xy−y2的最小值.

等号当且仅当m=3即时取到.

分析学生在学习三角函数恒等变换时初步接触过“1”的代换,常常通过它来构造出有关正切函数的表达式.类比三角函数,我们推广到更广泛的齐次恒等式,通过代换,同样可以构造出一个形如的分式方程,进而换元,未知量个数减少到一个,分式方程的分子分母未知量最高次数都是二次,因此进行裂项,分离出分子中有关t2的项,进而对剩下的一次项再换元,之后上下同时除以m,一个基本不等式便可以构造出来.在来回代换的过程中,变元的取值范围至关重要,影响到最终能否取到等号,所以一定要来回审视题目,分析清楚.

相关习题

习题7 已知a＞0,b＞0,且a2+2b2=ab+3,则a2+b2的最大值___.

策略五 判别式

例5 已知实数x、y满足2x2+2y2−xy=1,求3x2+4y2取值范围是___.

解设

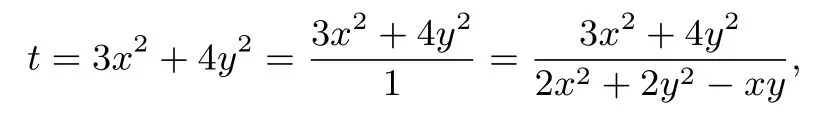
即t(2x2+2y2−xy)=3x2+4y2,化简得(2t−3)x2−tyx+2ty2−4y2=0,因为x要有解,所以∆≥0,即

所以t2−4(2t−3)(2t−4)≥ 0,即(3t−4)(5t−12)≤0,解得所以3x2+4y2的取值范围是

分析判别式法类似于“1”的代换,因为x、y的正负性未知,所以不能直接进行换元求解,联想到函数中根的分布问题,那我们可以将分式中的分母乘到等式左边去,构造成一个关于x的二次函数,因为x的范围是R,故问题转化为等式在R上有解,即关于x的二次函数图象与x轴有交点问题,在计算∆≥0的过程中,发现y2可以提出来,进而转变为求解t2−4(2t−3)(2t−4)≥0,求得的的范围也就是问题所要求的.在这个过程中我们发现y的取值对于解题并没有影响,因此不妨令y=1,这样解题步骤更简洁,思路更明朗.

相关习题

习题8 已知x,y∈R,x2+xy+y2=6,求z=x2+y2的取值范围___.

总结解齐次不等式的题目重在找出变量之间的关系,把握这种关系,并与学生已有的认知结构相关联,架构出合理的解题思路,因此需要学生对必修一到必修五能做到心中有数,理清知识的脉络,教师要重视帮助学生对不等式解题策略进行提炼、总结与反思,并在学生实际完成的情况下,有针对性的强化练习,课堂、课后给足时间让学生进行一题多解的训练,这样,方能做到“以不变应万变”.