两函数公切线问题

云南省玉溪第一中学(653100) 武增明

函数图象的切线问题,一直是高考重点考查的内容,两个函数图象的公切线问题,内涵丰富,是高考命题的一个新热点.这两类问题求解数学思想是一致的,主要是化归与转化思想、函数与方程思想、数形结合思想.求解方法也是一致的,主要是:设出切点,利用切点处的导数即为切线的斜率,利用切点在切线上和曲线上联立方程组求解.但是,两个函数图象的公切线问题要比一个函数图象的切线问题复杂得多,灵活得多,难度大得多.下面笔者通过具体实例,归纳、总结两函数图象的公切线问题的类型及求解思想方法.

设曲线C1:y=f(x)在点A(x1,f(x1))处的切线为l1:y−f(x1)=f′(x1)(x−x1),整理得y=f′(x1)·x−f′(x1)·x1+f(x1).设曲线C2:y=g(x)在点B(x2,g(x2))处的切线为l2:y−g(x2)=g′(x2)(x−x2),整理得y=g′(x2)·x−g′(x2)·x2+g(x2).由于l1与l2是相同的直线,故有x1=g(x2)−g′(x2)·x2.从而可以求出公切线方程.

从上述分析我们还可以看出,曲线C1:y=f(x)与曲线C2:y=g(x)公切线的条数等价于该方程组解的个数.

1 求公切线方程

例1 函数的图象和函数y=3x3的图象的公切线方程为____.

解设两函数图象的公切线的斜率为k,公切线与曲线切于点与曲线y=3x3切于点则所以

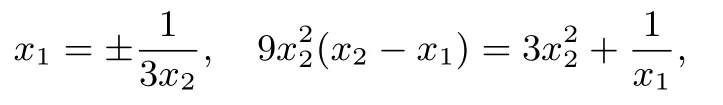
由两函数的图象知,x1与x2同号,即x1x2＞0,所以所以

解得

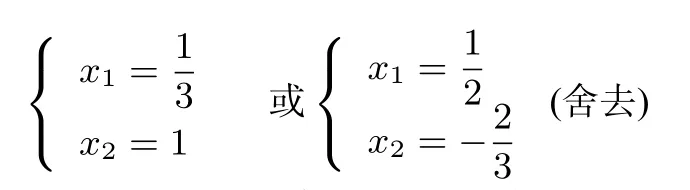
所以k=9,切点为(1,3),所以切线方程为y−3=9(x−1),即9x−y−6=0.

例2 曲线x2=ky与曲线y=lnx的公切线方程为___.

简解

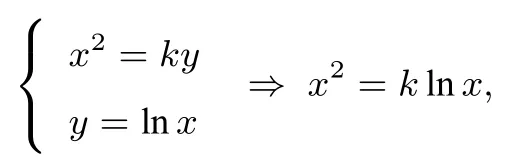
评注(1)若k＞2e,则关于x的方程有两个不等实根,那么两曲线相交,从而两曲线没有公切线(由两函数的图象知),故k=2e.

(2)由上述解答知,两曲线相切,公切线的切点就是两曲线相切的切点.

(4)上述例1的方法对于例2失效!

2 求公切线方程中参数的值

例3 (2016年高考全国卷II理科第16题)若直线y=kx+b是曲线y=lnx+2的切线,也是曲线y=ln(x+1)的切线,则b=____.

解设直线y=kx+b与曲线y=lnx+2相切于点A(x1,lnx1+2).由y=lnx+2 得因此该切线可以表示成整理得同理,设直线y=kx+b与曲线y=ln(x+1)相切于点B(x2,ln(x2+1)).由y=ln(x+1)得因此该切线还可以表示成整理得因此有

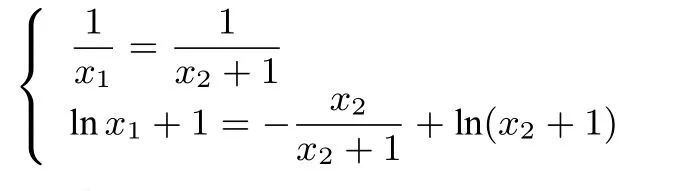
3 确定函数中参数的取值

例4 已知曲线y=x2−lnx在点(1,1)处的切线与曲线y=ax2+(a+2)x+1也相切,则a=____.

解因为曲线y=x2−lnx在点(1,1)处的切线的斜率为1,所以曲线y=x2−lnx在点(1,1)处的切线方程为y=x.因为y=x与曲线y=ax2+(a+2)x+1相切,所以方程ax2+(a+2)x+1=x有一个实数根,即ax2+(a+1)x+1=0有唯一解,故∆ =0,即(a+1)2−4a=0,解得a=1.

例5 已知直线l经过点且与曲线C1:y=x3,C2:y=x2+3x+a均相切,则实数a的值为____.

解设直线l与C1相切于点(x0,y0),而y′=3x2,则切线为它经过点有解得x0=0或x0=1.所以切线为y=0或y=3x−2.由得x2+3x+a=0,∆=9−4a=0,故由得x2+a+2=0,∆=0−4(a+2),所以a=−2,故a的值为或−2.

4 求函数中参数的取值范围

例6 若曲线C1:y=x2与曲线C2:y=aex(a＞0)存在公共切线,则a的取值范围是____.

解设公切线与曲线C1切于点与曲线C2切于点又由曲线C1得y′=2x,曲线C2得y′=aex,所以将aex2=2x1代入化简可得2x2=x1+2.所以因为a＞0,所以x2＞1,记得所以f(x)在(1,2)上递增,在(2,+∞)上递减,所以f(2)是f(x)的最大值,故a的取值范围是

例7 已知曲线y=ex+a与y=(x−1)2恰好存在两条公切线,则实数a的取值范围是()

A.(−∞,2ln2+3) B.(−∞,2ln2−3)

C.(2ln2−3,+∞) D.(2ln2+3,+∞)

解y=ex+a的导数是y′=ex+a,y=(x−1)2的导数是y′=2(x−1).设两条曲线的公切线与曲线y=ex+a相切的切点为(m,n),则n=em+a,与曲线y=(x−1)2相切的切点为(s,t),则t=(s−1)2.公切线的斜率应满足由em+a＞0,可得s＞1.所以由可得所以由2(s−1)=em+a,可得令则由f′(s)＜0,得s＞3,由f′(s)＞0,得 1＜s＜3,所以f(s)在(1,3]上单调递增,在[3,+∞)上单调递减,所以f(s)在s=3处取到最大值f(3)=2ln2−3.若两曲线恰好存在两条公切线,则关于s的方程有两解,所以a＜2ln2−3,所以a的取值范围是(−∞,2ln2−3).故选B.

评注解答此类问题的思路是,从切线重合(即同一条切线)得到两切点的关系,转化所求变量与其中一个切点变量的函数关系,运用化归与转化思想、函数与方程思想,构造函数,并注意函数自变量的范围,通过求导确定函数单调性,运用数形结合思想,得到函数值域也即所求参数的取值范围.

5 求切点横坐标的取值范围

例8 已知函数f(x)=x2的图象在点(x0,x20)处的切线为l,若l也与函数y=lnx,x∈(0,1)的图象相切,则x0必满足()

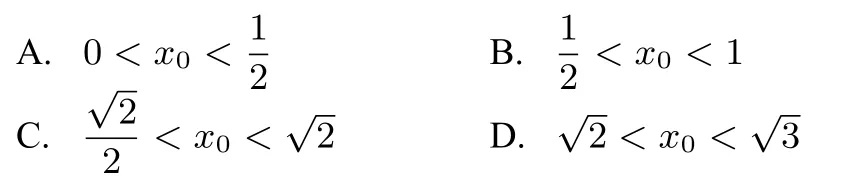
解析由题意,得f′(x)=2x,所以f′(x0)=2x0,所以切线l的方程为

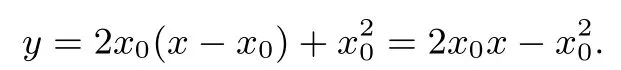
因为l也与函数y=lnx(0＜x＜1)的图象相切,设切点坐标为 (x1,lnx1),易知则切线l的方程为则有又由于0＜x1＜1,所以x0＞1,所以x0∈(1,+∞).令g(x)=x2−ln2x−1,x∈(1,+∞),则所以g(x)在(1,+∞)上单调递增,又所以存在使得g(x0)=0,故选D.

6 判断公切线的条数

例9 已知函数f(x)=x2+2(1−a)x−4a,g(x)=讨论f(x)和g(x)图象的公切线条数.

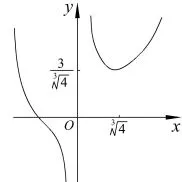
图1

解f′(x)=2x+2(1−a),设公切线与f(x)相切于点A(m,m2+2(1−a)m−4a),则切线方程为

7 探究是否存在公切线

例10 已知函数f(x)=ex,g(x)=lnx是否存在直线l,使得l同时是函数f(x),g(x)的切线?说明理由.

解假设存在直线l同时是函数f(x),g(x)的切线,设l与f(x),g(x)分别相切于点M(m,em),N(n,lnn),则l:y−em=em(x−m)或从而

要讨论l是否存在,只需判定上述方程组是否有解?

例11 设函数

(1)求f(x)的极大值;(2)试探究函数F(x)=x3f′(x)+与函数g(x)的图象在其公共点处是否存在公切线?若存在,研究k的值的个数;若不存在,请说明理由.

解(1)从略.(2)由于

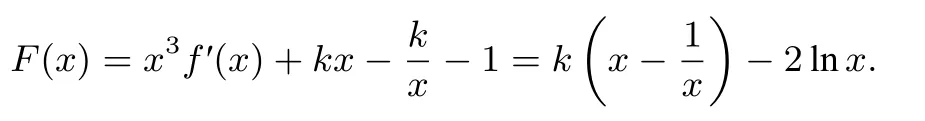
假设函数F(x),g(x)的图象在其公共点(x0,y0)处存在公切线,因为由F′(x0)=即故又函数的定义域为(0,+∞),当k≤ 0时,所以函数F(x)与g(x)的图象在其公共点处不存在公切线.当k＞0时,令即