例谈三角换元法在解题中的运用

广东省广州市第六中学(510300) 璩 斌

三角换元法以三角公式为依托,利用三角函数的性质,将复杂问题移至新对象知识背景中,使复杂的问题简单化,使非标准问题标准化,将问题中分散的条件联系在一起,将问题中隐含的条件显示出来,将问题中的条件与结论联系起来,将抽象的问题转变为具体的问题.

一、解读三角换元法在解题中的运用价值

三角换元法指用一个三角变量代替某个可以看成一个整体的复杂式子,可使问题简化.作为数学解题中的常见的换元技巧,三角换元法利用已知代数值和三角知识中存在的联系进行换元.应用三角换元法将代数函数转变为三角函数,其关键在于构造元与设元,合理的三角换元能够实现化繁为简、化难为易,获得一种简洁优美的解题方法.

三角换元法利用三角函数的有界性,三角函数的性质,三角公式之间的联系等特点,充分利用题设信息,通过联想类比等方式,将高次转化为低次,将分式转化为整式,将超越式转化为代数式,将无理式转化为有理式进行解题.巧妙运用三角换元法解方程、不等式、数列、函数、三角等问题,可以加强数学知识之间的纵横联系,巩固基础知识与基本解题技能,还有助于提高数学运算能力与思维能力.

二、三角换元法在解题中的运用举例

应用三角换元法解决问题时,首先需要将原问题中未知量、未知量代数式等用新的变量进行替换,使原来的数学问题转化为含有新变量的新问题,通过三角换元法实现代数问题向三角函数值域问题的转化,实现化繁为简、化曲为直.

1.巧用三角换元,解根式问题.

应用三角换元法求解本题的关键在于平方关系,将函数化无理式为有理式,从所求式子中巧妙构造出平方和与差为1的式子,根据函数的定义域,就可以给出角的适当范围,将其转化为三角函数在已知区间上的问题进行求解.

例1 求的值域.

方法1 由题意可知,4≤x≤6,当4＜x＜6时,对y=f(x)求导,得

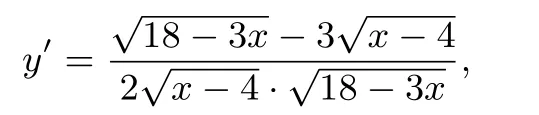
令y′=0解得x=4.5,在[4,4.5)函数单调递增;在(4.5,6]函数单调递减,故当x=4.5时函数取得最大值而当x=4时,时由函数的连续性可知

方法2 分析:利用sin2a=1−cos2a,令x=4+2sin2a进行三角换元去根式.定义域为4≤x≤ 6,设x=4+2sin2a,所以所以当时,y的最大值当时y取最小值

例2 求的值域.

方法1 由题意可得,0≤x≤2,当0＜x＜2时,对y=f(x)求导,得令y′=0解得且在 (0,x1)、(x2,2)处函数单调递减;在(x1,x2)单调递增,因此当x=x1时函数极小值为时函数取得极大值为而当x=0时,y=1;x=2时,y=5,由函数的连续性可知

方法2 分析:由题意令1−x=cosa进行三角换元去根式.

总结在上两道例题中,采用了两种解答方法:方法1是通过对函数求导研究其单调性进而求出函数的值域的,属于高考常用的方法;而方法2则是运用了三角换元法.使用方法1需要先求导解出驻点,再进一步分析出不同区间的单调性进而求出最值,而方法2的三角换元法进行了一次代换以后使用合一公式就可以直接看出最值了,和方法1相比,不仅更容易计算,并且绕过了对单调区间的分析,直接求出了最值.在后面的例题中我们直接介绍使用三角换元法.

例3 如果x,y,z＞1且证明:

分析利用进行三角换元.

证明设且α,β,γ为锐角,则

由已知可得cos2α+cos2β+cos2γ=2,即sin2α+sin2β+sin2γ=1.转化为证明

由柯西不等式可证

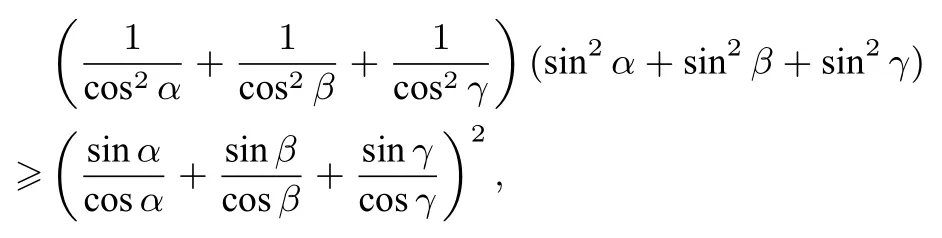
所以原不等式成立.

例4 已知x,y都是正数,且x−y= 1,求证:0＜A＜1.

分析从x−y=1这一特征联想到sec2α−tan2α=1,可以采用三角换元.

证明设x=sec2α,y=tan2α,其中于是

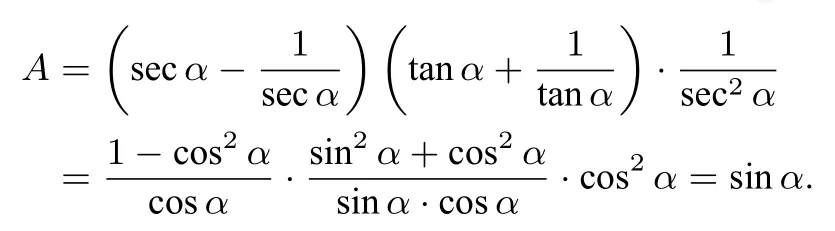
当题中出现x−y=a(x,y,a＞0)时,可设x=asec2α,y=atan2α其中在形如中,可设x=acosα,其中α∈[0,π],或设x=asinα,其中在形如中,可设x=asecα,其中

2.利用三角恒等式换元

主要是通过三角函数恒等变换,使函数关系式转化为三角的函数形式,借助三角换元法来解决,如等.

例5 解方程组

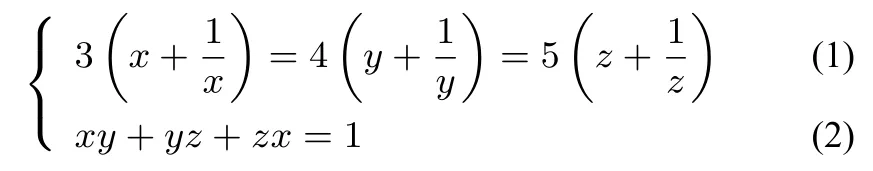
分析由联想到可以采用三角换元法.

解由(1)知x,y,z同号,不妨先考虑它们都是正数的情形,令且α,β,γ∈(0,π),由于

α,β,γ是某个三角形的三个内角,且它的三边之比为3:4:5,勾股数,由上式可知,sinγ=1,从而若x,y,z都是负数,用同样的方法可求得即原方程组的解是

3.应用万能公式进行三角换元

例7 求的最值.

分析函数的解析式可变形为

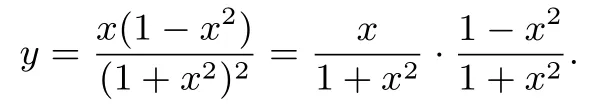
当sin4θ=1时,当sin4θ=−1时,

4.利用两角和与差的正切公式进行三角换元

5.利用三角函数线来换元

例9 已知∠A,∠B,∠C为锐角三角形的三个内角,求证:sinA+sinB+sinC+tanA+tanB+tanC＞2π.

分析若能证明sinA+sinB+sinC+tanA+tanB+tanC＞2(A+B+C)=2π成立即可,由此想到单位圆中的函数线可进行三角换元.

证明如图,设∠A的终边OM与单位圆相交于M,过M作MN⊥Ox,过Q作QP⊥Ox交OM的延长线于P,由三角函数线的知识可得sinA=NM,tanA=QP,∠A= 弧MQ.

图1

下面通过计算面积来证明sinA+tanA＞2∠A.

过M作圆的切线交QP于T,显然,由∠PMT=90°知,PT＞MT=QT,于是S△PMT＞S△MTQ＞S弓形MQ.所以,S△OMQ+S△OPQ＞2S扇形OMQ,故

同理可证sinB+tanB＞2∠B,sinC+tanC＞2∠C,所以sinA+sinB+sinC+tanA+tanB+tanC＞2(A+B+C)=2π.

三、应用三角换元法解题的教学思考

三角换元法解题的精髓在于以“式”换元,引入一个或几个新变量代替原有的某些变量或代数式,利用新的变量求解,然后再返回题目求原变量.类似这样通过引入新元素,将问题中分散的条件相联结或更好的显示隐含条件,或根据等量代换将问题转变为熟悉的知识点.三角换元法的切入点很多,如利用sin2α+cos2α=1,tan2α+1=sec2α,两角和与差的正切公式,万能公式,三角函数线等常见类型进行解题.例如,在处理形如等等时均可考虑进行三角换元.

在教学实践中,还可以适当改变问题的条件、结论等已知信息构建出新的问题.放手让学生尝试运用多种方法解题,大胆对试题条件、结论等进行变式,使学生更好的了解三角换元法及其他解题方法,一道题目因思考角度的不同获得更多的解法,有利于拓宽学生的解题思维.

综上所述,一些高考题、竞赛题往往看起来陌生新奇、颇具深意,但只要加以分析,充分利用已知信息,巧妙应用三角换元法,将复杂代数问题转化为三角问题,可以顺利的解决一些“难题”,对于启迪思维、拓宽视野、提升分析问题和解决问题的能力具有重要意义.