对一道柯西不等式证明题的再次探究

广东省华南师范大学数学科学学院(510631) 李仁旗

柯西不等式的解法研究不仅在高等数学中应用广泛,在中学数学竞赛题中也是时常出现.它的结构独特、对称而优美,学者和研究人员很喜欢使用它.在各种各样的竞赛试题中,如果能够灵活巧妙地使用柯西不等式,那么许多有关不等式的问题,看起来比较复杂,实际上可以迎刃而解.

笔者最近一直在学习和研究柯西不等式,偶然间发现本刊2017年第1期下半月版中《柯西不等式的多种变式及其应用》一文,文中例6的证明过程吸引了笔者的注意力.

(一)例题展示

该例题题目及证明过程如下:

例6 设0≤x≤13,求证:

证明令则a2=x+27,b2=13−x,c2=x,于是有a2+2b2+c2=x+27+2×(13−x)+x=53,原题目可以转化为“已知a2+2b2+c2=53,求a+b+c的最值”问题.构造系数因子有又因为a,b,c≥ 0,所以有a+b+c≤又因为所以有故成立.

(二)定理引入

在剖析本例的解题思路之前,我们先引入柯西不等式:

引理对任意的实数a1,a2,···,an及b1,b2,···,bn有

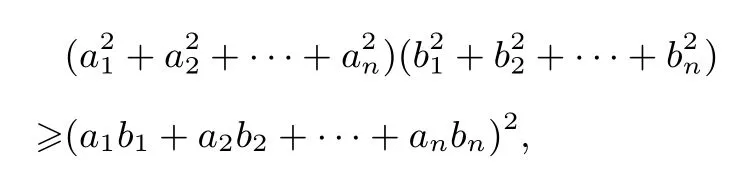
例6中应用到的是三元柯西不等式,即:对任意的实数a1,a2,a3及b1,b2,b3有(a1b1+a2b2+a3b3)2,其中等号当且仅当时成立,其中λ∈R.

(三)例题剖析

了解了柯西不等式的具体内容,我们再来分析一下例6的证明过程.

再来看

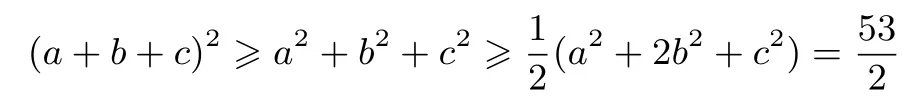
这一步,等号成立的条件是a=c=0,即同样矛盾.即不存在指定范围内x的值满足也就是说结论中的两个等号均不成立.

(四)例题改编

既然如此,笔者认为例6稍作更改可能更为妥当,例题改编如下:

例6 S求函数的最大值和最小值.

解由题知函数y的定义域为[0,13],因为

当x=0时等号成立,故y的最小值为又由柯西不等式得所以y≤11.由柯西不等式成立的条件得4x=9(13−x)=x+27,解得x=9,故当x=9时等号成立,因此y的最大值为11.

(五)点评对比

下面我们就两题的解题思路作一下点评和对比:

(2)应用柯西不等式求最大值时,注意参照变量的系数来凑系数,从而达到消去变量的目的.本例中,观察三个根式可知,三者平方后凑系数时需满足,13−x的系数最大,x的其次,x+27的系数最小.

(3)通过对比可以发现,

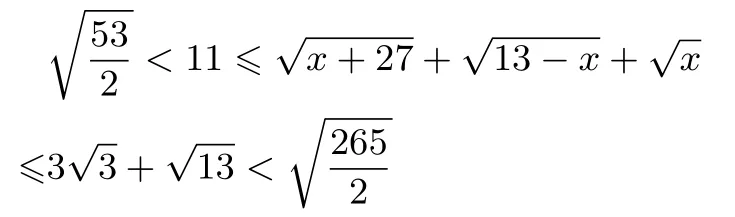
显然,结论

(4)例6S中,应用柯西不等式

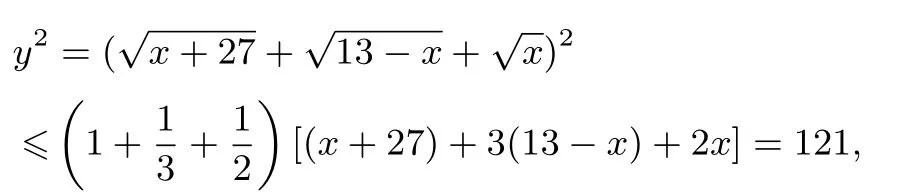
这一步极为巧妙,通过放缩消去变量,同时等号成立时存在对应的x的值.但换一种放缩方法就没有那么“幸运”了,比如:

等号成立时x+27=16(13−x)=9x,显然x无解.

同样是利用放缩法消去未知量,但得到的最大值大于11,并且不存在对应的x的值.那么,在消去变量过程中能不能准确快速的凑系数呢?

(六)深入探究

笔者经过思考,决定如下探究:

设a,b,c＞0,同时结合柯西不等式得

凑系数时应满足

等号成立的条件为

联立(1)(2)得到关于a,b,c,x的四元方程,但只有三个方程式,观察式(2)由x∈[0,13]知,a＜c＜b,不妨令a=1,则有得到一元四次方程

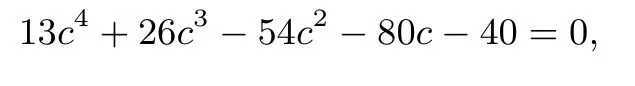
解方程可以得到c=2,于是b=3,x=9,此时y=11,故y≤11.

使用该方法凑系数时引入未知数较多,计算量比较大,涉及到的一元四次方程的解答偏难,具体方法这里就不做介绍.取“a=1”这一步是可行的,凑巧的是计算出b,c,x均为正整数.虽然本例运用柯西不等式可以求出函数的最大值和最小值,但如何快速凑系数确实有难度,因为凑系数后不仅需要消去未知量,更需要检查此时“等号”成立的条件.

柯西不等式及其变式在各种竞赛试题中时常出现,本文就一道例题探究了柯西不等式的一种应用技巧—凑系数.有时为了应用柯西不等式,如何在放缩过程中消去未知量,并且满足柯西不等式“等号”成立的条件?如同本例中的三元柯西不等式一样,直接凑系数虽然来的巧妙,但需要“丰富的想象力”,不然就得用一般化的方法,“待定系数”,然后陷入大量的计算中,毕竟高次方程的解答并非比较简便.

致谢笔者特别需要感谢吴康教授、尤利华教授、钟进均老师在论文写作方面的指导.