待定系数法及其应用拓展

江苏省扬州市田家炳实验中学 宋 扬

一、待定系数法的特征

所谓待定系数法，是指按照实际情况，先设定一个合适的数学表达式，其中含有尚待确定的字母系数，再结合已知条件，得到关于字母系数为未知量的方程或方程组，然后解这个方程（组），从而把问题解出。

所设定的数学表达式通常是一个恒等式，或者是一个函数解析式，其中含有待定的常数（也称系数），习惯上用一些常数字母来表示。

二、待定系数法的来历

1.多项式的恒等变形。

2.函数解析式的确定。

三、待定系数法的理论根据

1.多项式恒等的定义。

2.多项式恒等定理及其推论，包括一元多项式的情形和多元多项式的情形。

四、待定系数法的应用领域

待定系数法应用比较广泛，不仅适用于多项式的恒等变形，还适用于分式乃至一般代数式、一般数学表达式的恒等变形。另一方面，不仅适用于求简单函数的解析式，也可用来确定较复杂函数的解析式。无论是初等数学的变形变式，还是高等数学的积分、级数等运算过程中，都常会用到待定系数法这个有力工具。

五、求待定系数的常用方法和技巧

1.比较系数法，即根据恒等式两边对应项的系数相等，从而进一步求解。

2.赋值法，即对变量取特殊的数值代入并求解。所取的数值，力求使运算简便、快捷。

3.把比较系数和赋值结合起来，灵活运用。

对具体问题，到底采用上述三种方法中的哪一种，要根据具体情况来确定。

六、应用实例解析

例1 如果5x2+kx+7 除以5x-2 余5，求k的值及商式。

解：由于5x2÷5x=x，则根据带余除法可设5x2+kx+7=(5x-2)(x+m)+5，

即5x2+kx+7=5x2+(5m-2)x-2m+5。

所以k=-7，商式为x-1。

例2k为何值时，多项式x2-2xy+ky2+3x-5y+2 能分解成两个一次因式的积？并写出相应的分解式。

解：因为x2+3x+2=(x+1)(x+2)，则可设原式=(x+my+1)(x+ny+2)，

即原式=x2+(m+n)xy+mny2+3x+(2m+n)y+2。

所以当k=-3 时，原多项式能因式分解，其分解式为x2-2xy-3y2+3x-5y+2=(x-3y+1)(x+y+2)。

通分后可得x2+x-3=A(x-2)(x-3)+B(x-1)(x-3)+C(x-1)(x-2)。

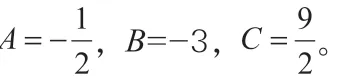
例4 将5x3-6x2+3 按(x-1)的方幂展开。

解：设 原式=5(x-1)3+a(x-1)2+b(x-1)+c，

即原式=5x3+(a-15)x2+(-2a+b+15)x+(a-b+c-5)。

所以原式=5(x-1)3+9(x-1)2+3(x-1)+2。

例5 已知(x2+ax+b)10=(x+5)20-(cx+d)20，求a、b、c、d的值。

解：令x=-5，得(25-5a+b)10=-(-5c+d)20，

从而有d=5c，代入原式得(x2+ax+b)10=(1-c20)(x+5)20。

比较上式两边最高次项(即x20)的系数，得1=1-c20。

于是有c=0，d=5c=0，

原式化为(x2+ax+b)10=(x+5)20=(x2+10x+25)10。

比较两端(括号内)系数得a=10，b=25。

所以，a=10，b=25,c=d=0。

例6 已知实数a,b满足0 ≤a-b≤1，1 ≤a+b≤4，求当a-2b取最大值时，2018a+2019b的值。

解：设恒等式a-2b=m(a-b)+n(a+b)=(m+n)a+(-m+n)b。

此时2018a+2019b=2018。

例7 分解因式(x-y)3+(y-z)3+(z-x)3。

解：设原式=f(x)，即把原式看成关于x的一元多项式，易得f(y)=0。由因式定理知，原式必有因式(x-y)。同理，(y-z)，(z-x)也是原式的因式。又原式是三次多项式，则可设原式=k(x-y)(y-z)(z-x)。

不妨令x=2，y=1，z=0，代入上式两边，即可得k=3，

所以原式=3(x-y)(y-z)(z-x)即为所求。

例8 已知f(x)是一次函数，且f[f(x)]=4x-1，求f(x)的解析式。

解：设y=kx+b，则f[f(x)]=k(kx+b)+b=k2x+(kx+b)=4x-1。