巧妙利用“基本不等式”解决椭圆中三角形面积的最值问题

安徽省宁国中学(242399) 汤生兵

题目1 如图1所示,椭圆C:x2+3y2=3b2(b＞0).

图1

(1)求椭圆的离心率.

(2)若b=1,A,B是椭圆C上两点,且求△AOB面积的最大值.

解(1)略.(2)方法1 (常规解法)若直线AB斜率不存在,即AB⊥x轴时,则若直线AB斜率存在时,设AB方程为y=kx+m,从而

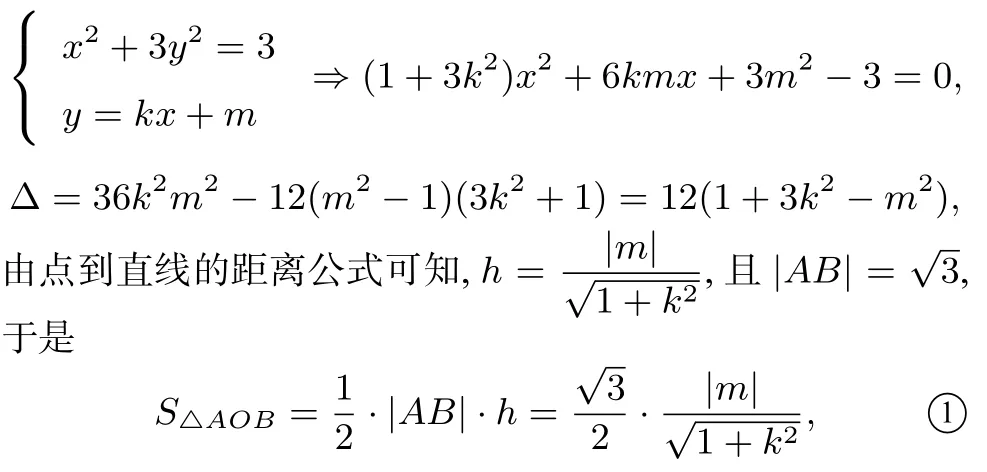
接下来找k和m的关系,因为

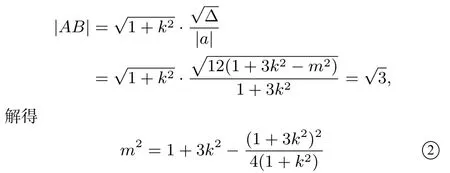
由①,②可知,

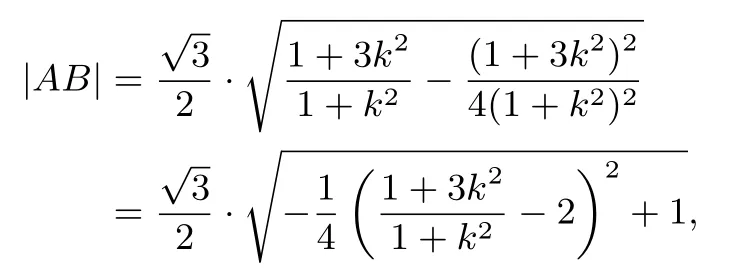
方法2 (基本不等式)

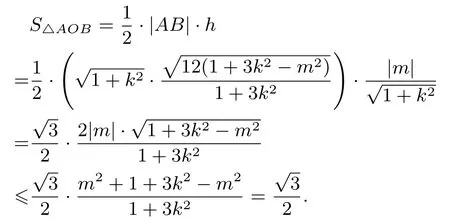
大家不难发现,方法2巧妙利用了基本不等式解决面积最大值,是否存在“巧合”,接下来进行一般化,验证是否仍然可以用.

题目2 已知椭圆点A,B为椭圆上两点,求△AOB面积的最大值.

解若直线AB斜率不存时,设AB=h,则于是

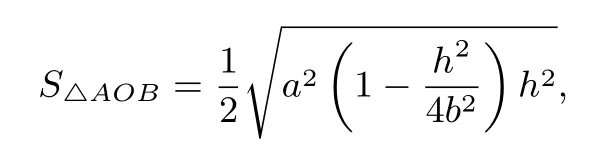
当h2=2b2时,

若直线AB斜率存时,设AB方程为y=kx+m,从而

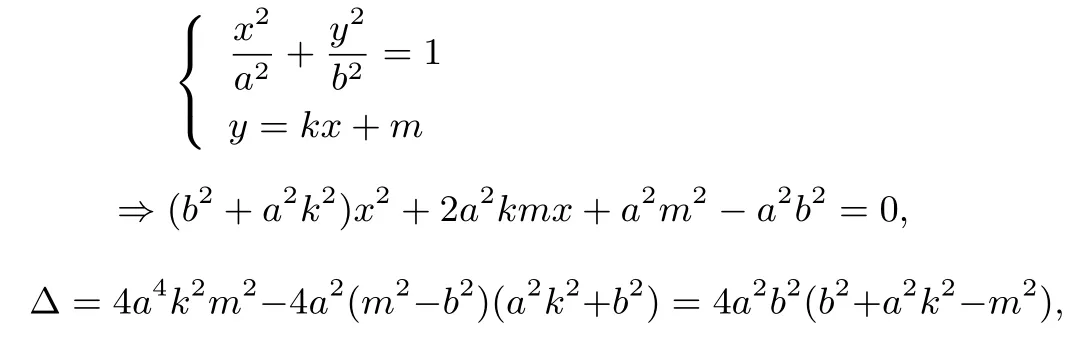
又因为

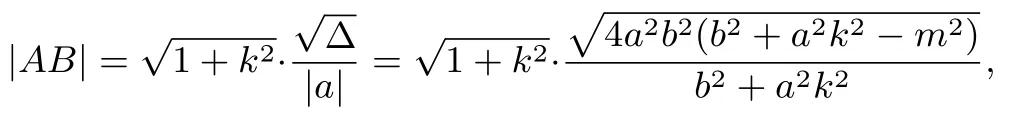
有些学生会感到吃惊,基本不等式很神奇,其实此类题型利用基本不等式有前提条件,即它的分子必须是|m|,才能平方后与后面−m2相互抵消,等价于三角形必须有个顶点在原点,其它情况都不可以用,并且我们得到一个很好的结论S△AOB的最大值为以后遇到小题就可以秒杀,相当的霸气,接下来利用上面结论解决题目3.

题目3 已知椭圆E:点A,B为椭圆上两点,△AOB的面积为设直线OA,OB的斜率分别为k1,k2,求k1·k2的值.

解设A(x1,y1),B(x2,y2),于是

由题目2可知:

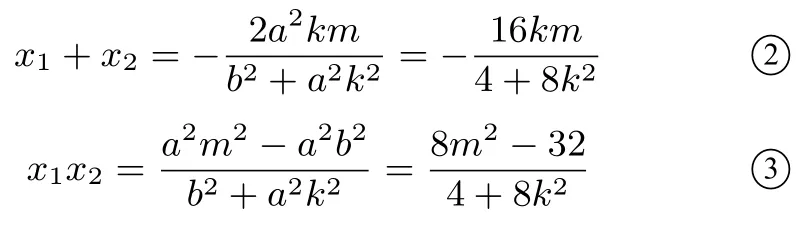
又因为

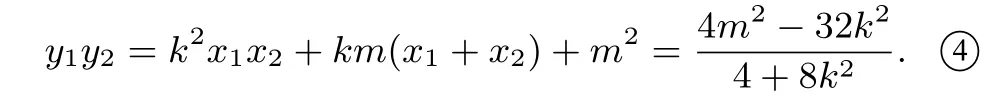
总结通过上面三个题目,只要△AOB有一个顶点为原点,就可以用基本不等式求出它的最大值为若三个顶点都在椭圆上,初等数学很难解决,只能用高等数学将椭圆压缩变换为单位圆去解决,得到最大值为就不一一阐述了.