一道不等式习题的证法探究

湖南省会同县第一中学(418300) 唐鹏久 于先金

题目(《不等式选讲》4-5人教B版第24页练习第3题)已知a,b,c是任意实数,求证:a2+b2+c2≥ab+bc+ca.

这是一个关于a,b,c结构简洁、对称优美、应用广泛的经典不等式,探究这个不等式的证法是一件有意义的工作,并使我们体会到数学的简单美、对称美、和谐美和奇异美.

一、利用重要不等式,感受简单美

所谓简单美,是指一个复杂问题的简单解法.它是优化解题思路的内在驱动力因素之一.正如高斯对自己的工作的评价:“去寻求一种最简的证明,乃是吸引我去研究的主要动力.”也就是说,数学美是指追求最容易、最清楚而且更经济的方法来解题.数学美,美在简单、明了.

证法1 (巧妙配凑,简单明了)因为所以原不等式成立.

证法2 (柯西登场,良性互动)由柯西不等式,得

从而

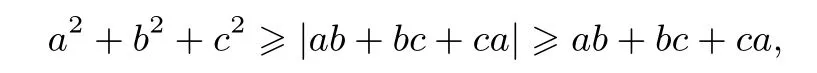
所以原不等式成立.

证法3 (排序原理,意外惊喜)由对称性,不妨假设a≤b≤c,由排序不等式:“顺序和”≥“乱序和”,得

即a2+b2+c2≥ab+bc+ca,故原不等式成立.

二、恒等变形,感受对称美

对称是最能给人以美感的一种形式.正如德国数学家、物理学家魏尔说:“美和对称紧密相关.”对称不外乎局部与局部的对称,几何图形与数学关系都存在这种对称.体现形结构与数(式)结构的对称是对称美,已知与结论的对称使解题者感到愉悦.本题中的条件和结论都关于a,b,c对称,由对称性启发,可得不同的证法.数学美,美在对称、整齐.

证法4 (作差配方,一目了然)因为

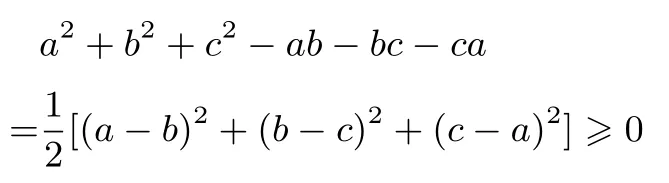
所以原不等式成立.

评注这种作差法,即作差—变形—定号的过程体现了转化与化归的数学思想和数学的对称美.

证法5 (恒等变形,配方分解)由对称性,不妨设a≤b≤c,那么

所以原不等式成立.

证法6 (借行列式,殊途同归)由对称性,不妨设a≤b≤c,那么

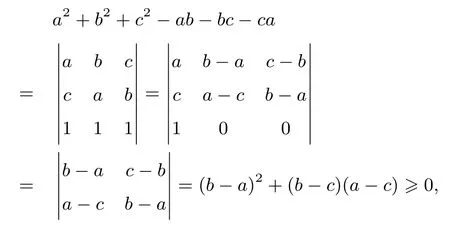
所以原不等式成立.

三、确定主元,感受和谐美

和谐美或称统一美,是指部分与部分之间、部分与整体之间的和谐一致,是指在不同的数学对象或同一对象的不同组成部分之间所存在的内在联系或共同规律.统一性是数学美的重要标志,是数学家不懈追求的永恒目标,也是数学发现与创造的美学方法之一.所以在数学解题中的信息转换、分合并用、进退互化、正反相辅等方面都能畅通无阻,转化为更加协调的形式,化归为已经解决的问题.所以和谐美既是条件与结论的和谐,又是数与形的和谐,更是解题方法与思维策略的和谐,还是数学思想与思维途径的和谐.数学美,美在和谐、统一.

证法7 (为主元,配方显然)因为

所以原不等式成立.

证法8 (构造二次,判别式法)将

视为变量a的二次式,因其判别式

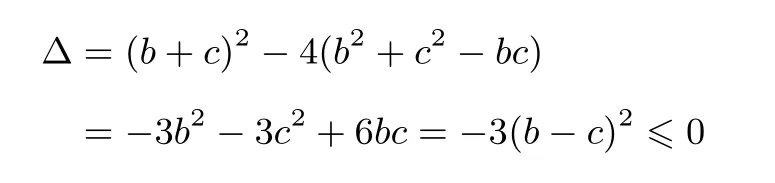
所以a2−(b+c)a+(b2+c2−bc)≥0,故原不等式成立.

证法9 (构造函数,利用导数)由对称性,不妨设a≤b≤c,令

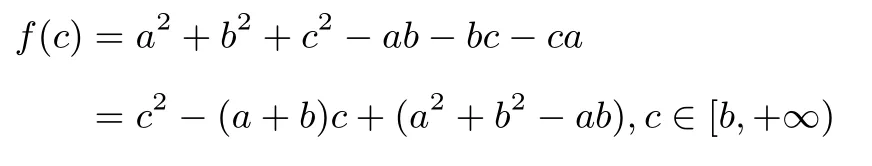
由于f′(c)=2c−(a+b)≥0,于是函数f(c)在区间[b,+∞)上是增函数.由c≥b,f(b)=b2−(a+b)b+(a+b−ab)=a+b−2ab=(a−b)2≥0,得f(c)≥f(b)≥0,所以原不等式成立.

四、证法新颖,感受奇异美

奇异与突变是一种奇特的数学美.奇异美是指所得出的结果新颖、独特、奇特、出人意料,使人感到惊奇、赞赏与折服.徐利治教授说:“奇异是一种美,奇异到极度更是一种美.”在数学解题中,奇异性的存在使得构造反例、寻求特例、反证、极端等手法能够发挥出乎意料的作用,正难则反、以退求进、逆向思维、发散思维等可以认为是对奇异性的通俗理解.数学美,美在奇异、突变.

证法10 (增量换元,柳暗花明)由对称性,不妨设a≤b≤c,令b=a+x,c=a+y,所以由对称性,y≥x≥0.由

所以原不等式成立.

证法11 (构造向量,精彩呈现)令m=(a,b,c),n=(b,c,a),因为|m|·|n|≥m·n,所以故原不等式成立.

证法12 (三角换元,胆大心细)因为

所以不妨设a,b,c≥0.令a2+b2+c2=r2(r≥0),所以可设所以

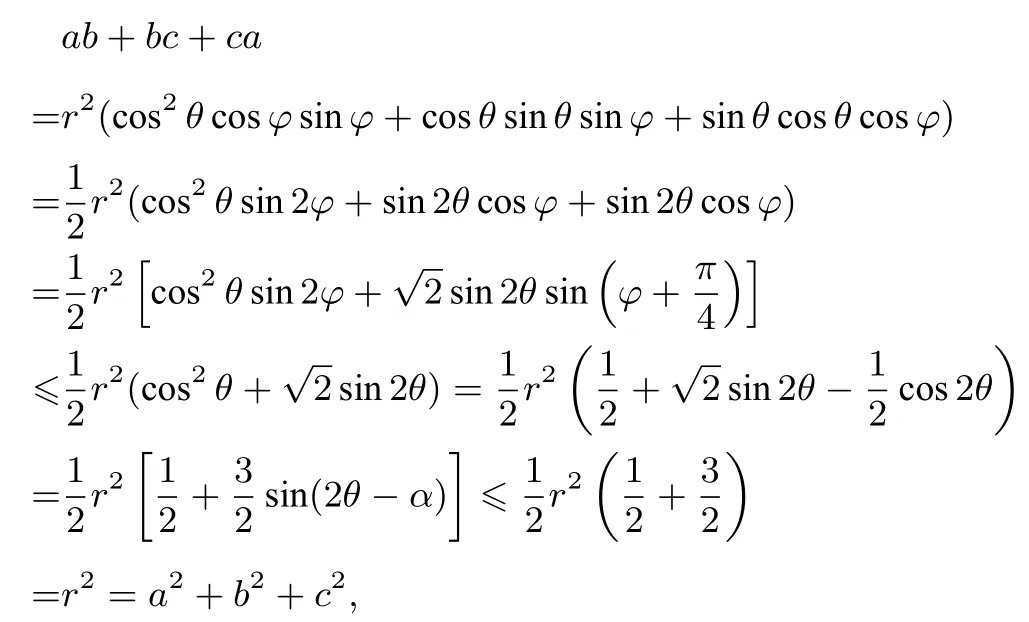
这个不等式的以上证法,真是“横看成岭侧成峰,远近高低各不同”,从不同的视角有不同的证法,各显神通.数学有味,数学好玩.

在数学解题中,数学美能给我们一种认识题意、探求思路、发现解法的新角度、新方法和新思路,因而数学美是探求思路、发现解法的源泉.简单美、对称美、和谐美和奇异美等数学美的各种表现形式在解题中不是孤立的,而是相互结合、相互渗透的.我们不仅要善于发现数学美,而且要自觉运用数学美和追求数学美.